JZOJ 5033. 【NOI2017模拟3.28】A

A

题面

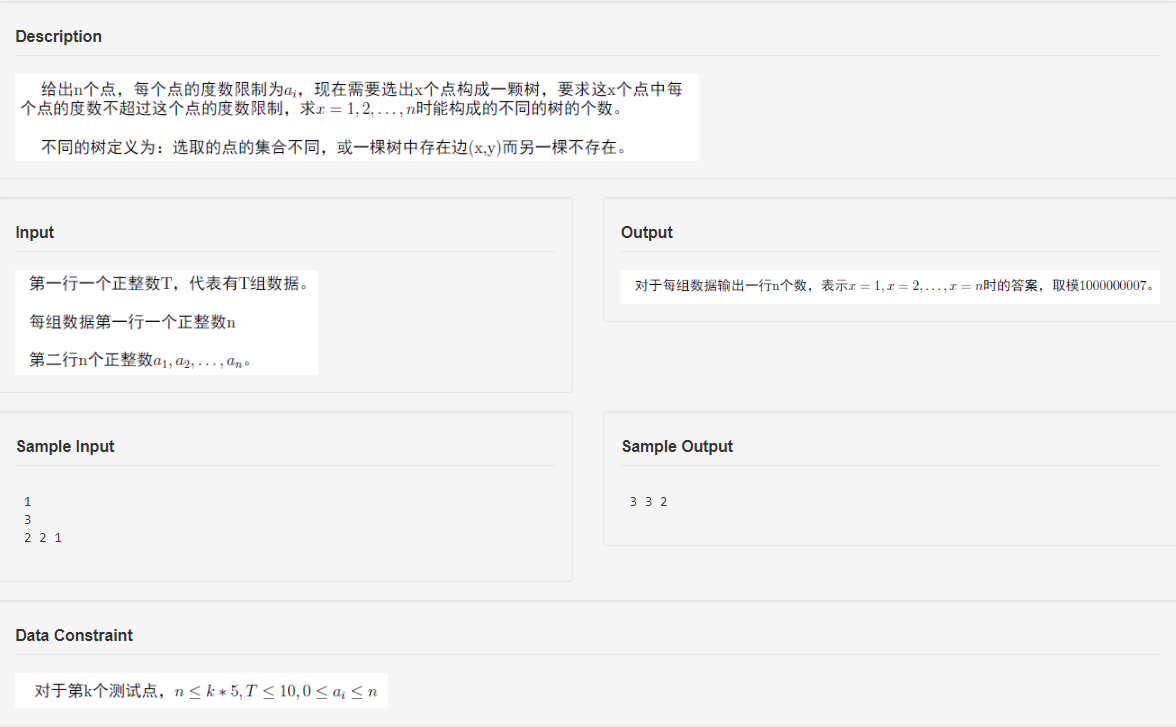
思路

非常抽象地让你构造树，很容易想到 \(prufer\) 序列（如果你会的话）

说明一下：\(prufer\) 序列可以唯一确定一颗树的形态

若树的节点个数为 \(n\)，那么 \(prufer\) 序列长度为 \(n-2\) ，且一个节点出现的个数为它的度数减一（不要问我为什么，因为 \(prufer\) 序列就是这样的）

那么我们就考虑 \(dp\) 了

设 \(f_{i,j,k}\) 表示考虑前 \(i\) 个数，选出 \(j\) 个数，当前 \(prufer\) 序列长度为 \(k\)。

为何要设 \(k\) ？因为一个节点在 \(prufer\) 序列中出现可能不止一次

考虑转移： \(f_{i,j,k} = \sum_{l=1}^{\min(a_i-1,k)}\binom{k}{l}f_{i-1,j-1,k-l}+f_{i-1,j,k}\)

\(f_{i-1,j,k}\) 意思是第 \(i\) 位不选

选的话，\(l\) 枚举选多少个，\(\binom{k}{l}\) 表示选了之后放到序列中的方案数

那么答案如何计算？

\(ans_x=\sum_{j=1}^x\binom{n-j}{x-j}f_{n,j,x-2}\)

意思是考虑 \(prufer\) 序列中数的种数，用 \(j\) 个数凑出长为 \(x-2\) 的序列。

因为叶子节点不会出现在序列中，所以我们再从剩下 \(n-j\) 个数中选出还差的 \(x-j\) 个数

\(Code\)

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
typedef long long LL;

const int N = 55;
const LL P = 1e9 + 7;
LL f[N][N][N] , fac[N];
int a[N] , n , T;

inline LL fpow(LL x , LL y)
{
	LL res = 1;
	while (y)
	{
		if (y & 1) res = res * x % P;
		y >>= 1 , x = x * x % P;
	}
	return res;
}

inline LL C(int n , int m){return fac[n] * fpow(fac[m] * fac[n - m] % P , P - 2) % P;}

int main()
{
	freopen("a.in" , "r" , stdin);
	freopen("a.out" , "w" , stdout);
	fac[0] = 1;
	for(register int i = 1; i <= 52; i++) fac[i] = (i * 1LL * fac[i - 1]) % P;
	scanf("%d" , &T);
	while (T--)
	{
		scanf("%d" , &n);
		for(register int i = 1; i <= n; i++) scanf("%d" , &a[i]);
		memset(f , 0 , sizeof f);
		f[0][0][0] = 1;
		for(register int i = 1; i <= n; i++)
			for(register int j = 0; j <= i; j++)
				for(register int k = j; k <= n - 2; k++)
				{
					f[i][j][k] = f[i - 1][j][k];
					if (j != 0) for(register int l = 1; l <= min(a[i] - 1 , k); l++)
						f[i][j][k] = (f[i][j][k] + f[i - 1][j - 1][k - l] * C(k , l)) % P;
				}
		printf("%lld " , (LL)n);
		LL ans;
		for(register int x = 2; x <= n; x++)
		{
			ans = 0;
			for(register int j = 0; j <= x; j++) ans = (ans + f[n][j][x - 2] * C(n - j , x - j) % P) % P;
			printf("%lld " , ans);
		}
		printf("\n");
	}
}