「JOI Open 2022」Giraffes 题解

设我们将要给出的观感好的排列为 \(q\)，我们希望求出 \(\sum[p_i=q_i]\) 的最大值（这里指不移动的长颈鹿个数）。

结论一：当且仅当左右端点有当前区间最大值或者最小值时条件才能成立。

证明可以考虑反证，此处略去。

据此可以写出 \(O(4^n)\) 暴力，每次枚举当前区间对应值域最大值/最小值填在左端点/右端点处即可。

考虑 DP，可以设计状态 \(f_{l,r,x,y}\) 表示 \([l,r]\) 填了 \([x,y]\)，注意到 \(y\) 不是必需的，暴力转移就可以做到 \(O(n^3)\)。

---

抛开如何优化这个问题不谈，我们来讨论一下上面的结论在平面的等价描述。

在平面标记点 \((i,q_i)\)，考虑一个大小为 \(n\times n\) 的，以 \((1,1)\) 为右下角的正方形，其刚好包括所有被标记的点，那么实际上，结论也就意味着，所有合法的 \(q\) 可以经过「每次去掉正方形一角的点，并且同时缩小正方形至 \((n-1)\times (n-1)\)，使这个正方形包含剩余的点」这个过程使得正方形可以缩减成一个点。

借用官方题解的一张图来描述一下这个过程，如图 \(q=\{6,1,3,2,4,5\}\)：

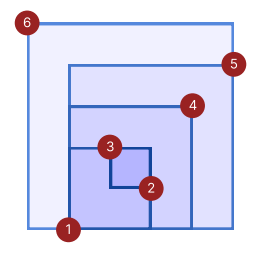
对于原先的排列 \(p\)，就要对于每个 \(q\) 的这个缩减过程，求其不被经过的点的个数的最小值。

那么这个 DP，意味着当前对于某个合法的排列 \(q\)，一个左下角为 \((l,x)\) 边长为 \(r-l+1\) 的合法正方形正要被缩小，而在缩小的过程中我们可以反向构造出 \(q\)。

---

下面我们来讨论一下如何优化这个 DP，首先的第一步是，数据随机是为了什么？

结论二：不被移动的长颈鹿个数不会超过 LIS 和 LDS 大小的总和。

证明：反过来考虑一整个上面的过程可以发现每个合法的 \(q\) 一定可以被拆成一个上升子序列（下文简称 IS）和一个下降子序列（下文简称 DS），具体构造如下：

• 反过来考虑上面的缩减过程，改为扩充。
• 如果扩充左上角或是右下角，将其加入 IS。
• 否则，加入 DS。

贪心的想，既然每个合法的 \(q\) 可以被拆成一个 IS 和一个 DS，那么对于原本的 \(p\)，我们希望固定住尽可能长的 IS 和 DS，即 LIS 和 LDS，而将其他的元素打乱加入 LIS 和 LDS，故 LIS 和 LDS 大小的总和是一个合法上界。

结论三：LIS 和 LDS 的大小在随机情况下是 \(O(\sqrt{n})\) 级别的。

相信这是 Well-Known 的结论，不需要证明，想看证明可以到 Link。

---

据此我们可以知道这样一件事情，我们的 \(f_{l,r,x,y}\) 或者说是 \(f_{l,r,x}\) 的值域是 \(O(\sqrt{n})\) 的，这就引发我们思考是否可以通过换维的方法来优化 DP，当然这是可行的。

改变 DP 状态，记 \(f_{i,j,k}\) 表示，一个以 \((i,p_i)\) 为一角的矩形向四个方向（用 \(j\) 表示），包含至多 \(k\) 个标记点，这个矩形的边长至少是多少。

\(k\) 是 \(O(\sqrt{n})\) 级别的，所以暴力枚举 \(k\)，对于 \(k-1\) 情况下的若干个矩形，如果存在某个矩形位于 \(f_{i,j,k}\) 的转移范围内直接转移即可。

这样子时间复杂度可以到达 \(O(n^2\sqrt{n})\)。

实现可以看 Link，有参考官方题解。

最后一步有两种方向：

1. 注意到转移是类似于「平面上有若干个矩形，询问某个范围内是否有矩形」这样的问题，这是扫描线可以解决的范畴，沿对角线扫描线即可，\(O(n\sqrt{n}\log n)\)，我没写。
2. 修改状态成边长至多是多少，同样这也是等价的，然后每次找矩形保留前若干大的矩形，听起来很离谱，但可能因为随机情况下确实这样可以抵达答案，可以通过。