树形 dp 与树上问题

NFLS 集训笔记 20220802 - 树形 dp 进阶与树上问题综合

\(\text{By DaiRuiChen007}\)

I. 洛谷[P2585] - 三色二叉树

\(\text{Link}\)

思路分析

简单题，建出树后暴力枚举当前节点和其儿子的染色情况，\(dp_{u,c}\) 表示染完 \(u\) 为根的所有子树，且 \(u\) 的颜色是 \(c\) 时的答案，暴力转移即可

时间复杂度 \(\Theta(n)\)

总结：

本题较易，没有什么比较难的坑点，大暴力即可

代码呈现

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=5e5+1,INF=1e18;
int dp[MAXN][3][2],son[MAXN],tot=1;
char tr[MAXN];
vector <int> edge[MAXN];
inline void build(int p) {
	for(int i=1;i<=son[p];++i) {
		edge[p].push_back(++tot);
		build(tot);
	}
}
inline void dfs(int p) {
	for(int v:edge[p]) dfs(v);
	switch(son[p]) {
		case 0: {
			for(int col:{0,1,2}) {
				for(int op:{0,1}) {
					dp[p][col][op]=(col?0ll:1ll);
				}
			}
			break;
		}
		case 1: {
			int u=edge[p][0];
			for(int col1:{0,1,2}) {
				for(int col2:{0,1,2}) {
					if(col1==col2) continue;
					dp[p][col1][0]=min(dp[p][col1][0],dp[u][col2][0]+(col1?0ll:1ll));
					dp[p][col1][1]=max(dp[p][col1][1],dp[u][col2][1]+(col1?0ll:1ll));
				}
			}
			break;
		}
		case 2: {
			int u=edge[p][0],v=edge[p][1];
			for(int col1:{0,1,2}) {
				for(int col2:{0,1,2}) {
					for(int col3:{0,1,2}) {
						if(col1==col2||col2==col3||col3==col1) continue;
						dp[p][col1][0]=min(dp[p][col1][0],dp[u][col2][0]+dp[v][col3][0]+(col1?0ll:1ll));
						dp[p][col1][1]=max(dp[p][col1][1],dp[u][col2][1]+dp[v][col3][1]+(col1?0ll:1ll));
					}
				}
			}
			break;
		}
	}
}
signed main() {
	scanf("%s",tr+1);
	int n=strlen(tr+1);
	for(int i=1;i<=n;++i) son[i]=tr[i]-'0';
	build(1);
	for(int i=1;i<=n;++i) {
		for(int col:{0,1,2}) {
			dp[i][col][0]=INF;
			dp[i][col][1]=-INF;
		}
	}
	dfs(1);
	printf("%lld ",max(dp[1][0][1],max(dp[1][1][1],dp[1][2][1])));
    printf("%lld ",min(dp[1][0][0],min(dp[1][1][0],dp[1][2][0])));
    puts("");
    return 0;
}

---

II. [洛谷3177] - 树上染色

\(\text{Link}\)

思路分析

考虑每条 \(u\to v\) 的边对答案的贡献，设 \(u\) 是 \(v\) 的父亲，且以 \(v\) 为根的子树中选择了 \(x\) 个黑点，则 \(u\to v\) 被计算的次数应该是 \(x\times(k-x)+(siz_v-x)\times[(n-k)-(siz_v-x)]\)

设 \(dp_{u,x}\) 表示以 \(u\) 为根的子树中选择 \(x\) 个黑点，对答案的最大贡献，然后转移的时候枚举每个子节点 \(v\) 内的子结点个数，然后计算 \(u\to v\) 对答案的贡献即可

边界条件： \(u\) 染色或不染色，\(dp_{u,0}=dp_{u,1}=0\)

然后枚举子节点背包转移即可

时间复杂度 \(\Theta(nk^2)\)

总结：

树上背包模板，考虑边的贡献的思路第一次见可能会觉得比较高妙，但再用就会觉得非常基础的一种 trick

状态设计略有不同，注意一下边界条件的处理

代码呈现

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=2001;
int dp[MAXN][MAXN],siz[MAXN],n,k;
struct node {
	int des,val;
};
vector <node> edge[MAXN];
inline void dfs(int p,int f) {
	siz[p]=1;
	dp[p][0]=dp[p][1]=0;
	for(auto e:edge[p]) {
		int v=e.des;
		if(v==f) continue;
		dfs(v,p);
		siz[p]+=siz[v];
		for(int i=min(siz[p],k);i>=0;--i) {
			for(int j=0;j<=min(i,siz[v]);++j) {
				dp[p][i]=max(dp[p][i],dp[p][i-j]+dp[v][j]+e.val*((k-j)*j+(siz[v]-j)*(n-k-(siz[v]-j))));
			}
		}
	}
}
signed main() {
	memset(dp,-0x3f,sizeof(dp));
	scanf("%lld%lld",&n,&k);
	for(int i=1;i<n;++i) {
		int u,v,w;
		scanf("%lld%lld%lld",&u,&v,&w);
		edge[u].push_back((node){v,w});
		edge[v].push_back((node){u,w});
	}
	dfs(1,0);
	printf("%lld\n",dp[1][k]);
	return 0;
}

---

III. [BZOJ2466] - 树

\(\text{Link}\)

思路分析

因为每个节点按/不按都会影响其父亲和儿子的值，所以我们可以设计状态 \(dp_{u,0/1,0/1}\) 表示以 \(u\) 为根的子树，除了 \(u\) 全部点亮，且 \(u\) 没有按/按了，节点 \(u\) 没有亮/亮了的最少方案数

边界条件：\(dp_{u,0,0}=0,dp_{u,1,1}=1,dp_{u,0,1}=\infty,dp_{u,1,0}=\infty\)

然后枚举 \(u\) 的每一个儿子 \(v\) 并转移：

我们以 \(dp_{u,0,0}\) 的转移为例

因为 \(u\) 没有按，所以 \(u\) 的每个儿子都应该是亮的，如果 \(v\) 按了，那么在这之前 \(u\) 应该是亮的，否则 \(u\) 应该是暗的

所以转移如下：

\[dp_{u,0,0}\gets \min(dp_{u,0,0}+dp_{v,0,1},dp_{u,0,1}+dp_{v,1,1})
\]

其他状态的转移类似

时间复杂度 \(\Theta(n)\)

答案为 \(\min(dp_{root,0,1},dp_{root,1,1})\)

注意每次转移 \(dp\) 的时候会更新 \(dp\) 的值，我们要先记录之前的 \(dp\) 值然后转移

总结：

状态设计需要注意只保留与转移有关的状态

注意转移之后更新的数不能影响答案

代码呈现

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int MAXN=101,INF=1e9;
int dp[MAXN][2][2];
//node-id,pressed,lighted
vector <int> edge[MAXN];
inline void dfs(int p,int f) {
	dp[p][0][0]=0,dp[p][1][1]=1;
	dp[p][0][1]=dp[p][1][0]=INF;
	for(int v:edge[p]) {
		if(v==f) continue;
		dfs(v,p);
		int tmp[2][2];
		for(int i:{0,1}) for(int j:{0,1}) tmp[i][j]=dp[p][i][j];
		dp[p][0][0]=min(tmp[0][0]+dp[v][0][1],tmp[0][1]+dp[v][1][1]);
		dp[p][0][1]=min(tmp[0][0]+dp[v][1][1],tmp[0][1]+dp[v][0][1]);
		dp[p][1][0]=min(tmp[1][0]+dp[v][0][0],tmp[1][1]+dp[v][1][0]);
		dp[p][1][1]=min(tmp[1][0]+dp[v][1][0],tmp[1][1]+dp[v][0][0]);
	}
}
signed main() {
	while(true) {
		int n;
		scanf("%lld",&n);
		if(!n) break;
		for(int i=1;i<n;++i) {
			int u,v;
			scanf("%lld%lld",&u,&v);
			edge[u].push_back(v);
			edge[v].push_back(u);
		}
		dfs(1,0);
		printf("%lld\n",min(dp[1][0][1],dp[1][1][1]));
		for(int i=1;i<=n;++i) edge[i].clear();
	}
	return 0;
}

---

IV. [洛谷4037] - 魔兽地图

\(\text{Link}\)

思路分析

树形 dp 高妙题，由于每个物品可能有一些要交给父亲去合成所以不能计入贡献，所以我们可以设 \(dp_{u,k,w}\) 为 \(u\) 物品有 \(k\) 件交给父亲合成，总花费为 \(w\) 的答案

对于叶节点，直接枚举购买量和上交量即可

对于非叶节点，枚举购买量，然后对每种购买量从儿子处转移，要求儿子上交对应量的物品并进行背包，最后枚举上交量更新

时间复杂度 \(\Theta(100nm^2)\)

总结：

状态设计比较巧妙

对于每种购买量都做背包再更新答案

注意转移的顺序和边界条件

代码呈现

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=52,MAXM=2001,INF=1e18;
int dp[MAXN][101][MAXM],f[MAXM],n,m;
/*
 * dp: node-id give-to-father total-cost
 * f: temporary record
 */
int cnt[MAXN],val[MAXN],cost[MAXN],deg[MAXN];
struct node{
	int id,cnt;
};
vector <node> item[MAXN];
inline void DP(int p) {
	if(!p) {
		for(int i=0;i<=m;++i) dp[p][0][i]=0;
		for(auto e:item[p]) {
			int v=e.id;
			DP(v);
			for(int i=m;i>=0;--i) {
				for(int j=0;j<=i;++j) {
					dp[p][0][i]=max(dp[p][0][i],dp[v][0][j]+dp[p][0][i-j]);
				}
			}
		}
		return ;
	}
	if(item[p].empty()) {
		cnt[p]=min(cnt[p],m/cost[p]);
		for(int i=cnt[p];i>=0;--i) {
			for(int j=0;j<=i;++j) {
				dp[p][j][i*cost[p]]=max(dp[p][j][i*cost[p]],(i-j)*val[p]);
			}
		}
		return ;
	}
	cnt[p]=INF;
	for(auto e:item[p]) {
		int v=e.id;
		DP(v);
		cost[p]+=e.cnt*cost[v];
		cnt[p]=min(cnt[v]/e.cnt,cnt[p]);
	}
	cnt[p]=min(cnt[p],m/cost[p]);
	for(int i=cnt[p];i>=0;--i) {
		memset(f,-0x3f,sizeof(f));
		f[0]=0;
		for(auto e:item[p]) {
			int v=e.id;
			for(int j=m;j>=0;--j) {
				int tmp=-INF;
                //先清空再转移
				for(int k=0;k<=j;++k) {
					tmp=max(tmp,f[j-k]+dp[v][i*e.cnt][k]);
				}
				f[j]=tmp;
			}
		}
		for(int j=0;j<=m;++j) {
			for(int k=0;k<=i;++k) {
				dp[p][k][j]=max(dp[p][k][j],f[j]+val[p]*(i-k));
			}
		}
	}
}
signed main() {
	memset(dp,-0x3f,sizeof(dp));
	cin>>n>>m;
	for(int i=1;i<=n;++i) {
		cin>>val[i];
		char op;
		cin>>op;
		if(op=='A') {
			int c;
			cin>>c;
			while(c--) {
				int id,x;
				cin>>id>>x;
				item[i].push_back((node){id,x});
				++deg[id];
			}
		} else cin>>cost[i]>>cnt[i];
	}
	for(int i=1;i<=n;++i) if(!deg[i]) item[0].push_back((node){i,0});
	DP(0);
	int res=-INF;
	for(int i=0;i<=m;++i) res=max(res,dp[0][0][i]);
	cout<<res<<'\n';
	return 0;
}

---

V. [洛谷4649] - 训练路径

\(\text{Link}\)

思路分析

反面考虑，计算最多能加几条非树边使图上没有偶环

如果某条非树边 \((u,v)\) 添加后使得 \(u\to \operatorname{LCA}(u,v)\to v\to u\) 的长度为偶数，则不能必选择 \((u,v)\)

只考虑添加 \((u,v)\) 使得 \(u\to \operatorname{LCA}(u,v) \to v\to u\) 的长度为奇数的边 \((u,v)\)

如果两条边 \((u,v)\) 和 \((x,y)\) 的树上路径有交集，如下图所示，也会形成一个偶环：

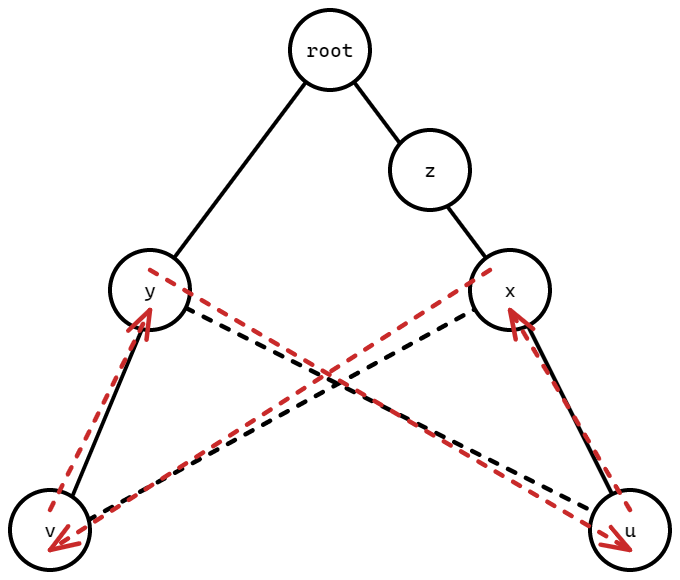
所以我们的目标就是在树上调价若干条不相交的非树边使得其权值和最大

考虑在添加某条非树边 \((u,v)\) 后把 \(u\to v\) 的所有边都删掉，然后分成若干棵子树进行 dp

我们把每条非树边 \((u,v)\) 在 \(\operatorname{LCA}(u,v)\) 处考虑，设 \(dp_{p,\mathbf S}\) 表示以 \(u\) 为根的子树，且 \(p\) 到集合 \(\mathbf S\)（状态压缩）中的儿子的边已经被删掉后能选择的最优答案

那么对于一条路径 \((u,v)\) 满足 \(\operatorname{LCA}(u,v)=p\) 他能带来的价值为：

\[value(u,v)=w(u,v)+\sum_{x\in path(u,v)}^{fa(x)\neq p,x\neq p} dp_{fa(x),\{x\}}
\]

设 \(u\to v\) 的路径包含 \(x\to p\to y\) 且 \(x,y\) 均为 \(p\) 的儿子，我们可以用用这个价值去转移：

\[\forall \mathbf S:x,y\not\in \mathbf S\\
dp_{p,S}\gets value(u,v)+dp_{p,\mathbf S\cup\{x,y\}}
\]

最终的答案为 \(\sum w(u,v)-dp_{1,\varnothing}\)

时间复杂度 \(\Theta(m\log n+n2^{|\mathbf S|})\)

总结：

神仙题

观察性质转化成生成仙人掌

然后状压树上 dp

很强

代码呈现

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1001;
vector <int> tree[MAXN];
struct node {
	int src,des,val;
};
vector <node> vec,link[MAXN];
int dep[MAXN],fa[MAXN],siz[MAXN],son[MAXN],root[MAXN],fid[MAXN];
int dp[MAXN][1<<10];
inline int bit(int x) {
	return 1<<x;
}
inline void init1(int p,int f) {
	fa[p]=f,siz[p]=1,dep[p]=dep[f]+1;
	for(int v:tree[p]) {
		if(v==f) continue;
		init1(v,p);
		siz[p]+=siz[v];
		if(siz[v]>siz[son[p]]) son[p]=v;
	}
}
inline void init2(int p,int r) {
	root[p]=r;
	if(son[p]) init2(son[p],r);
	for(int v:tree[p]) {
		if(v==son[p]||v==fa[p]) continue;
		init2(v,v);
	}
}
inline void init3(int p) {
	for(int i=0;i<tree[p].size();++i) {
		int v=tree[p][i];
		if(v==fa[p]) continue;
		fid[v]=bit(i);
		init3(v);
	}
}
inline int LCA(int u,int v) {
	while(root[u]!=root[v]) {
		if(dep[root[u]]<dep[root[v]]) swap(u,v);
		u=fa[root[u]];
	}
	return dep[u]>dep[v]?v:u;
}
inline void dfs(int p) {
	for(int v:tree[p]) {
		if(v==fa[p]) continue;
		dfs(v);
	}
	for(int s=0;s<bit(tree[p].size());++s) {
		for(int i=0;i<tree[p].size();++i) {
			if(!((s>>i)&1)) dp[p][s]+=dp[tree[p][i]][0];
		}
	}
	for(auto e:link[p]) {
		int val=e.val,u=0,v=0;;
		if(e.src!=p) {
			val+=dp[e.src][0];
			for(u=e.src;fa[u]!=p;u=fa[u]) val+=dp[fa[u]][fid[u]];
		}
		if(e.des!=p) {
			val+=dp[e.des][0];
			for(v=e.des;fa[v]!=p;v=fa[v]) val+=dp[fa[v]][fid[v]];
		}
		int t=fid[u]|fid[v];
		for(int s=0;s<bit(tree[p].size());++s) {
			if(!(s&t)) dp[p][s]=max(dp[p][s],val+dp[p][s|t]);
		}
	}
}
signed main() {
	int n,m,res=0;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;++i) {
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		if(!w) {
			tree[u].push_back(v);
			tree[v].push_back(u);
		} else {
			res+=w;
			vec.push_back((node){u,v,w});
		}
	}
	init1(1,0);
	init2(1,1);
	init3(1);
	for(auto e:vec) {
		int lca=LCA(e.src,e.des);
		if(!((dep[e.src]+dep[e.des]-dep[lca]*2)&1)) link[lca].push_back(e);
	}
	dfs(1);
	printf("%d\n",res-dp[1][0]);
	return 0;
}

---

VI. [洛谷4381] - 岛屿

\(\text{Link}\)

思路分析

显然，本题建图之后会形成一棵基环树森林，题意就是求若干棵基环树的直径之和

基环树的路径只有两种，经过环上边的和不经过环上边的

不经过环上边的可以通过以环上每个节点为根做一次树形 dp 求得，同时记录出每个点 \(u\) 向环外最远能拓展多少的路径的长度 \(dp_u\)

考虑经过环的直径，其形态一定是：过 \(u\) 的环外最长链 \(\to\) 环上 \(u\) 到 \(v\) 的距离 \(\to\) 过 \(v\) 的最长链

那么这段距离的长度为：

\[dp_u+dis(u,v)+dp_v
\]

考虑破环为链然后做一次前缀和用 \(sum_i\) 示第 \(1\) 个点到第 \(i\) 个点的距离

设环的长度为 \(x\)，则我们要求的答案应该是：

\[\text{Answer}=\max_{u,v\in[1,2x]}^{v-u<x}\{dp_u+dp_v+sum_v-sum_u\}
\]

考虑把 \(u,v\) 拆开：

\[\text{Answer}=\max_{v=1}^{2x}\left\{dp_v+sum_v+\max_{u=v-x+1}^{v-1} \{dp_{u}-sum_u\}\right\}
\]

所以我们只需要枚举 \(v\) 然后以 \(dp_u-sum_u\) 维护一个递减的单调队列即可

时间复杂度 \(\Theta(n)\)

总结：

先处理环外直径显然，考虑将环上问题抽象出来是解题的瓶颈，如果能够看出来问题本质或者想到拆环为链，那么列出式子和单调队列优化都非常显然

处理基环树问题的时候，可以考虑拆换为链然后转成数列问题

代码呈现

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e6+1;
struct node {
	int val,des,id;
	node() { val=des=id=0; }
	node(int _val,int _des,int _id) { val=_val,des=_des,id=_id; }
}	sk[MAXN];
vector <node> edge[MAXN];
int dp[MAXN],lst[MAXN],cir[MAXN],x,top,sum[MAXN<<1],w[MAXN<<1],q[MAXN<<1],tot,chain,ans;
bool vis[MAXN],get_circle;
inline void find_circle(int p,node l) {
	vis[p]=true;
	sk[++top]=l;
	for(auto e:edge[p]) {
		if(e.id==l.id) continue;
		int v=e.des;
		if(vis[v]) {
			if(get_circle) continue;
			int t;
			get_circle=true;
			do {
				t=sk[top].des;
				lst[t]=sk[top].val;
				cir[++x]=t;
				--top;
			} while(t!=v&&top);
			lst[v]=e.val;
			continue;
		}
		find_circle(v,e);
	}
	if(!get_circle) --top;
}
inline void dfs(int p,int f) {
	vector <int> vec;
	for(auto e:edge[p]) {
		int v=e.des;
		if(v==f||lst[v]) continue;
		dfs(v,p);
		vec.push_back(dp[v]+e.val);
	}
	sort(vec.begin(),vec.end(),greater<int>());
	if(vec.size()) dp[p]=vec[0],chain=max(chain,vec[0]);
	if(vec.size()>1) chain=max(chain,vec[0]+vec[1]);
}
inline int calc(int u) {
	int r=(u%x+x)%x;
	if(!r) return x;
	else return r;
}
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	int n;
	cin>>n;
	for(int i=1;i<=n;++i) {
		int x,w;
		cin>>x>>w;
		edge[i].push_back((node){w,x,i});
		edge[x].push_back((node){w,i,i});
	}
	for(int i=1;i<=n;++i) {
		if(!vis[i]) {
			get_circle=false;
			top=x=chain=0;
			node st(0,i,0);
			find_circle(i,st);
			for(int i=1;i<=x;++i) dfs(cir[i],0);
			for(int i=1;i<=x*2;++i) {
				w[i]=dp[cir[calc(i)]];
				sum[i]=sum[i-1]+lst[cir[calc(i-1)]];
			}
			int head=1,tail=0;
			for(int i=1;i<=x*2;++i) {
				while(head<=tail&&q[head]<=i-x) ++head;
				if(head<=tail) chain=max(chain,w[i]+w[q[head]]+sum[i]-sum[q[head]]);
				while(head<=tail&&w[q[tail]]-sum[q[tail]]<=w[i]-sum[i]) --tail;
				q[++tail]=i;
			}
			ans+=chain;
		}
	}
	printf("%lld\n",ans);
	return 0;
}

---

VIII. [UOJ#11] - ydc 的大树

\(\text{Link}\)

思路分析

显然，本题中的白色叶节点都可以删去，直到只留下黑色叶节点

考虑树的一个性质：树上所有点到其他节点的最长路一定经过树的中心（直径中点）

因此考虑在当前的树中找到直径中点，把这个节点提到根，此时所有黑节点到他的朋友就一定要过根

然后枚举某个白色节点 \(u\)，显然，以 \(u\) 为根的子树一定会不高兴

然后考虑切掉 \(u\) 的子树会不会让外部其他的点不高兴，将切掉根形成的若干个连通块称为若干个分支

计算出每棵子树中包含的最长链，如果 \(u\) 所在的子树包含其分支中所有的最长链，那么其他分支中的点可能就要过 \(u\) 去找好朋友

• 如果 \(u\) 所在的分支独占了这整棵树中的所有最长链，那么其他所有的点都要经过 \(u\) 去找好朋友，这些点都会不高兴

• 如果 \(u\) 所在的分支占领了这棵树中的最长链，或者 \(u\) 独占了这棵树中的次长链，但这棵树中有且仅有另一个分支中有最长链，那么那个包含最长链分支中的节点都过必须 \(u\) 来找好朋友

枚举每个 \(u\) 处理，时间复杂度 \(\Theta(n)\)

总结：

遇到树上全源最长路，提树的中心到根是一个好想法

剩下枚举分支统计贡献的方式比较 trivial，核心还是转化成过根路径，只统计跨分支贡献

代码呈现

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+1,INF=1e9;
struct node {
	int des,val;
};
vector <node> edge[MAXN];
int fa[MAXN],col[MAXN],siz[MAXN],dis[MAXN],cnt[MAXN],head[MAXN];
int vertex,n,m;
inline void diameter(int p,int f,int d) {
	fa[p]=f,dis[p]=d;
	if(col[p]&&dis[p]>dis[vertex]) vertex=p;
	for(auto e:edge[p]) {
		int v=e.des;
		if(v==f) continue;
		diameter(v,p,d+e.val);
	}
}
inline void dfs(int p,int f,int d) {
	siz[p]=col[p]?1:0;
	cnt[p]=col[p]?1:0;
	dis[p]=col[p]?d:0;
	for(auto e:edge[p]) {
		int v=e.des;
		if(v==f) continue;
		head[v]=f?head[p]:v;
		dfs(v,p,d+e.val);
		siz[p]+=siz[v];
		if(dis[v]>dis[p]) dis[p]=dis[v],cnt[p]=cnt[v];
		else if(dis[v]==dis[p]) cnt[p]+=cnt[v];
	}
}
signed main() {
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;++i) {
		int u;
		scanf("%d",&u);
		col[u]=1;
	}
	for(int i=1;i<n;++i) {
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		edge[u].push_back((node){v,w});
		edge[v].push_back((node){u,w});
	}
	diameter(1,0,0);
	diameter(vertex,0,0);
	int length=dis[vertex],root=vertex;
	while(vertex) {
		if(max(dis[vertex],length-dis[vertex])<=max(dis[root],length-dis[root])) {
			root=vertex;
		}
		vertex=fa[vertex];
	}
	dfs(root,0,0);
	int firlen=0,seclen=0;
	int fircnt=0,seccnt=0,maxtot=0;
	for(auto e:edge[root]) {
		int v=e.des;
		if(!siz[v]) continue;
		if(dis[v]>firlen) {
			seclen=firlen;
			seccnt=fircnt;
			firlen=dis[v];
			fircnt=1;
			maxtot=siz[v];
		} else if(dis[v]==firlen) {
			++fircnt;
			maxtot+=siz[v];
		} else if(dis[v]>seclen) {
			seccnt=1;
			seclen=dis[v];
		} else if(dis[v]==seclen) ++seccnt;
	}
	int ans=0,tot=0;
	for(int i=1;i<=n;++i) {
		if(col[i]) continue;
		int res=siz[i],up=head[i];
		if(i!=root&&dis[i]==dis[up]&&cnt[i]==cnt[up]) {
			if(dis[i]==firlen&&fircnt==1) res+=m-siz[up];
			else if(dis[i]==firlen&&fircnt==2) res+=maxtot-siz[up];
			else if(dis[i]==seclen&&fircnt==1&&seccnt==1) res+=maxtot;
		}
		if(res>ans) ans=res,tot=1;
		else if(res==ans) ++tot;
	}
	printf("%d %d\n",ans,tot);
	return 0;
}