【説明する】hash

首先对于判重，我们能想到的方法有什么呢?

1)bool数组

2)set(集)

数组与集合的优缺点：

1.因为集合是对数组做的封装,所以,数组永远比任何一个集合要快。

2.数组声明了它容纳的元素的类型，而集合不声明。这是由于集合以object形式来存储它们的元素。

3.一个数组实例具有固定的大小，不能伸缩。集合则可根据需要动态改变大小。

4.数组是一种可读/可写数据结构－－－没有办法创建一个只读数组。

3)map(映射)  

4)hash    

因为数组，set，map的适用范围是比较小的，而且速度很慢，

所以今天我们就来研究一下hash~

哈希算法

回忆八数码问题：判重，给定一个九位数，怎么判断有没有在前面出现过？

考虑一种压缩数组的方法：如果我们想要把数组大小变为 N，那么对于一个数 X，存储在 X%N 的位置里面。

这样可以完美解决空间问题。

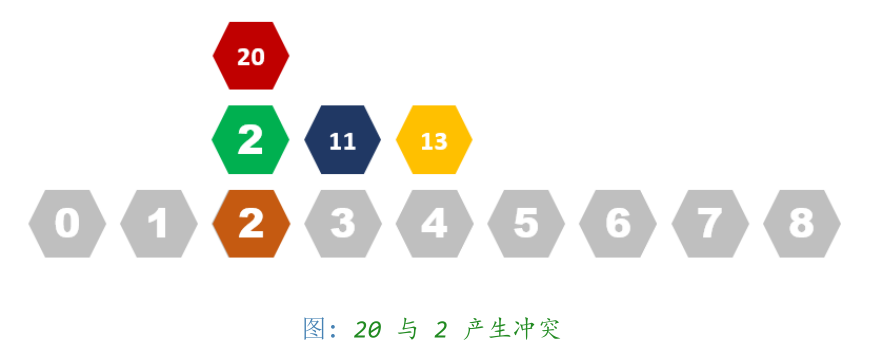
 哈希算法 - 冲突

但存在一种情况：两个数 X 计算到了同一个位置（X%N = Y%N）

模数的确定：  

　　　　取比元素个数大的质数
 该如何解决？

 第一种解决方式：顺序寻址法。
 一直往后查询位置，直到有空为止。

哈希算法 - 判断

那么如何判断这个数是否在之前已经出现过了呢？

类比插入过程，一直往后查询位置，直到出现两种情况之一。
-1 有空位：那就没出现过
-2 查询到一个相等的数：说明已经出现过了

哈希算法 - 顺序寻址法 - 代码实现

int hash_table[N]; // hash_table 哈希表：0 位置代表没有数
void push1(int x)
{
    int y = x % N; // 计算初始位置，N：表的大小
    for(; hash_table[y] && hash_table[y]!=x; ) y = (y+) % N;
    // 寻找到一个 0 位置，或者找到自己为止
    if(hash_table[y]) cout << x << " has␣occured␣before!" << endl;
    // 如果是自己本身，则之前已经出现过了
    else
    {
        hash_table[y] = x; // 否则，将 x 加入表中
        cout << x << " inserted." << endl;
    }
}

哈希算法 - 冲突 - 解决的另一种方式

但存在一种情况：两个数 X 计算到了同一个位置（X%N = Y%N）
 另一种解决方案：把所有数堆到一起（也就是用链表将模数相同的都连起来）

哈希算法 - 链地址法 - 代码实现

// 方法二：链地址法
vector<int> hash_array[N]; // hash_array：每个位置用一个 vector 来维护
void push2(int x)
{
　　int y = x % N; // 计算初始位置
　　for(int i=; i<hash_array[y].size(); i++)
　　if(hash_array[y][i] == x) // 如果之前已经出现过了
　　{
　　　　cout << x << " has␣occured␣before!" << endl;
　　　　return; // 标记已经出现过
　　}
　　// 如果之前没有出现过，将 x 加入表中
　　hash_array[y].push_back(x);//vector加入操作
　　cout << x << " inserted." << endl;
}

字符串哈希

十进制表示法——需要计算出所有前缀所代表的数字。

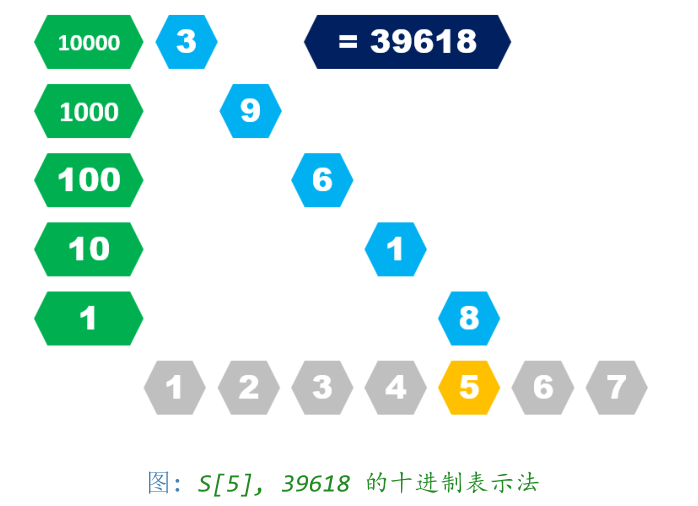
上图，在S[5]存的是39618，S[4]存的是3961，S[3]存的是396，S[2]存的是96，S[1]存的是6

假如需要计算区间 [l,r]所代表的数字 X，有
    X = S[r] − S[l − 1] × 10 r−l+1

字符串哈希 - 联系

那么问题来了:数字和字符串有什么联系吗？

其实我们可以把一个字符串看作是一个特殊的数字：

对于字符串“ABABC”，我们定义它的哈希值 H 为：H = ”A” ∗ D^4 + ”B” ∗ D^3 + ”A” ∗ D^2 + ”B” ∗ D + ”C”

- 其中 D 为一个规定的数。

D在字符串全为大写或者全为小写时，范围是26~27，当字符串中既有大写又有小写时，取52

那么我们可以把字符串看作是一个D 进制的数。计算方法和数字是类似的，而且对于相同字符串，得到的结果是相同的。

字符串算法 - 代码实现

string s; // s 为字符串
int f[N], g[N]; // f 为前缀和，g[i] 为 D 的 i 次方
void prehash(int n) // 预处理哈希值
{
　　// 预处理时，注意到数字可能很大，对一个数 MD 取模
　　f[] = ; // f 前缀和预处理
　　for(int i=; i<=n; i++) f[i] = (1LL * f[i-] * D + s[i-]) % MD;
　　g[] = ; // g：D 次方预处理
　　for(int i=; i<=n; i++) g[i] = 1LL * g[i-] * D % MD;
}
int hash(int l, int r) // 计算区间 [l,r] 的哈希值
{
　　int a = f[r];
　　int b = 1LL * f[l-] * g[r-l+] % MD; // 记得乘上次方
　　return (a - b + MD) % MD; // 前缀和相减
// 有可能结果小于 0，加上一个 MD 将其变为正数
}
if(hash(a, b) == hash(c, d)) // 这就说明字符串 [a,b] 与字符串 [c,d] 匹配

字符串算法 - 几点注意事项

哈希算法：数组长度 N 用质数，减少冲突的次数，增加效率

字符串哈希：因为只是用一个小于 MD 的数来代表一个字符串，也是一种哈希；所以有可能会产生冲突(不同的字符串有相同的数)，

- 可以通过前面的方法来解决：设哈希表(但速度很慢)。
- 解决方式：用质数来减少冲突的可能性；用几组不同的 D 与 MD。

// 哈希算法: N 使用质数
const int N = ;
// 字符串哈希: 多用质数，不容易产生冲突
const int D = ; const int MD = 1e9 + ;
// 用几组不同的 D 与 MD
const int D2 = ; const int MD2 = 1e9 + ;

End.