【luoguP1955 】[NOI2015]程序自动分析--普通并查集

题目描述

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设x1,x2,x3...代表程序中出现的变量，给定n个形如xi=xj或xi≠xj的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：x1=x2,x2=x3,x3=x4,x4≠x1，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

输入格式

从文件prog.in中读入数据。

输入文件的第1行包含1个正整数t，表示需要判定的问题个数。注意这些问题之间是相互独立的。

对于每个问题，包含若干行：

第1行包含1个正整数n，表示该问题中需要被满足的约束条件个数。接下来n行，每行包括3个整数i,j,e，描述1个相等/不等的约束条件，相邻整数之间用单个空格隔开。若e=1，则该约束条件为xi=xj；若�e=0，则该约束条件为xi≠xj；

输出格式

输出到文件 prog.out 中。

输出文件包括t行。

输出文件的第 k行输出一个字符串“ YES” 或者“ NO”（不包含引号，字母全部大写），“ YES” 表示输入中的第k个问题判定为可以被满足，“ NO” 表示不可被满足。

输入输出样例

输入 #1复制

2
2
1 2 1
1 2 0
2
1 2 1
2 1 1

输出 #1复制

NO
YES

输入 #2复制

2
3
1 2 1
2 3 1
3 1 1
4
1 2 1
2 3 1
3 4 1
1 4 0

输出 #2复制

YES
NO

说明/提示

【样例解释1】

在第一个问题中，约束条件为：x1=x2,x1≠x2。这两个约束条件互相矛盾，因此不可被同时满足。

在第二个问题中，约束条件为：x1=x2,x1=x2。这两个约束条件是等价的，可以被同时满足。

【样例说明2】

在第一个问题中，约束条件有三个：x1=x2,x2=x3,x3=x1。只需赋值使得x1=x1=x1，即可同时满足所有的约束条件。

在第二个问题中，约束条件有四个：x1=x2,x2=x3,x3=x4,x4≠x1。由前三个约束条件可以推出x1=x2=x3=x4，然而最后一个约束条件却要求x1≠x4，因此不可被满足。

【数据范围】

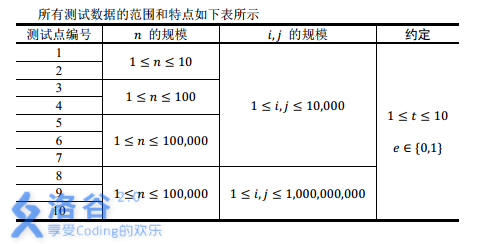
注：实际上 n\le 10^6n≤106

【时限2s，内存512M】

思路：　　　　这道题普通并查集路径压缩就行了，我们看数据范围有点大，所以再加上去重+离散化，注意是多组数据，所以数组要清零，并查集数组要清零，在for循环时，注意调用的是那个变量，弄清楚，注意函数的使用，可以先处理e==1时的，再处理e==0时的，方便判断。。

代码：

#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<algorithm>
#include<cstring>
#define N 5000000
using namespace std;
int t,n,fa[N],b[N],tot;
bool vis;
struct node
{
	int x,y,e;
}a[N];
bool cmp(const node &a,const node &b){return a.e > b.e;}
int find(int x){ return x==fa[x] ? fa[x]: fa[x]=find(fa[x]);}
int main()
{
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d",&n);
		vis=1;tot=0;
		memset(fa,0,sizeof(fa));
		memset(b,0,sizeof(b));
		memset(a,0,sizeof(a));
		for(int i=1;i<=n;i++)
		{
			scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].e);
			b[++tot]=a[i].x;
			b[++tot]=a[i].y;
		}
		sort(b+1,b+tot+1);
		int len=unique(b+1,b+tot)-b;
		for(int i=1;i<=n;i++)
		{
			a[i].x=lower_bound(b+1,b+len,a[i].x) - b;
			a[i].y=lower_bound(b+1,b+len,a[i].y) - b;
		}
		for(int i=1;i<=len;i++)fa[i]=i;
		sort(a+1,a+n+1,cmp);
		for(int i=1;i<=n;i++)
		{
			int x1=find(a[i].x);
			int y1=find(a[i].y);
			if(a[i].e)
			{
				fa[x1]=y1;
			}
			else
			{
				if(x1==y1)
				{
				vis=0;
				break;
				}
			}
		}
		if(!vis)printf("NO\n");
		else printf("YES\n");
	}
	return 0;
}

　　感谢 ----离殇