ACO 蚁群算法（算法流程，TSP例子解析）

算法 计算机 超级计算 高性能 科学探索

1. 算法背景——蚁群的自组织行为特征

高度结构化的组织——虽然蚂蚁的个体行为极其简单，但由个体组成的蚁群却构成高度结构化的社会组织，蚂蚁社会的成员有分工，有相互的通信和信息传递。

自然优化——蚁群在觅食过程中，在没有任何提示下总能找到从蚁巢到食物源之间的最短路径；当经过的路线上出现障碍物时，还能迅速找到新的最优路径。

信息正反馈——蚂蚁在寻找食物时，在其经过的路径上释放信息素（外激素）。蚂蚁基本没有视觉，但能在小范围内察觉同类散发的信息素的轨迹，由此来决定何去何从，并倾向于朝着信息素强度高的方向移动。

自催化行为——某条路径上走过的蚂蚁越多，留下的信息素也越多（随时间蒸发一部分），后来蚂蚁选择该路径的概率也越高。

 

2. 算法基本思想：

（1）根据具体问题设置多只蚂蚁，分头并行搜索。

（2）每只蚂蚁完成一次周游后，在行进的路上释放信息素，信息素量与解的质量成正比。

（3）蚂蚁路径的选择根据信息素强度大小（初始信息素量设为相等），同时考虑两点之间的距离，采用随机的局部搜索策略。这使得距离较短的边，其上的信息素量较大，后来的蚂蚁选择该边的概率也较大。

（4）每只蚂蚁只能走合法路线（经过每个城市1次且仅1次），为此设置禁忌表来控制。

（5）所有蚂蚁都搜索完一次就是迭代一次，每迭代一次就对所有的边做一次信息素更新，原来的蚂蚁死掉，新的蚂蚁进行新一轮搜索。

（6）更新信息素包括原有信息素的蒸发和经过的路径上信息素的增加。

（7）达到预定的迭代步数，或出现停滞现象（所有蚂蚁都选择同样的路径，解不再变化），则算法结束，以当前最优解作为问题的最优解。

 

3. 信息素及转移概率的计算：

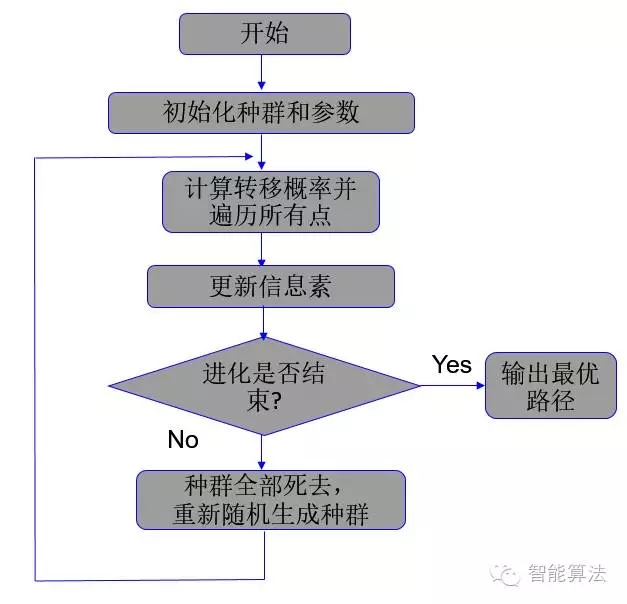
4. 算法步骤

算法流程图如下：

5. 举例分析

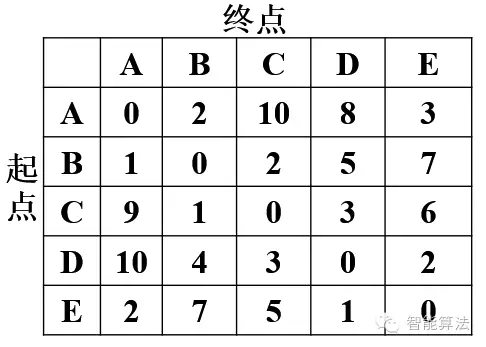
我们假设5个城市的TSP问题，然由于某种原因，城市道路均是单行道，即A->B和B->A的距离不相同，也就是说这是一个不对称的TSP问题。现在城市距离信息如下表：

设置参数：

m=5,α=1,β=1,ρ=0.5,τ_ij(0)=2。

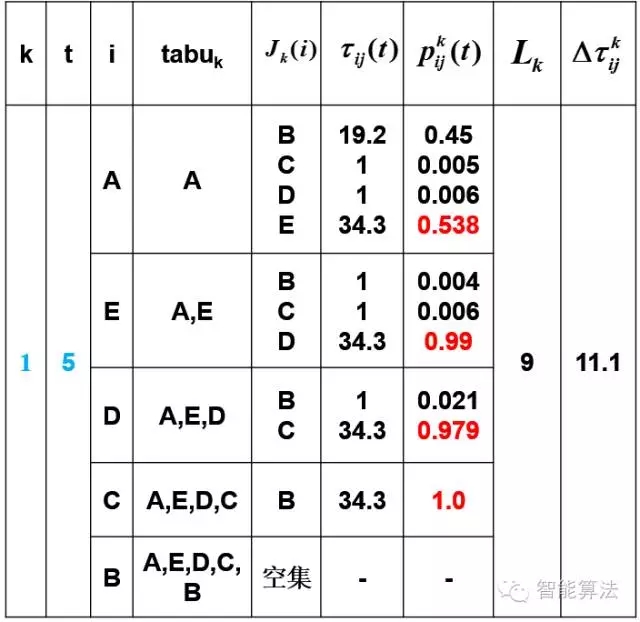
第一次迭代第一只蚂蚁：

第一次迭代第二只蚂蚁

第一次迭代第三只蚂蚁：

第一次迭代第四只蚂蚁：

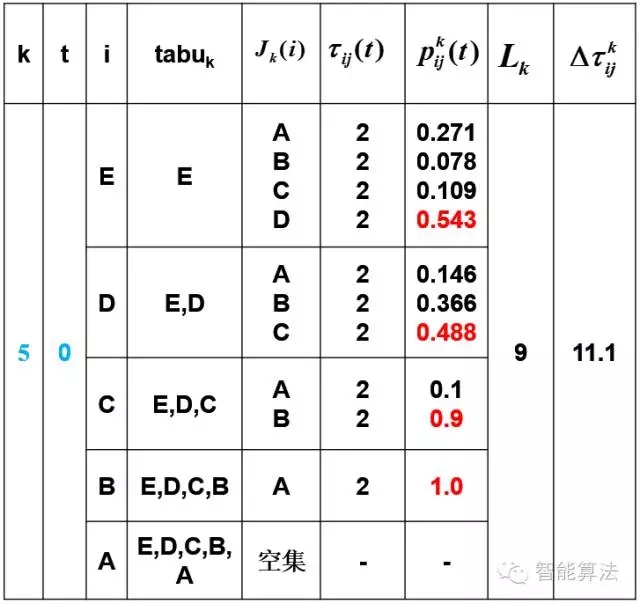
第一次迭代第五只蚂蚁：

第一次迭代完成，更新信息素矩阵，信息素挥发系数为0.5。

第一代蚂蚁全部累死，重新随机生成第二代蚂蚁进行迭代。

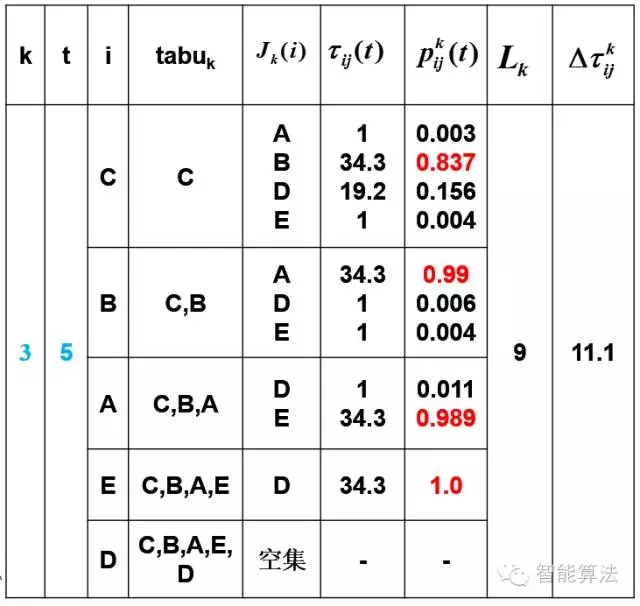
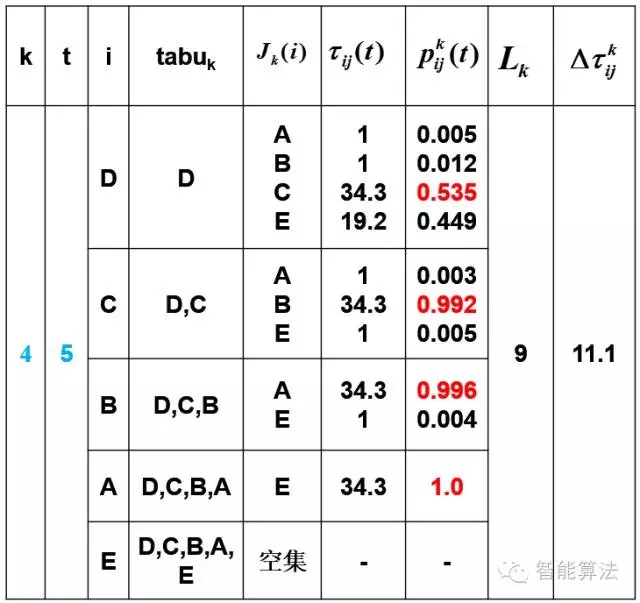
第二次迭代第一只蚂蚁：

第二次迭代第二只蚂蚁：

第二次迭代第三只蚂蚁：

第二次迭代第四只蚂蚁：

第二次迭代第五只蚂蚁：

至此，我们已经发现在第二次迭代的时候，五只蚂蚁走的是同一条路，所以算法收敛结束。    最优路径A->E->D->C->B->A, 最有路径的距离为9.

 

6. 算法特点：

是一种基于多主体的智能算法，不是单个蚂蚁行动，而是多个蚂蚁同时搜索，具有分布式的协同优化机制。

本质上属于随机搜索算法（概率算法），具有概率搜索的特征。

是一种全局搜索算法，能够有效地避免局部最优。

%--------------------------------------------------------------------------
%% 数据准备
% 清空环境变量
clear all
clc

% 程序运行计时开始
t0 = clock;
%导入数据
citys=xlsread('Chap9_citys_data.xlsx', 'B2:C53');
%--------------------------------------------------------------------------
%% 计算城市间相互距离
n = size(citys,);
D = zeros(n,n);
for i = :n
    for j = :n
        if i ~= j
            D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^));
        else
            D(i,j) = 1e-;      %设定的对角矩阵修正值
        end
    end
end
%--------------------------------------------------------------------------
%% 初始化参数
m = ;                              % 蚂蚁数量
alpha = ;                           % 信息素重要程度因子
beta = ;                            % 启发函数重要程度因子
vol = 0.2;                           % 信息素挥发(volatilization)因子
Q = ;                               % 常系数
Heu_F = ./D;                        % 启发函数(heuristic function)
Tau = ones(n,n);                     % 信息素矩阵
Table = zeros(m,n);                  % 路径记录表
iter = ;                            % 迭代次数初值
iter_max = ;                      % 最大迭代次数
Route_best = zeros(iter_max,n);      % 各代最佳路径
Length_best = zeros(iter_max,);     % 各代最佳路径的长度
Length_ave = zeros(iter_max,);      % 各代路径的平均长度
Limit_iter = ;                      % 程序收敛时迭代次数
%-------------------------------------------------------------------------
%% 迭代寻找最佳路径
while iter <= iter_max
    % 随机产生各个蚂蚁的起点城市
      start = zeros(m,);
      for i = :m
          temp = randperm(n);
          start(i) = temp();
      end
      Table(:,) = start;
      % 构建解空间
      citys_index = :n;
      % 逐个蚂蚁路径选择
      for i = :m
          % 逐个城市路径选择
         for j = :n
             has_visited = Table(i,:(j - ));           % 已访问的城市集合(禁忌表)
             allow_index = ~ismember(citys_index,has_visited);    % 参加说明1（程序底部）
             allow = citys_index(allow_index);  % 待访问的城市集合
             P = allow;
             % 计算城市间转移概率
             for k = :length(allow)
                 P(k) = Tau(has_visited(end),allow(k))^alpha * Heu_F(has_visited(end),allow(k))^beta;
             end
             P = P/sum(P);
             % 轮盘赌法选择下一个访问城市
            Pc = cumsum(P);     %参加说明2(程序底部)
            target_index = find(Pc >= rand);
            target = allow(target_index());
            Table(i,j) = target;
         end
      end
      % 计算各个蚂蚁的路径距离
      Length = zeros(m,);
      for i = :m
          Route = Table(i,:);
          for j = :(n - )
              Length(i) = Length(i) + D(Route(j),Route(j + ));
          end
          Length(i) = Length(i) + D(Route(n),Route());
      end
      % 计算最短路径距离及平均距离
      if iter ==
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min_Length;
          Length_ave(iter) = mean(Length);
          Route_best(iter,:) = Table(min_index,:);
          Limit_iter = ; 

      else
          [min_Length,min_index] = min(Length);
          Length_best(iter) = min(Length_best(iter - ),min_Length);
          Length_ave(iter) = mean(Length);
          if Length_best(iter) == min_Length
              Route_best(iter,:) = Table(min_index,:);
              Limit_iter = iter;
          else
              Route_best(iter,:) = Route_best((iter-),:);
          end
      end
      % 更新信息素
      Delta_Tau = zeros(n,n);
      % 逐个蚂蚁计算
      for i = :m
          % 逐个城市计算
          for j = :(n - )
              Delta_Tau(Table(i,j),Table(i,j+)) = Delta_Tau(Table(i,j),Table(i,j+)) + Q/Length(i);
          end
          Delta_Tau(Table(i,n),Table(i,)) = Delta_Tau(Table(i,n),Table(i,)) + Q/Length(i);
      end
      Tau = (-vol) * Tau + Delta_Tau;
    % 迭代次数加1，清空路径记录表
    iter = iter + ;
    Table = zeros(m,n);
end
%--------------------------------------------------------------------------
%% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
Time_Cost=etime(clock,t0);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route()])]);
disp(['收敛迭代次数:' num2str(Limit_iter)]);
disp(['程序执行时间:' num2str(Time_Cost) '秒']);
%--------------------------------------------------------------------------
%% 绘图
figure()
plot([citys(Shortest_Route,);citys(Shortest_Route(),)],...  %三点省略符为Matlab续行符
     [citys(Shortest_Route,);citys(Shortest_Route(),)],'o-');
grid on
for i = :size(citys,)
    text(citys(i,),citys(i,),['   ' num2str(i)]);
end
text(citys(Shortest_Route(),),citys(Shortest_Route(),),'       起点');
text(citys(Shortest_Route(end),),citys(Shortest_Route(end),),'       终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['ACA最优化路径(最短距离:' num2str(Shortest_Length) ')'])
figure()
plot(:iter_max,Length_best,'b')
legend('最短距离')
xlabel('迭代次数')
ylabel('距离')
title('算法收敛轨迹')
%--------------------------------------------------------------------------
%% 程序解释或说明
% . ismember函数判断一个变量中的元素是否在另一个变量中出现，返回0-1矩阵；
% . cumsum函数用于求变量中累加元素的和，如A=[, , , , ], 那么cumsum(A)=[, , , , ]。