c++智能指针和二叉树(1): 图解层序遍历和逐层打印二叉树

二叉树是极为常见的数据结构，关于如何遍历其中元素的文章更是数不胜数。

然而大多数文章都是讲解的前序/中序/后序遍历，有关逐层打印元素的文章并不多，已有文章的讲解也较为晦涩读起来不得要领。本文将用形象的图片加上清晰的代码帮助你理解层序遍历的实现，同时我们使用现代c++提供的智能指针来简化树形数据结构的资源管理。

那么现在让我们进入正题。

使用智能指针构建二叉树

我们这里所要实现的是一个简单地模拟了二叉搜索树的二叉树，提供符合二叉搜索树的要求的插入功能个中序遍历。同时我们使用shared_ptr来管理资源。

现在我们只实现insert和ldr两个方法，其余方法的实现并不是本文所关心的内容，不过我们会在后续的文章中逐个介绍：

struct BinaryTreeNode: public std::enable_shared_from_this<BinaryTreeNode> {
    explicit BinaryTreeNode(const int value = 0)
    : value_{value}, left{std::shared_ptr<BinaryTreeNode>{}}, right{std::shared_ptr<BinaryTreeNode>{}}
    {}

    void insert(const int value)
    {
        if (value < value_) {
            if (left) {
                left->insert(value);
            } else {
                left = std::make_shared<BinaryTreeNode>(value);
            }
        }

        if (value > value_) {
            if (right) {
                right->insert(value);
            } else {
                right = std::make_shared<BinaryTreeNode>(value);
            }
        }
    }

    // 中序遍历
    void ldr()
    {
        if (left) {
            left->ldr();
        }

        std::cout << value_ << "\n";

        if (right) {
            right->ldr();
        }
    }

    // 分层打印
    void layer_print();

    int value_;
    // 左右子节点
    std::shared_ptr<BinaryTreeNode> left;
    std::shared_ptr<BinaryTreeNode> right;

private:
    // 层序遍历
    std::vector<std::shared_ptr<BinaryTreeNode>> layer_contents();
};

我们的node对象继承自enable_shared_from_this，通常这不是必须的，但是为了在层序遍历时方便操作，我们需要从this构造智能指针，因此这步是必须的。insert会将比root小的元素插入左子树，比root大的插入到右子树；ldr则是最为常规的中序遍历，这里实现它是为了以常规方式查看tree中的所有元素。

值得注意的是，对于node节点我们最好使用make_shared进行创建，而不是将其初始化为全局/局部对象，否则在层序遍历时会因为shared_ptr的析构进而导致对象被销毁，从而引发未定义行为。

现在假设我们有一组数据：[3, 1, 0, 2, 5, 4, 6, 7]，将第一个元素作为root，将所有数据插入我们的树中会得到如下的一棵二叉树：

auto root = std::make_shared<BinaryTreeNode>(3);
root->insert(1);
root->insert(0);
root->insert(2);
root->insert(5);
root->insert(4);
root->insert(6);
root->insert(7);

可以看到节点一共分成了四层，现在我们需要逐层打印，该怎么做呢？

层序遍历

其实思路很简单，我们采用广度优先的思路，先将节点的孩子都打印，然后再去打印子节点的孩子。

以上图为例，我们先打印根节点的值3，然后我们再打印它的所有子节点的值，是1和5，然后是左右子节点的子节点，以此类推。。。。。。

说起来很简单，但是代码写起来却会遇到麻烦。我们不能简单得像中序遍历时那样使用递归来解决问题（事实上可以用改进的递归算法），因为它会直接来到叶子节点处，这不是我们想要的结果。不过不要紧，我们可以借助于队列，把子节点队列添加到队列末尾，然后从队列开头也就是根节点处遍历，将其子节点添加进队列，随后再对第二个节点做同样的操作，遇到一行结束的地方，我们使用nullptr做标记。

先看具体的代码：

std::vector<std::shared_ptr<BinaryTreeNode>>
BinaryTreeNode::layer_contents()
{
    std::vector<std::shared_ptr<BinaryTreeNode>> nodes;
    // 先添加根节点，根节点自己就会占用一行输出，所以添加了作为行分隔符的nullptr
    // 因为需要保存this，所以这是我们需要继承enable_shared_from_this是理由
    // 同样是因为这里，当返回的结果容器析构时this的智能指针也会析构
    // 如果我们使用了局部变量则this的引用计数从1减至0，导致对象被销毁，而使用了make_shared创建的对象引用计数是从2到1，没有问题
    nodes.push_back(shared_from_this());
    nodes.push_back(nullptr); // 为根元素所在层添加分隔符
    // 我们使用index而不是迭代器，是因为添加元素时很可能发生迭代器失效，处理这一问题将会耗费大量精力，而index则无此烦恼
    for (int index = 0; index < nodes.size(); ++index) {
        if (!nodes[index]) {
            // 当前层节点的子节点都已经添加进了队列此时遍历到了分隔符或已经遍历到队列末尾
            if (index == nodes.size()-1) {
                break; // 这时我们到达了队尾，遍历结束
            }

            nodes.push_back(nullptr); // 为当前层的下一层添加分隔符，第一层的节点已经事先添加
            continue;
        }

        if (nodes[index]->left) { // 将当前节点的子节点都添加进队列
            nodes.push_back(nodes[index]->left);
        }
        if (nodes[index]->right) {
            nodes.push_back(nodes[index]->right);
        }
    }

    return nodes;
}

代码本身并不复杂，重要的是其背后的思想。

算法图解

如果你第一遍并没有读懂这段代码也不要紧，下面我们有请图解上线：

首先是循环开始时的状态，第一行的内容已经确定了(^代表空指针)：

然后我们从首元素开始遍历，第一个遍历到的是root，他有两个孩子，值分别是1和5：

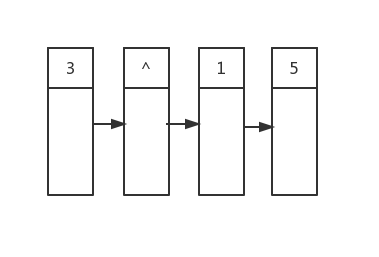
接着索引值+1，这次遍历到的是nullptr，因为不是在队列末尾，所以我们简单添加一个nullptr在队列末尾，这样第二行的节点就都在队列中了：

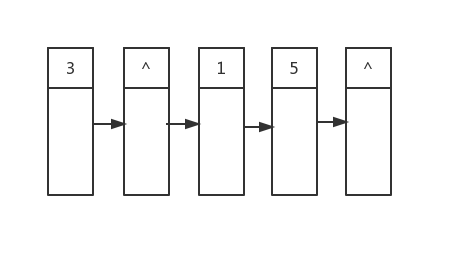
随后我们开始遍历第二行的节点，将它们的子节点作为第三行的内容放入队列，最后加上一个行分隔符，以此类推：

简单来说，就是通过队列来缓存上一行的所有节点，然后再根据上一行的缓存得到下一行的所有节点，循环往复直到二叉树的最后一层。当然不只是二叉树，其他多叉树的层序遍历也可以用类似的思想实现。

好了，知道了如何获取每一行的内容，我们就能逐行处理节点了：

void BinaryTreeNode::layer_print()
{
    auto nodes = layer_contents();
    for (auto iter = nodes.begin(); iter != nodes.end(); ++iter) {
        // 空指针代表一行结束，这里我们遇到空指针就输出换行符
        if (*iter) {
            std::cout << (*iter)->value_ << " ";
        } else {
            std::cout << "\n";
        }
    }
}

如你所见，这个方法足够简单，我们把节点信息保存在额外的容器中是为了方便做进一步的处理，如果只是打印的话大可不必这么麻烦，不过简单通常是有代价的。对于我们的实现来说，分隔符的存在简化了我们对层级之间的区分，然而这样会导致浪费至少log2(n)+1个vector的存储空间，某些情况下可能引起性能问题，而且通过合理得使用计数变量可以避免这些额外的空间浪费。当然具体的实现读者可以自己挑战一下，原理和我们上面介绍的是类似的因此就不在赘述了，也可以参考园内其他的博客文章。

测试

最后让我们看看完整的测试程序，记住要用make_shared创建root实例：

int main()
{
    auto root = std::make_shared<BinaryTreeNode>(3);
    root->insert(1);
    root->insert(0);
    root->insert(2);
    root->insert(5);
    root->insert(4);
    root->insert(6);
    root->insert(7);
    root->ldr();
    std::cout << "\n";
    root->layer_print();
}

输出：

可以看到上半部分是中序遍历的结果，下半部分是层序遍历的输出，而且是逐行打印的，不过我们没有做缩进。所以不太美观。

另外你可能已经发现了，我们没有写任何有关资源释放的代码，没错，这就是智能指针的威力，只要注意资源的创建，剩下的事都可以放心得交给智能指针处理，我们可以把更多的精力集中在算法和功能的实现上。

另一种层序遍历

上一节提到的方法中我们只是把节点分层后储存在容器中等待进一步处理，这样实现的好处是简单，然而代价是性能，不仅要存储额外的分层标志，还需要多次遍历容器。

我们当然可以避免这些弊端，只要稍微让代码复杂一点点：

void layer_print2()
{
    std::queue<NodeType> q;
    q.push(shared_from_this());

    while (!q.empty()) {
        auto layer_len = q.size(); // 获取当前待处理层中节点的个数

        while (layer_len--) { // 逐个处理当前层内的元素
            auto node = q.front();
            std::cout << node->value_ << " ";

            if (node->left) {
                q.push(node->left);
            }

            if (node->right) {
                q.push(node->right);
            }
            q.pop();
        }

        // 遍历完了一层
        std::cout << std::endl;
    }
}

代码很简单，不过我还是要解释一下。

这里我们借助了队列，先将每一层的节点都存入队列，然后我们再获得队列的长度，这个长度就是当前待处理层中的节点数。随后我们遍历这些节点，把它们的孩子再存入队列，形成了下一层待处理的节点。当内层循环结束时就说明当前层已经处理完，这时可以针对该层进行额外的处理，比如我们在这里输出一个换行符。

换句话说，在这个方案中我们记录了每层拥有的节点数以此来确定是否遍历完了一层，而不是额外存储一个代表当前层次结束的标记符。

智能指针和层序遍历的内容到这里就结束了，在下一篇文章中我们还将看到智能指针和二叉树的更多操作。

如有错误和疑问欢迎指出！