N元模型

在自然语言处理的任务中，拼音纠错、机器翻译等任务都需要对某个句子的下一个单词进行预测，或者评估某个句子的概率大小。例如预测如下句子的下一个单词：

Please turn your home work...

在这个语境中，我们可能会预测下一个单词是over或是in，而不是预测为the或其他单词。

像这种对自然语言的句子进行建模，并赋予单词或句子概率的模型称为语言模型(LMs,Language Models)。在这篇博客中将介绍一种最简单的语言模型-n元模型。n元模型对N个单词组成的序列进行建模，例如2-元模型、3-元模型等。2-元模型就是两个单词组成的序列，比如please turn,turn your,your homework等等。

N元模型

根据语境预测下一个单词是什么的任务可以形式化的表示为：已知history h，求下一个单词是w的概率 $P(w|h) $。例如

\[ P(the|\ its\ water\ is\ so\ transparent\ that\ ) \]

如果有一个很大的语料库（比如web语料），我们可以采用频率估计的方法计算上式，这个问题可以转化为

\[ P(w|h) = \frac {P(hw)}{P(h)} = \frac {Count(hw)}{Count(h)} \]

\[ P(the|\ its\ water\ is\ so\ transparent\ that\ ) =\frac {P(\ its\ water\ is\ so\ transparent\ that\ the\ )}{P(\ its\ water\ is\ so\ transparent\ that\ )} = \frac {Count(\ its\ water\ is\ so\ transparent\ that\ the\ )}{Count(\ its\ water\ is\ so\ transparent\ that\ )}\]

即分别计算在语料库中its water is so transparent that the出现的次数和its water is so transparent that出现的次数，然后做除法。这种方法在一些任务上的效果很好，但在一些任务中不能给出很好的结果，主要原因有以下两点：

语言具有创造性：新的句子和单词的组合方式总是在出现，我们不能总是计算整个句子的概率。而且在这种方法中，即使只是简单的对例句进行了扩展也可能会产生句子的出现概率为0的情况。
计算量过大：在这种计算方式下，如果我们想要计算its water is so transparent出现的概率，我们首先需要获得语料库中这个句子出现的次数，还要计算语料库中所有五个单词组成的句子的次数。毫无疑问，这种方法的计算量太大了。
我们需要采用一种更好的方法来计算，首先可以采用链式法则将整个句子的概率计算简化为如下形式

\[ P(w^{n}_{1}) = P(w_{1})P(w_{2}|w_{1})P(w_{3}|w^{2}_{1})....P(w_{n}|w^{n-1}_{1}) \]

但是\(P(w_{n}|w^{n-1}_{1})\)的概率还是无法计算。N元模型的思想是，将history简化为最近的几个单词。例如在二元模型中，\(P(w_{n}|w^{n-1}_{1}) = P(w_{n}|w_{n-1})\)。也就是在计算\(P(the|\ its\ water\ is\ so\ transparent\ that\ )\)的概率时近似的用 $P(the|that) $来代替。
这种采用 \(P(w_{n}|w_{n-1})\) 来近似 \(P(w_{n}|w^{n-1}_{1})\) 的假设称为马尔科夫假设。马尔科夫模型是指在预测的时候不过多的考虑前文的一系列模型。将马尔科夫假设应用到N元模型中为：\(P(w_{n}|w^{n-1}_{1})\ =\ P(w_{n}|w^{n-1}_{n-N+1})\)
对二元模型来说，$ P(w^{n}{1}) $的的计算可以简化为如下公式：
\[ P(w^{n}_{1})\ =\ \prod^{n}_{k=1} P(w_{k}|w_{k-1})\]
在这个公式中，模型的参数是所有的 \(P(w_{k}w_{k-1}),P(w_{k-1})\)。极大似然估计可以证明，在n次实验、m种可能结果的情况下，如果我们已知每种结果发生的频次，可以用 \(P(p_{i})=\frac{n_{i}}{n}\) 作为对第i种结果的概率估计，即用频率估计参数。在本模型中，m种可能的结果为$ w{k}$的各种排列组合结果，n为语料库的语句，则可得到如下式子：
\[ P(w_{n}|w_{n-1})=\frac{C(w_{n-1}w_{n})}{\sum_{w}{C(w_{n-1}w)}} \]
其中 \(\sum_{w}{C(w_{n-1}w)}\) 计算了\(w_{n-1}\)的各种后缀的数目总和。其实就是\(w_{n-1}\)的总数。则上式可以简化为
\[ P(w_{n}|w_{n-1})=\frac{C(w_{n-1}w_{n})}{C(w_{n-1})} \]将整个式子推广到一般情况可得
\[ P(w_{n}|w^{n-1}_{n-N+1})=\frac{C(w^{n-1}_{n-N+1}w_{n})}{C(w^{n-1}_{n-N+1})} \]

将二元模型应用在实际中我们可以看到统计学可以将语法知识，甚至文化等编码进概率。比如eat的后面常常跟着一个名字或者副词，to后面常常跟着一个动词等语法常识，或者是I通常是一句话的开头等个人习惯，以及人们寻求中餐的概率比英式食物的概率要高等文化习俗。另外，由于概率是介于0和1之间的浮点数，在将多个概率相乘后得到的数可能会非常小，因此我们常常对概率取log进行表示。

语言模型的评估

评估一个语言模型的最好方法是将它放在应用系统中，看这个模型为系统带来了多少提升。这种方法被称为外部测试（extrinsic evaluation）。外部测试可以准确的知道这个模型对系统是否真的有用，但是这种测试的代价太高，一版不会使用。相对的，我们一般采用内部测试，内部测试的思想是独立于任何一个应用系统对模型进行测试。
内部测试需要测试集（test set）和训练集（training set）。我们拿到一份语料后，将其划分为训练集和测试集两部分。模型在训练集上进行参数训练，在测试集上评估模型效果。需要注意的是，测试集和训练集的数据不能有交叉，测试集必须是模型“没有见过”的数据。那么在测试集上如何评估模型效果呢？如果模型能更准确地预测数据或是更紧的收敛于测试集，就称这个模型的效果更好。
有时我们频繁的使用某个测试集，会使得模型隐式地被这个测试集校准。这时我们需要一个全新的测试集来评估模型，之前的测试集又被称为开发集（development set）。那我们如何将我们的数据集划分为训练集、开发集和测试集呢？我们不仅希望测试集足够大（小的测试集可能不具有代表性），又希望获得更多的训练数据。我们可以选择在能够提供足够的统计数据测试模型的效果的前提下的最小测试集。在实践中，我们通常将数据集划分为80%的训练集，10%开发集和10%的测试集。
困惑度
我们一般不直接使用模型的测试结果作为模型的评价指标，而是一种叫做困惑度（perplexity，pp）的变量。模型的困惑度是模型在测试集上的概率被词汇数N规范化以后的值。例如，测试集\(W=w_{1}w_{2}w_{3}...w_{N}\)的困惑度为
\[ PP(W)= P(w_{1}w_{2}w_{3}...w_{N})^{-\frac{1}{N}} = \sqrt[N]{\frac{1}{P(w_{1}w_{2}w_{3}...w_{N})}}\]
我们可以采用链式法则进行简化
\[ PP(W)= \sqrt[N]{\prod^{N}_{i=1}{\frac{1}{P(w_{i}|w_{1}...w_{i-1})}}} \]
应用二元模型可得
\[ PP(W)=\sqrt[N]{\prod^{N}_{i=1}{\frac{1}{P(w_{i}|w_{i-1})}}} \]
可以看到，要最大化模型在测试集上的概率，可以通过最小化困惑度来完成。

接下来我们通过一个例子来看困惑度如何比较模型的效果。基于华尔街日报训练的三个模型：一元模型、二元模型和三元模型的困惑度如下表所示：

\	一元模型	二元模型	三元模型
困惑度	962	170	109

可以看出，模型提供的信息量越大（三元模型），模型的困惑度就越低，单词的后继词汇就越确定。需要注意的是，在比较困惑度时，必须基于同一个测试集。

采用模型生成语句

像很多统计模型一样，N元模型也依赖于训练语料。这意味着模型中编码了训练集中的一些特定信息，而且随着N的增大，N元模型对训练集的建模效果会越来越好。下面我们将直观的反应N元模型的这两个特点。
我们采用香农和米勒在1951年提出的生成随机语句的方法来展示N元模型的特点。一元模型是最容易展示的。
一元模型生成语句算法：

• 为词汇赋予概率：根据每个词汇的频率为其赋予一个0到1之间的数字
• 产生随机数序列：产生一个随机数序列，每个随机数都在0到1之间

• 根据随机数序列产生随机语句：随机序列中的每个随机数a都可以找到一个词汇，该词汇的概率为a

  根据上述算法可以产生一元模型的随机语句。类似的，我们可以得到二元模型的随机语句，其产生算法如下所示：

• 计算每个二元词组的概率P(a|b)
• 假设句子的开始标志为<s>，从所有以<s<开始的二元组中随机选出一组，假设这组为(<s>,w)

• 接下来从以w开头的二元组中随机选择一组，重复这两个过程，直到产生结束符</s>

下面给出四个模型产生的随机语句：

模型	随机语句
一元模型	-To him swallowed confess hear both.Which .Of save on trail for are ay device and rote life have . -Hill he late speaks;or! a more to leg less first you enter
二元模型	-Why dost stand forth thy canopy,forsooth;he is this palpable hit the King Henry.Live king.Follow. -What means,sir.I confess she?then all sorts,he is trim,captain.
三元模型	-Fly,and will rid me these news of price.Therefore the sadness of parting,as they say,'tis done. -This shall forbid it should be branded ,if renown made it empty.
四元模型	-King Henry.What! I will go seek the traitor Gloucester.Exeunt some of the watch. A great banquet serv'd in; -It cannot be but so.

这八条语句由四个N元模型产生，训练语料均为莎士比亚的作品。可以看出，模型训练的上下文越长，句子越连贯。在一元模型中，单词之间没有关联，二元模型中单词之间有一些关联，三元模型和四元模型生成的语句看起来就很像莎士比亚的风格了。It cannot be but so直接来自《King John》。
为了理解模型对训练语料的依赖，我们在另外一个语料（华尔街日报）上重新训练了这四个模型。结果如下：

模型	随机语句
一元模型	Months the my and issue of year foreign new exchange's september were recession exchange new endorsed a acquire to six executives.
二元模型	Last December through the way to preserve the Hudson corporation N.B.E.C.Taylor would seem to complete the major central planners one point five percent of U.S.E. has already old M.X. corporation of living on information such as more frequently fishing to keep her
三元模型	They also point to ninety nine point six billion dollars from two hundred four oh six three percent of the rates of interest stores as Mexico and Brazil on market conditions.

比较在两个语料上生成的模型可以发现，两个模型生成的语句之间没有交叉，甚至是词组上也没有交叉。可见，如果训练集是莎士比亚作品而测试集是华尔街日报，那么这个模型将会变得无用。因此，在训练N元模型时，我们需要确认训练集和测试集是同一种类型的语料。同时，语料的语气等也需要加以区分，尤其是与正式文稿或口语化文稿相关的任务。
语料的类型和语气等匹配了仍然不够，我们的模型还受到语料稀疏度的影响。由于语料的有限性，一些很常见的语句可能不被包含在内，造成一些“零概率短语”实际上应该拥有非零值的概率。比如在华尔街日报的语料中，denied the有以下短语：

• denied the allegations:5
• denied the speculation:2
• denied the rumors:1
• denied the report:1
  如果训练集中包含下述语料他们的概率将会被视为0：
• denied the offer
• denied the load

除了二元概率为0的情况（没见过的词汇组合），我们还可能会在测试集中遇到完全没见过的单词。这种情况下应该怎么办呢？
有时我们的语言模型不可能会遇到没出现过的词汇。这种封闭词汇袋（closed vocabulary）的假设在某些语言任务中是合理的假设，例如语音识别、机器翻译等，这些任务中我们会提前设置好发音词典，语言模型只需要识别词典中出现过的词汇。
在其他的任务中，我们必须处理之前没有遇到过的词汇（unknown words，或者成为oov，out of vocabulary）。OOV出现的比例被称为OOV率。开放词汇袋（Open vocabulary）系统是指我们通过一个伪词汇<UNK>来对测试集中可能出现的unknown word进行建模的系统。下面介绍两种训练带有<UNK>词汇训练集的方法。
第一种方法将这个问题转化为封闭词袋问题。首先选择一个固定的词汇集，然后在文本正则化（text normalization）的过程中，将不属于固定词汇集的单词替换为<UNK>。根据频率估计<UNK>的概率。
第二种方法主要针对无法事先准备一个词袋的情况，这时我们可以构建一个词典，将训练集中的一些单词替换为<UNK>。比如我们可以将出现的频率低于n的单词都替换为<UNK>，其中n是一个很小的数字。或者设定一个词袋的容量N，对词袋中所有的词汇频率进行统计并排序，取前N个词汇组成固定词袋，剩下的词汇是unknown word。

平滑（smoothing）

接下来解决一种新的情景：某个在训练集中出现过的单词，在测试集里出现在一种新的语境中，该如何计算？为了使语言模型在这种情况下不会赋予短语0概率，我们需要将高频事件的概率匀一部分给未知的新事件。这种概率的修改称为平滑（smoothing）或者折扣（discount），下面将介绍几种平滑方式：add-1 smoothing,add-k smoothing,stupid backoff和Kneser-Ney smoothing。

Laplace Smoothing

最简单的平滑方式是在计算概率之前，为所有的二元词组的计数都加一。之前频数为1的词组变成2，频数为2的词组变成3。这平滑方式又被称为拉普拉斯平滑（Laplace Smoothing）。拉普拉斯平滑虽然在现在的很多模型中表现不是很好，但是可以为我们引入许多平滑的术语，并为其他的平滑方式提供一个基准线（baseline），而且在文本分类等任务中有较好的效果。
我们可以先尝试将拉普拉斯平滑加入一元模型中。根据极大似然估计计算一元模型中某个词的概率公式为：
\[ P(w_{i})=\frac{c_{i}}{N} \]
其中\(w_{i}\)为训练集中的词汇，\(c_{i}\)为\(w_{i}\)的频数，\(N\)为所有词汇的频数总和。拉普拉斯平滑只是为每个词汇的频数都加1。假设训练集中共有\(V\)个词汇，因此公式中的分母相应的调整为\(N+V\)。完整的公式如下：
\[P(w_{i})=\frac{c_{i}+1}{N+V}\]
我们可以定义一个新的变量\(c^{*}_{i}\)作为系数，在计算一个词汇的平滑概率时不用同时改变分子、分母，只需要将原来的概率乘以该系数即可。\(c^{*}_{i}\)的定义如下：
\[c^{*}_{i}=(c_{i}+1)*\frac{N}{N+V}\]
现在我们可以将\(c^{*}_{i}\)直接除以\(N\)得到概率\(P^{*}_{i}\)。我们可以通过另一种方式描述这种平滑：词汇的原始频数与平滑后的频数之比，也即词汇频数的折扣\(discount \ d_{c}\):
\[d_{c}=\frac{c^{*}}{c}\]
现在我们有了一元模型的平滑计算方法，继续看二元模型的拉普拉斯平滑。二元模型的概率计算方法为：
\[P(w_{n}|w_{n-1})=\frac{C(w_{n-1}w_{n})}{C(w_{n-1})}\]
二元模型的平滑即为给每个二元词组的共现频数都加一。计算公式改为如下形式：
\[P^{*}_{Laplace}(w_{n}|w_{n-1})=\frac{C(w_{n-1}w_{n})+1}{\sum_{w}{(C(w_{n-1}w)+1)}}=\frac{C(w_{n-1}w_{n})+1}{C(w_{n-1})+V}\]
通过上面的公式我们计算出二元概率模型中每个二元词组的概率。二元模型的平滑系数计算方法如下：
\[c^{*}(w_{n-1}w_{n})=P^{*}_{Laplace}*C(w_{n-1})=\frac{[C(w_{n-1}w_{n}+1)]*C(w_{n-1})}{C(w_{n-1})+V}\]
以下两个表格分别是二元模型在某一语料上的平滑前和平滑后的频数。

\	i	want	to	eat	chinese	food	lunch	spend
i	5	827	0	9	0	0	0	2
want	2	0	608	1	6	6	5	1
to	2	0	4	686	2	0	6	211
eat	0	0	2	0	16	2	42	0
chinese	1	0	0	0	0	82	1	0
food	15	0	15	0	1	4	0	0
lunch	2	0	0	0	0	1	0	0
speed	1	0	1	0	0	0	0	0

以下是平滑后的频数表：

\	i	want	to	eat	chinese	food	lunch	spend
i	3.8	527	0.64	6.4	0.64	0.64	0.64	1.9
want	1.2	0.39	238	0.78	2.7	2.7	2.3	0.78
to	1.9	0.63	3.1	430	1.9	0.63	4.4	133
eat	0.34	0.34	1	0.34	5.8	1	15	0.34
chinese	0.2	0.098	0.098	0.098	0.098	8.2	0.2	0.098
food	6.9	0.43	6.9	0.43	0.86	2.2	0.43	0.43
lunch	0.57	0.19	0.19	0.19	0.19	0.38	0.19	0.19
speed	0.32	0.16	0.32	0.16	0.16	0.16	0.16	0.16

从上面两个表可以看出拉普拉斯平滑对词汇的频数改变是很大的。\(C(want to)\)的频数从608降到了238！计算频数的折扣可以看出频数的变化是多么剧烈，\(C(chinese food)\)的折扣率竟然高达10！这种频数和概率的剧烈变化是因为我们从高频词的地方借来了太多概率！

add-k smoothing

既然add-1平滑的折扣率太高了，一个很自然的想法是降低从高频词汇那里匀出来的概率，每个词的频数不是加1，而是加上一个小于1的浮点数k，这种方法被称为add-k smoothing。
\[P^{*}_{Add-k}(w_{n}|w_{n-1}) = \frac{C(w_{n-1}w_{n})+k}{C(w_{n-1})+kV}\]
add-k 平滑要求我们有选择k的算法，例如我们可以通过在dev集上优化k值。尽管add-k smoothing在一些任务上很有效（包括文本分类的任务），但它应用在语言模型上的效果仍然不是很好，平滑后的频数要么对原频数没什么改变，要么有着不恰当的折扣率。

backoff and interpolation

add-1平滑和add-k平滑可以解决N元模型的词汇零频数问题，但是N元模型的零值问题还包含另一种情况：假设我们要计算\(P(w_{n}|w_{n-2}w_{n-1})\)，但是我们没有\(w_{n-2}w_{n-1}w_{n}\)的词组，我们可以退而求其次，计算二元概率\(P(w_{n}|w_{n-1})\)代替三元概率。类似的，如果我们没有二元概率\(P(w_{n}|w_{n-1})\)，可以使用一元概率\(P(w_{n})\)进行代替。
换句话说，有时在训练的时候少一点上下文可以模型的泛化能力。有两种方法利用这种n元模型之间的“继承关系”，分别是后退和插值。当模型无法估计N元词组时，后退一步选用N-1元模型替代，这种方法称为后退。而插值的方法会利用所有的N元模型信息。

插值算法

当估计一个三元词组的概率时，加权结合三元模型、二元模型和一元模型的结果。线性插值是相对简单的插值方法，将N个模型的结果做线性组合。利用线性插值估计三元词组的概率时，公式如下：
\[P(w_{n}|w_{n-1}w_{n-2})=\lambda_{1}P(w_{n}|w_{n-1}w_{n-2})+\lambda_{2}P(w_{n}|w_{n-1})+\lambda_{3}P(w_{n}) \]
其中所有的\(\lambda\)和为1，\(\sum_{i}\lambda_{i}=1\)
稍微复杂一点的情况是，根据上下文来计算\(\lambda\)的值，计算公式如下：
\[P(w_{n}|w_{n-1}w_{n-2})=\lambda_{1}(w^{n-1}_{n-2})P(w_{n}|w_{n-1}w_{n-2})+\lambda_{2}(w^{n-1}_{n-2})P(w_{n}|w_{n-1})+\lambda_{3}(w^{n-1}_{n-2})P(w_{n}) \]
公式中的\(\lambda\)值如何确定呢？线性插值和条件插值中的\(\lambda\)值都可以通过held-out corpus学习得到的，其中held-out语料是一个附加训练集，用于训练超参数（比如上面的\(\lambda\)）。比如，固定N元模型的概率，寻找使\(P(w_{n}|w_{n-1}w_{n-2})\)最大的\(\lambda\)值，可以采用EM算法确定\(\lambda\)值。

后退算法

在使用后退算法计算概率时，如果N元词组计算的概率为0，使用N-1元近似来N元词组的概率。为了维持概率分布的正确性，在后退算法中，需要对higher-order概率折扣处理。如果higher-order的概率不进行折扣处理，而是直接使用lower-order的概率去近似，概率空间会被扩大，概率和将大于1。比如\(P(w_{n}|w_{n-1})\)的概率明显比\(P(w_{n})\)概率小，如果直接用一元概率替代，所有二元概率的概率和将大于一。因此，我们需要用一个函数\(\alpha\)来均衡概率分布。
这种有折扣的后退方法被称为Katz backoff。在Katz后退方法中，如果\(C(w^{n}_{n-N+1})\)不为0，那么概率值为折扣概率\(P^{*}\)，如果\(C(w^{n}_{n-N+1})\)是0，就递归地退回N-1的短上下文情境中计算概率并乘以\(\alpha\)函数的结果，具体公式如下所示：

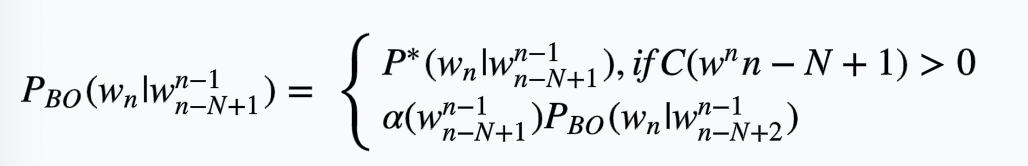
Katz后退通常跟Good-Turing平滑方法结合在一起使用。

Kneser-Ney算法

Kneser-Ney将绝对折扣算法加以扩充，能更好的处理地lower-order模型的概率分布。现在考虑这样一个问题，采用二元模型和一元模型预测一句话中的下一个单词，举例如下：
I can't see without my reading...
单词glasses是比较合理的后继词汇，因此我们希望一元模型能预测出glasses而不是Kong。但是由于Hong Kong是一个很常见的词组，一元模型给Kong赋予的概率要比glasses高。对比Kong和glasses两个词汇可以发现，虽然Kong是一个很常见的词汇，但是Kong一般只出现在Hong之后，而glasses的分布更为广泛。也就是说，在一个新的语境中，一元模型预测的概率不应该只是：这个词汇出现的概率有多大？而是：这个词汇在新语境中出现的概率有多大？我们将这种新的概率记为\(P_{CONTINUATION}\)。KN算法通过统计词汇w出现在不同语境中的次数来计算\(P_{CONTINUATION}\)，其假设为一个单词在过去出现在不同语境中的频率越高，在未来出现在新语境中的可能性就越高。即为
\[P_{CONTINUATION}(w) \propto | {v:C(vw)>0}|\]
为了将这种正比关系转化为概率公式，我们可以用所有二元词组的数目来正则化。即：
\[P_{CONTINUATION}(w)=\frac{| {v:C(vw)>0}|}{|{(u',w'):C(u'w')>0|}}\]
另一种归一化的方法是采用单词w的所有前继的后继数目之和，公式如下：
\[P_{CONTINUATION}(w)=\frac{| {v:C(vw)>0}|}{\sum_{w'}|{(vw')>0|}}\]
在这个公式中高频词汇Kong的概率很低，达到了我们的预期。最终的KN插值公式如下：
\[P_{KN}(w_{i}|w_{i-1})=\frac{max(C(w_{i-1}w_{i})-d,0)}{C(w_{i-1})}+\lambda(w_{i-1})P_{CONTINUATION}(w_{i})\]
其中\(\lambda\)的计算方法为：
\[\lambda(w_{i-1})=\frac{d}{\sum_{v}{C(w_{i-1}w)}}|\{w:C(w_{i-1}w)>0|\}\]
其中第一项\(\frac{d}{\sum_{v}{C(w_{i-1}w)}}\)计算了\(w_{i-1}\)的所有后继的频数之和，第二项\(|\{w:C(w_{i-1}w)>0|\}\)计算了\(w_{i-1}\)的后继种类。
将KN公式推广到一般情况，递归公式如下：
\[P_{KN}(w_{i}|w^{i-1}_{i-n+1})=\frac{max(c_{KN}(w^{i}_{i-n+1})-d,0)}{\sum_{v}{c_{KN}(w^{i-1}_{i-n+1}v)}}+\lambda(w^{i-1}_{i-n+1})P_{KN}(w_{i}|w^{i-1}_{i-n+2})\]
其中\(count()\)函数的值取决于计算的是highest-order的频数还是lower-ouder的频数。如果是highest-order，则直接计算频数即可，如果是lower-ouder则计算其语境的数目。即：

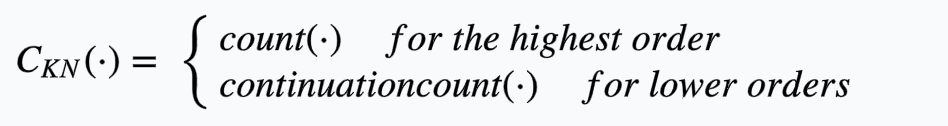
递归过程的最后一步是均匀分布\(\frac{1}{V}\)的一元插值，参数\(\epsilon\)是一个空字符串，计算公式如下：
\[P_{KN}(w)=\frac{max(c_{KN}(w)-d,0)}{\sum_{w'}{c_{KN}(w')}}+\lambda(\epsilon)\frac{1}{V}\]
KN插值算法的效果最好的版本是modified Kneser-Ney smoothing，该算法不只使用一个\(d\)进行计算折扣，而是用了三个折扣参数\(d_{1},d_{2},d_{3}\)，分别用于频数为1、2和3及以上频数的词汇。

网络和后退算法

web极大的丰富了自然语言处理的语料库，有了网络，训练high-oder的N元模型成为可能。google在2016年发布了一个极大的N元词组count集，包括从一元到五元所有词组的频数。要在大规模语料集上构建语言模型，性能问题需要慎重考虑。例如字符串形式的单词放在磁盘上，内存中只放一个64位的哈希码。还有其他的方式来缩减N元模型的大小：仅仅存储频数大于某个阈值的N元词组或是利用熵去掉某些不重要的N元词组。
尽管有了这些方法的帮助，我们可以在web语料集上采用KN平滑算法，但是Brants在2007年的研究结果表明没有必要采用KN等复杂算法，当语料集合非常大时（例如web语料），简单的平滑算法反而更加有效。这种简单的算法就是后退算法（stupid backoff）。后退算法不会平衡概率分布，当higher-order的概率为0时，直接后退到lower-order进行代替，计算公式如下：

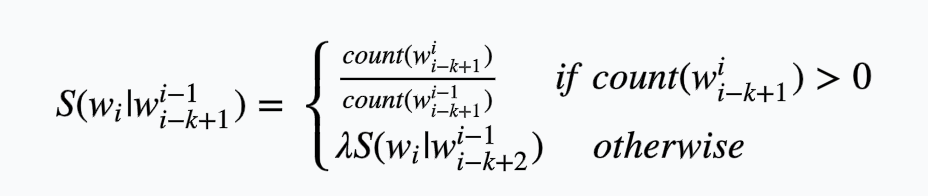
后退算法在一元模型时停止，此时概率\(S(w)=\frac{count(w)}{N}\)，此外Brants在2007年给出了\(\lambda\)的优值0.4。