[Search Engine] 搜索引擎技术之倒排索引

　　倒排索引是搜索引擎中最为核心的一项技术之一，可以说是搜索引擎的基石。可以说正是有了倒排索引技术，搜索引擎才能有效率的进行数据库查找、删除等操作。

1. 倒排索引的思想

　　倒排索引源于实际应用中需要根据属性的值来查找记录。这种索引表中的每一项都包括一个属性值和具有该属性值的各记录的地址。由于不是由记录来确定属性值，而是由属性值来确定记录的位置，因而称为倒排索引(inverted index)。

　　在搜索引擎中，查询词可以切分成若干个单词，所以对于搜索引擎中的倒排索引对应的属性就是单词，而对应的记录就是网页（也可以广泛地称为是文档）。所以，搜索引擎中的倒排索引是实现“单词-文档矩阵”的一种具体存储形式，通过倒排索引，可以根据单词（属性）快速获取包含这个单词的文档列表（记录）。倒排索引主要由两个部分组成：“单词词典”和“倒排文件”。

2. “单词-文档矩阵”

　　单词-文档矩阵是表达两者之间所具有的一种包含关系的概念模型，图1展示了其含义。图1的每列代表一个文档，每行代表一个单词，打对勾的位置代表包含关系：

图1 单词-文档矩阵

从纵向即文档这个维度来看，每列代表文档包含了哪些单词，比如文档1包含了词汇1和词汇4，而不包含其它单词。从横向即单词这个维度来看，每行代表了哪些文档包含了某个单词。比如对于词汇1来说，文档1和文档4中出现过单词1，而其它文档不包含词汇1。矩阵中其它的行列也可作此种解读。

搜索引擎的索引其实就是实现“单词-文档矩阵”的具体数据结构。可以有不同的方式来实现上述概念模型，比如“倒排索引”、“签名文件”、“后缀树”等方式。但是各项实验数据表明，“倒排索引”是实现单词到文档映射关系的最佳实现方式。

3. 倒排索引的基本框架

　　单词和单词字典：搜索引擎的通常索引单位是单词，单词词典是由文档集合中出现过的所有单词构成的字符串集合，单词词典内每条索引项记载单词本身的一些信息以及指向“倒排列表”的指针。

　　倒排列表：倒排列表记载了出现过某个单词的所有文档的文档列表及单词在该文档中出现的位置信息，每条记录称为一个倒排项(Posting)。根据倒排列表，即可获知哪些文档包含某个单词。

　　倒排文件：所有单词的倒排列表往往顺序地存储在磁盘的某个文件里，这个文件即被称之为倒排文件，倒排文件是存储倒排索引的物理文件。

　　搜索引擎中倒排索引大概流程框架：用户在搜索引擎搜索框输入查询词进行搜索时，搜索引擎会对查询词进行切词以及近义词匹配等操作，根据原始查询词得到一系列的单词列表。然后根据搜索引擎内部的字典来查询每个单词对应的倒排列表，从而定位到包含这个单词的网页或者说是文档。最后搜索引擎根据特定的网页排序算法将查询到的网页进行排序，通过前端将搜索结果展示给用户。下图2为倒排索引的主要流程：

图2 倒排索引流程框架

4. 单词字典

　　其实，我们通过上述倒排索引的流程也可以看出来，倒排索引的关键技术在于建立单词字典。

　　单词词典用来维护文档集合中出现过的所有单词的相关信息，同时用来记载某个单词对应的倒排列表在倒排文件中的位置信息。在支持搜索时，根据用户的查询词，去单词词典里查询，就能够获得相应的倒排列表，并以此作为后续排序的基础。
      对于一个规模很大的文档集合来说，可能包含几十万甚至上百万的不同单词，能否快速定位某个单词，这直接影响搜索时的响应速度，所以需要高效的数据结构来对单词词典进行构建和查找，常用的数据结构包括哈希加链表结构（哈希存储的拉链法）和树形词典结构。
　　1）哈希拉链法
　　图3是这种词典结构的示意图。这种词典结构主要由两个部分构成：

　　主体部分是哈希表，每个哈希表项保存一个指针，指针指向冲突链表，在冲突链表里，相同哈希值的单词形成链表结构。之所以会有冲突链表，是因为两个不同单词获得相同的哈希值，如果是这样，在哈希方法里被称做是一次冲突，可以将相同哈希值的单词存储在链表里，以供后续查找。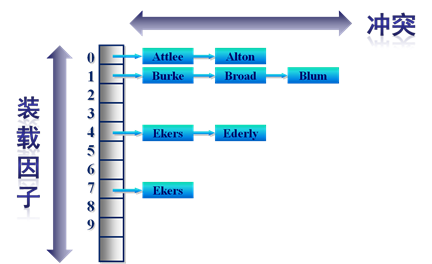

图3 哈希拉链法词典结构

在建立索引的过程中，词典结构也会相应地被构建出来。比如在解析一个新文档的时候，对于某个在文档中出现的单词T，首先利用哈希函数获得其哈希值，之后根据哈希值对应的哈希表项读取其中保存的指针，就找到了对应的冲突链表。如果冲突链表里已经存在这个单词，说明单词在之前解析的文档里已经出现过。如果在冲突链表里没有发现这个单词，说明该单词是首次碰到，则将其加入冲突链表里。通过这种方式，当文档集合内所有文档解析完毕时，相应的词典结构也就建立起来了。

在响应用户查询请求时，其过程与建立词典类似，不同点在于即使词典里没出现过某个单词，也不会添加到词典内。以图3为例，假设用户输入的查询请求为单词X，对这个单词进行哈希，定位到哈希表内的4号槽，从其保留的指针可以获得冲突链表，依次将单词X和冲突链表内的单词比较，发现单词X在冲突链表内，于是找到这个单词，之后可以读出这个单词对应的倒排列表来进行后续的工作，如果没有找到这个单词，说明文档集合内没有任何文档包含单词，则搜索结果为空。

　　2）树形结构
　　B树（或者B+树）是另外一种高效查找结构，图1-8是一个 B树结构示意图。B树与哈希方式查找不同，需要字典项能够按照大小排序（数字或者字符序），而哈希方式则无须数据满足此项要求。
　　B树形成了层级查找结构，中间节点用于指出一定顺序范围的词典项目存储在哪个子树中，起到根据词典项比较大小进行导航的作用，最底层的叶子节点存储单词的地址信息，根据这个地址就可以提取出单词字符串。

5. 倒排索引的实例

　　假设文档集合包含五个文档，每个文档内容如图4所示，在图中最左端一栏是每个文档对应的文档编号。我们的任务就是对这个文档集合建立倒排索引。

图4 文档集合

　　中文和英文等语言不同，单词之间没有明确分隔符号，所以首先要用分词系统将文档自动切分成单词序列。这样每个文档就转换为由单词序列构成的数据流，为了系统后续处理方便，需要对每个不同的单词赋予唯一的单词编号，同时记录下哪些文档包含这个单词，在如此处理结束后，我们可以得到最简单的倒排索引（参考图3-4）。在图3-4中，“单词ID”一栏记录了每个单词的单词编号，第二栏是对应的单词，第三栏即每个单词对应的倒排列表。比如单词“谷歌”，其单词编号为1，倒排列表为{1,2,3,4,5}，说明文档集合中每个文档都包含了这个单词。

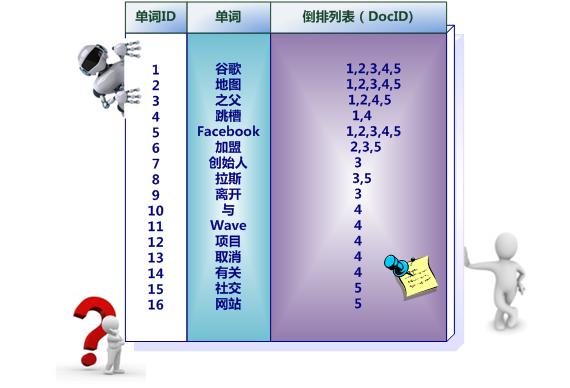
图5 简单的倒排索引

　　之所以说图5所示倒排索引是最简单的，是因为这个索引系统只记载了哪些文档包含某个单词，而事实上，索引系统还可以记录除此之外的更多信息。在单词对应的倒排列表中不仅记录了文档编号，还可以记载了单词频率信息（TF），即这个单词在某个文档中的出现次数，之所以要记录这个信息，是因为词频信息在搜索结果排序时，计算查询和文档相似度是很重要的一个计算因子，所以将其记录在倒排列表中，以方便后续排序时进行分值计算     实用的倒排索引还可以记载更多的信息，图6所示索引系统除了记录文档编号和单词频率信息外，额外记载了两类信息，即每个单词对应的“文档频率信息”（对应图6的第三栏）。

图6 带有单词频率、文档频率和出现位置信息的倒排索引

　　此外，除了上述信息，还可以在倒排列表中记录单词在某个文档出现的位置信息。

图6所示倒排索引已经是一个非常完备的索引系统，实际搜索系统的索引结构基本如此，区别无非是采取哪些具体的数据结构来实现上述逻辑结构。

有了这个索引系统，搜索引擎可以很方便地响应用户的查询，比如用户输入查询词“Facebook”，搜索系统查找倒排索引，从中可以读出包含这个单词的文档，这些文档就是提供给用户的搜索结果，而利用单词频率信息、文档频率信息即可以对这些候选搜索结果进行排序，计算文档和查询的相似性，按照相似性得分由高到低排序输出，最后为用户展示出搜索结果。