codeforces 441C. Valera and Tubes 解题报告

题目链接：http://codeforces.com/problemset/problem/441/C

题目意思：将n * m 的矩阵分成 k 堆。每堆是由一些坐标点（x, y）组成的。每堆里面至少由 >= 2 个坐标点组成，这些坐标点还需要满足： |x_i - x_i + 1| + |y_i - y_i + 1| = 1 。这个等式表示遍历堆里面的坐标好像蛇形那样走，也就是坐标点与坐标点之间需要相邻！还有一个条件就是，每个坐标点只能用一次。

做了一整天= =。改了一个问题，另一个问题又出现了。终于被一个问题攻陷了= =。

整体思路就是 k - 1堆中，每堆由两个坐标组成，剩下的那一堆，由剩下未用的坐标构成。由于我做的时候是一竖竖地做的（假设 3 * 5的矩阵，1 1 1 2 2 1 2 2...），所以有个问题就是剩下的那堆，从第一行开始走的时候，是从左到右走还是从右到左走？我错误的代码中，判断不了对于分完k-1堆之后，箭头是如何走的！我是通过k-1堆之后被覆盖的总行数的奇偶数来判断的：奇数：从左至右，偶数：从右至左。但是对于行数为奇数来说，就不行了。以下这两种情况足以证实。

5  9  20

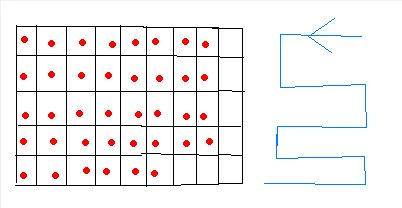 （被覆盖的总行数为奇数，但正确走法应该是从右至左）

2   2  1

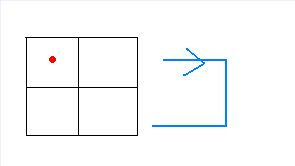  （与推测相同）

先贴下我错的代码（读者可直接忽略），一场噩梦= =

（test 24 错了，说堆中有些tube 不符合条件）

 #include <iostream>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 using namespace std;

 const int maxn =  + ;
 int vis[maxn][maxn];

 int main()
 {
     int n, m, k;
     while (scanf("%d%d%d", &n, &m, &k) != EOF)
     {
         memset(vis, , sizeof(vis));
         int row = , y = ;
         int cnt, tmp, f = , sum = ;
         for (cnt = ; cnt <= k-; )
         {
             if (y+ > m)
                 break;
             printf("2 %d %d %d %d\n", row, y, row, y+);
             vis[row][y] = vis[row][y+] = ;
             sum += ;
             row++;
             cnt++;
             if (!(row % n) && cnt+ <= k-)
             {
                 printf("2 %d %d %d %d\n", row, y, row, y+);
                 vis[row][y] = vis[row][y+] = ;
                 sum += ;
                 y += ;
                 row = ;
                 f = ;
                 cnt++;
             }
         }
         int col = m;
         for (int row = ; row+ <= n && cnt <= k-; row += , cnt++)
         {
             printf("2 %d %d %d %d\n", row, col, row+, col);
             vis[row][col] = vis[row+][col] = ;
             sum += ;
         }
         tmp = (!f ? row- : n);
       //  printf("tmp = %d\n", tmp);
         if ((n*m)-sum)
         {
             printf("%d ", n*m-sum);
             int start = (tmp& ?  : );  // 奇数顺着来走
             for (int row = ; row <= n; row++)
             {
                 if (start)
                 {
                     for (int col = ; col <= m; col++)
                     {
                         if (!vis[row][col])
                             printf("%d %d ", row, col);
                     }
                 }
                 else
                 {
                     for (int col = m; col >= ; col--)
                     {
                         if (!vis[row][col])
                             printf("%d %d ", row, col);
                     }
                 }
                 start ^= ;
             }
         }
         printf("\n");
     }
     return ;
 }

AC代码（真是简单就为美啊～～～）

规规矩矩，一行行顺着来做

 #include <iostream>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 using namespace std;

 int n, m, k;

 void next(int &x, int &y)
 {
     if (y == )
     {
         if (x & )
             y++;
         else
             x++;
     }
     else if (y == m)
     {
         if (x & )
             x++;
         else
             y--;
     }
     else if (x & )
         y++;
     else
         y--;
 }

 int main()
 {
     while (scanf("%d%d%d", &n, &m, &k) != EOF)
     {
         int x = , y = ;
         int cnt = k;
         while (cnt > )
         {
             printf("");
             printf(" %d %d", x, y);
             next(x, y);
             printf(" %d %d\n", x, y);
             next(x, y);
             cnt--;
         }
         printf("%d", n*m-*(k-));
         while (x >=  && x <= n && y >=  && y <= m)
         {
             printf(" %d %d", x, y);
             next(x, y);
         }
         puts("");
     }
     return ;
 }