「咕咕网校 - 基础省选」树上问题的进阶 by Drench

一定要在noip之前把自己花钱买的Luogu网课梳理完！QAQ

树上前缀和：

对于有根树，在每个点记录 val （点权）和 sum（到根的点权之和）

当然记录的值因题而异（但是既然叫树上前缀和当然就要这么定义啊）

就可以做一些奇奇怪怪的操作了。

还是看题来理解这玩意儿的妙用吧2333

EG1

给定树和各点点权，t次询问，每次求u到v路径上的点权和。（1e5）

是道板子题了。

从根开始dfs，到每个点时记录该点的val和sum

其中sum为该点到祖先路径上点权之和，包括自己。

每次输出sum[u]+sum[v]-2*sum[lca(u,v)]+val[lca(u,v)]。

EG2

给定初始点权为0的树，n次操作，每次对u,v路径上每点+x。

求最后每点点权。（1e5）

运用差分思想。

对每个点记录一个val值，初始为0。

对于每次操作：

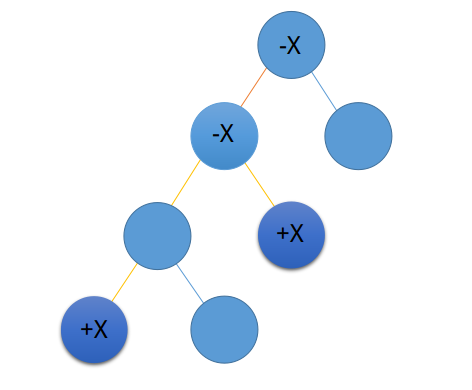
如图，两个深色的是u和v，黄色是u,v的路径。

推一推就会神奇（并不）的发现，每个点的真实点权就是该点的子树点权和。

val[u]+=x;

val[v]+=x;

val[lca(u,v)]-=x;

if(fa[lca(u,v)]!=lca[u,v])
fa[lca(u,v)]-=x;

实现O(4)修改，最后用O(n)得到答案。

“经典的树上差分。”——ddd

EG3

给定树，边有边权。

求有多少对（u,v）使u,v路上所有边的边权异或和为0（1e5）
其中异或和=所有数异或起来的结果

记sum[x]为x到祖先的异或和。

由于异或有：

a xor a =

所以如下图，在sum[u] xor sum[v]时，lca以上的屎色线已经被消掉了。

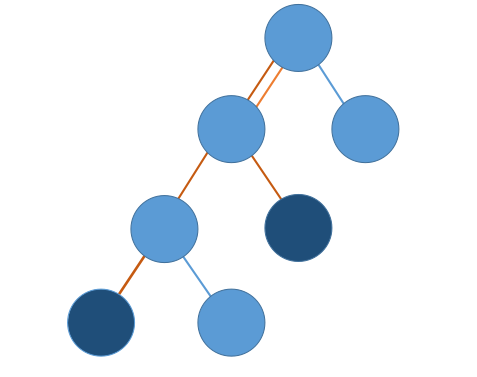
所以ans=sum[u] xor sum[v]

问题转化为：有1e5个数（sum），求中间有多少对数异或和=0

也就是有多少对相等的数。

用一个map记录，然后遍历map就行了。

EG4（留坑

给定一棵N个节点的树，每个点有一个权值val（1e9），对于第M（1e5）个询问(u,v,k)，回答u和v这两个节点间第K小的点权。

权值线段树+前缀和。

前置知识：

权值线段树：以val为下标的树。
EG:

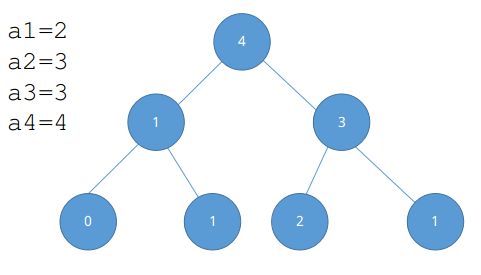
对于序列版本（在序列上问l到r之间第k大的数）：

每加入一个新的点，只会对权值线段树上的logn个点产生影响。

所以从左往右每加入一个新点，就可持久化一下。

对于每个询问，算出[1,l-1]的权值线段树和[l,r]的权值线段树，减一下就星了。

（以下照抄ppt）

“对于树上版本，每个点从其父亲的版本可持久化而来。

那么对于一条路径，和树上前缀和一样，由4棵线段树即可提取出这条路径表示的权值线段树。

再在线段树上查询即可。”

好像还要四个主席树怎么搞一搞吧2333

我连可持久化都不会你跟我说这些东西？！！

DFS序

此物如名，就是dfs的顺序。

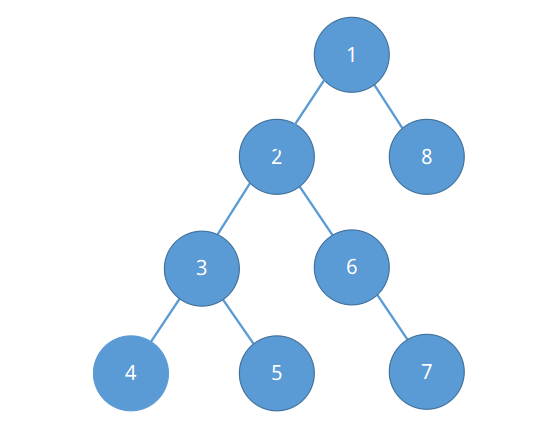
如图，如果按照前序遍历（根->左->右）去搜的话，搜索序就会是这样。

搜索的方法可以根左右可以根右左，记录也有只在进入时记一次和进入弹出都记啊什么的，大同小异。

对于我们现在讨论的这种dfs序，有这样一个神奇的性质：

一个树的子树中的点，在dfs序上是连续的。
换言之，设该点为i，它在dfs序上的位置为pos，子树大小为siz。
则它的子树中的点在[pos,pos+siz-1]上。

这玩意儿我们可以联系代码解释：

 void dfsx(int x)

 {

     cout<<x<<" ";

     for(int i=heap[x];i;i=a[i].next)

     {

         dfsx(a[i].to);

     }

     return;

 }

差不多是这样，想一想就能通了（吧）

EG

给定一棵有n个节点的树。

有两种操作：

.给u的子树上每点+v

.求u的子树上的点权和（1e5）

是道板子题了。

根据我们之前搞出来的dfs序，可以把对子树的操作转化为区间问题（区间加区间求和）

然后线段树就行了。

以及dfs序还在LCA的ST法上有用，多年前的ST学习笔记。

树链剖分（轻重链剖分）

对于一个点，我们记它的所有儿子中，子树最大的一个儿子为重儿子，连接该儿子的边为重边（深色边）；否则为轻边。

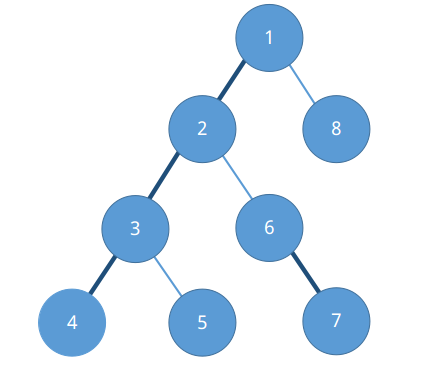
如图。

性质：从根到某一点的路径上，有不超过logn条轻边，不超过logn条重边。

代码实现方面：（口胡ing 等我口胡完就代码实现

首先扫一遍，得到哪些点是重儿子->哪些边是重边

然后对每个点，记fa[x]为x的父节点，top[x]为x在只走重链的前提下的祖先

恭喜你得到了一棵剖好了的树！

LCA（1e5）

对于u,v：
若top[u]==top[v]，则lca为u,v中深度较小的那个点；
否则把链头较深的点 跳到链头的父亲处。

本质上还是算暴力跳的鬼畜优化吧（挠头

LA（一个点向上x步的祖先）（1e5）

对于查询u向上x步：

设当前点dep[u]，目标祖先的dep就是dep[u]-x；

如果top[u]的dep比目标dep深，那么跳到链头的父亲处；（logn）

否则：

目标点肯定在当前点到top的路上。

也就是在这条重链上，所以在dfs序上连续。

从而所求点的dfn就是 top的dfn 加上 它到top的dep差。O()

EG6

树剖模板。

我解决掉啦！

EG7

给定树，有点权。

操作：1.从u到v路径上每点点权+t

2.求所有于u点相邻的点的点权和

记每个点的轻儿子之和为sum[x]。

对于每次修改，暴力做轻儿子（树剖嘛）

每次查询该点的sum和重儿子和fa。

换根意义下的操作

————to be continued