NOI2015 软件包管理器(树链剖分+线段树)

P2146 软件包管理器

题目描述

Linux用户和OSX用户一定对软件包管理器不会陌生。通过软件包管理器，你可以通过一行命令安装某一个软件包，然后软件包管理器会帮助你从软件源下载软件包，同时自动解决所有的依赖（即下载安装这个软件包的安装所依赖的其它软件包），完成所有的配置。ebian/Ubuntu使用的apt-get，Fedora/CentOS使用的yum，以及OSX下可用的homebrew都是优秀的软件包管理器。

你决定设计你自己的软件包管理器。不可避免地，你要解决软件包之间的依赖问题。如果软件包A依赖软件包B，那么安装软件包A以前，必须先安装软件包B。同时，如果想要卸载软件包B，则必须卸载软件包A。现在你已经获得了所有的软件包之间的依赖关系。而且，由于你之前的工作，除0号软件包以外，在你的管理器当中的软件包都会依赖一个且仅一个软件包，而0号软件包不依赖任何一个软件包。依赖关系不存在环（若有m(m≥2)个软件包A1,A2,A3,⋯,Am，其中A1依赖A2，A2依赖A3，A3依赖A4，……，A[m-1]依赖Am，而Am依赖A1，则称这m个软件包的依赖关系构成环），当然也不会有一个软件包依赖自己。

现在你要为你的软件包管理器写一个依赖解决程序。根据反馈，用户希望在安装和卸载某个软件包时，快速地知道这个操作实际上会改变多少个软件包的安装状态（即安装操作会安装多少个未安装的软件包，或卸载操作会卸载多少个已安装的软件包），你的任务就是实现这个部分。注意，安装一个已安装的软件包，或卸载一个未安装的软件包，都不会改变任何软件包的安装状态，即在此情况下，改变安装状态的软件包数为0。

输入输出格式

输入格式：

从文件manager.in中读入数据。

输入文件的第1行包含1个整数n，表示软件包的总数。软件包从0开始编号。

随后一行包含n−1个整数，相邻整数之间用单个空格隔开，分别表示1,2,3,⋯,n−2,n−1号软件包依赖的软件包的编号。

接下来一行包含1个整数q，表示询问的总数。之后q行，每行1个询问。询问分为两种：

install x：表示安装软件包x

uninstall x：表示卸载软件包x

你需要维护每个软件包的安装状态，一开始所有的软件包都处于未安装状态。

对于每个操作，你需要输出这步操作会改变多少个软件包的安装状态，随后应用这个操作（即改变你维护的安装状态）。

输出格式：

输出到文件manager.out中。

输出文件包括q行。

输出文件的第i行输出1个整数，为第i步操作中改变安装状态的软件包数。

输入输出样例

输入样例#1：

7
0 0 0 1 1 5
5
install 5
install 6
uninstall 1
install 4
uninstall 0

输出样例#1：

3
1
3
2
3

输入样例#2：

10
0 1 2 1 3 0 0 3 2
10
install 0
install 3
uninstall 2
install 7
install 5
install 9
uninstall 9
install 4
install 1
install 9

输出样例#2：

1
3
2
1
3
1
1
1
0
1

说明

【样例说明 1】

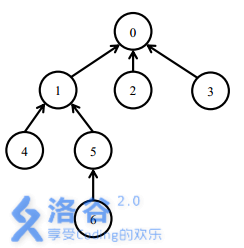
一开始所有的软件包都处于未安装状态。

安装5号软件包，需要安装0,1,5三个软件包。

之后安装6号软件包，只需要安装6号软件包。此时安装了0,1,5,6四个软件包。

卸载1号软件包需要卸载1,5,6三个软件包。此时只有0号软件包还处于安装状态。

之后安装4号软件包，需要安装1,4两个软件包。此时0,1,4处在安装状态。最后，卸载0号软件包会卸载所有的软件包。`

【数据范围】

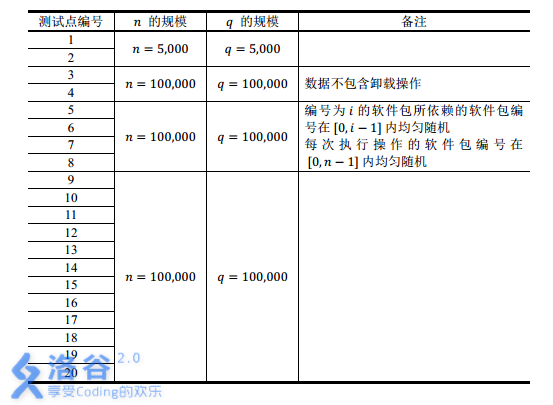
【时限1s，内存512M】

/*
每次安装软件，就把根节点到x软件路径上的值全部变为1
同理，每次卸载软件，就把x以及它的子树的值变为0
修改子树的时候用dfs序变成序列 线段树
*/
#include<iostream>
#include<cstdio>
#include<cstring>

#define N 100001

using namespace std;
int n,m,ans,cnt,tot,num;
int fa[N],head[N],deep[N],siz[N],top[N];
int S[N],T[N];
struct tree
{
    int l,r,sum,len,flag;
}tr[N<<];
struct edge
{
    int u,v,net;
}e[N<<];

inline int read()
{
    int x=,f=;char c=getchar();
    while(c>''||c<''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}

inline void add(int u,int v)
{
    e[++cnt].v=v;e[cnt].net=head[u];head[u]=cnt;
}

inline void pushup(int k)
{
    tr[k].sum=tr[k<<].sum+tr[k<<|].sum;
}

inline void pushdown(int k)
{
    if(tr[k].len==) return;
    if(tr[k].flag==)
    {
        tr[k<<].sum=tr[k<<|].sum=;
        tr[k<<].flag=tr[k<<|].flag=;
    }
    else
    {
        tr[k<<].sum=tr[k<<].len;
        tr[k<<|].sum=tr[k<<|].len;
        tr[k<<].flag=tr[k<<|].flag=;
    }
    tr[k].flag=;
}

void build(int k,int l,int r)
{
    tr[k].l=l;tr[k].r=r;
    tr[k].len=r-l+;
    if(l==r) return;
    int mid=l+r>>;
    build(k<<,l,mid);build(k<<|,mid+,r);
}

int query(int k,int l,int r)
{
    if(tr[k].l==l && tr[k].r==r) return tr[k].sum;
    if(tr[k].flag) pushdown(k);
    pushup(k);
    int mid=tr[k].l+tr[k].r>>;
    if(r<=mid) return query(k<<,l,r);
    else if(l>mid) return query(k<<|,l,r);
    else return query(k<<,l,mid)+query(k<<|,mid+,r);
}

void change(int k,int l,int r,int otk)
{
    if(tr[k].l==l && tr[k].r==r)
    {
        tr[k].flag=otk;
        if(otk==) tr[k].sum=;
        else tr[k].sum=tr[k].len;
        return;
    }
    if(tr[k].flag) pushdown(k);
    int mid=tr[k].l+tr[k].r>>;
    if(r<=mid) change(k<<,l,r,otk);
    else if(l>mid) change(k<<|,l,r,otk);
    else change(k<<,l,mid,otk),change(k<<|,mid+,r,otk);
    pushup(k);
}

void dfs1(int u)
{
    siz[u]=;
    for(int i=head[u];i;i=e[i].net)
    {
        int v=e[i].v;
        if(fa[u]==v) continue;
        deep[v]=deep[u]+;
        fa[v]=u;dfs1(v);
        siz[u]+=siz[v];
    }return;
}

void dfs2(int u,int Top)
{
    int k=-;S[u]=++tot;top[u]=Top;
    for(int i=head[u];i;i=e[i].net)
    {
        int v=e[i].v;
        if(fa[u]==v) continue;
        if(siz[v]>siz[k]) k=v;
    }if(k!=-) dfs2(k,Top);
    for(int i=head[u];i;i=e[i].net)
    {
        int v=e[i].v;
        if(fa[u]==v || v==k) continue;
        dfs2(v,v);
    }T[u]=tot;
}

int solve(int x)
{
    ans=;
    while(top[x]!=)
    {
        ans+=(S[x]-S[top[x]]+)-query(,S[top[x]],S[x]);
        change(,S[top[x]],S[x],);
        x=fa[top[x]];
    }
    ans+=(S[x]-S[top[x]]+)-query(,S[top[x]],S[x]);
    change(,S[top[x]],S[x],);
    return ans;
}

int main()
{
    n=read();int x;
    for(int i=;i<n;i++)
    {
        x=read();
        add(i,x);add(x,i);
    }
    dfs1(),dfs2(,);
    build(,,tot);
    m=read();char ch[];
    for(int i=;i<=m;i++)
    {
        scanf("%s",&ch);x=read();
        if(ch[]=='i') printf("%d\n",solve(x));
        else
        {
            printf("%d\n",query(,S[x],T[x]));
            change(,S[x],T[x],);
        }
    }
    return ;
}