JS 从斐波那契数列浅谈递归

一、前言

昨晚下班后，经理出于兴趣给我们技术组讲了讲算法相关的东西，全程一脸懵逼的听，中途还给我们出了一道比较有趣的爬楼问题，问题如下：

假设一个人从地面开始爬楼梯，规定一步只能爬一坎或者两坎，人只能往上走，例如爬到第一坎，很明显从地面到第一坎只有一种可选方式，从地面爬到第二坎，他可以从地面直接跨到第二坎，也可以先从地面到第一坎，再从第一坎到第二坎，也就是2种可选方式，那么求他爬到N楼一共有几种可选方式。

这道题涉及到了斐波那契数列，要求使用递归来求值，技术贼菜的我也是一脸懵逼，所以本着学习的心还是记录下来了。

二、有趣的斐波那契数列

我们将地面理解为数字0，第一坎理解为数字1，以此来进行简单的分析：

例如从0到1，就一种选择，如图(公司不让用破解软件，没PS画图，凑合看吧，画图的手微微颤抖。。。)

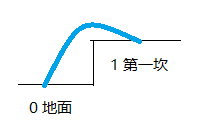
那么，现在要求到第二坎，从0到2呢，两种选择，看图分析(记住，一步只能跨一坎或者两坎)：

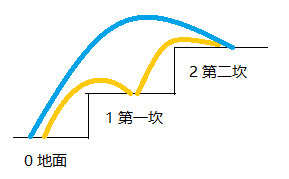
当要求从0到3，三种选择，如图：

紫色：一坎坎的走；黄色：先走两坎，再走一坎；蓝色：先走一坎，再走两坎。

从0-4，一共五种情况，如图：

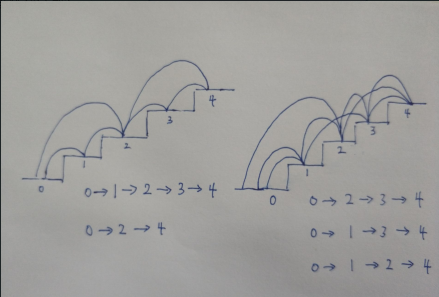
这里我分开画了，左边的2种情况加上右边的三种情况

左边：

第一种：一坎坎的走，0-1-2-3-4

第二种：两坎两坎走，0-2-4

右边：

第三种：先走两坎，再一坎坎的走0-2-3-4

第四种：先走一坎，再走两坎，再走一坎0-1-3-4

第五种：先走一坎，再走一坎，再走两坎0-1-2-4

当我们继续往后画，楼梯层对应走法会形成一个有趣的规律，

从第三层开始，第三层的走法等于一层与二层走法的和，第四层的走法等于第二层和第三层走法的和.....针对楼梯问题，我们可以得到如下公式：

F(n) = F(n-1) + F(n-2)   n>=3

这就是著名的斐波那契数列（Fibonacci sequence），又称黄金分割数列。有兴趣的同学可以查查兔子繁殖问题。

百科里斐波那契数列的基数n>=4是根据实际情况来定的，这点不用纠结。

三、斐波那契数列与递归的结合

什么是递归？自己调用自己的函数就是递归，这么说完全没问题。

我们回归上面的问题，要求第N层的走法，那我们只需要知道N-1层和N-2层的走法就好了，假设N是10，求到第十层的走法。

十层走法=九层的走法+八层走法

九层和八层也可以拆分啊，九层走法 = 七层走法 + 八层走法 ，而八层走法 = 七层走法 + 六层走法

.......

当分到3层时，最后还可以拆分为1层+2层，因为规律是从第三层开始的，因为此公式不适用于1层和2层，分到1层和2层就代表分支的结束了。

使用闭包需要找到跳出自己调用自己的的临界条件，不然会会陷入死循环，那对应我们的楼梯问题，只要N<3时就不需要继续调用自己了，因为不需要继续产生分支了。

这个闭包怎么写呢？我们结合斐波那契数列公式尝试一下吧。

现在有一个函数，里面申明一个走法变量var step = 0；输入一个数字N，我们会对N判断，只要N>=3，它就会自己调用自己，小于3时，我们分别判断它等于1或者2，等于1就让step加1，等于2就让step加2，如下：

function recursion(n){
    let step = ;
    if (n ===  ){
        step +=
    }else if (n === ){
        step += ;
    }else if (n >= ){
        step = recursion(n-) + recursion(n-);
    };
    return step;
};
console.log(recursion())//89种

为了验证，我将上方分支图中所有的1与2相加(1层只有1种走法，2层有2种)，得出数字也确实是89。所以我不明白我为什么要把基数N设置为10，算的难受。

那么趁热打铁，活学活用，现在我们尝试求正整数N与N之前所有正整数累加的和。

例如3之前累加的和就是3+2+1,数字0加不加没意义，所以跳出递归的临界条件就是当N>=2时，最后调用一次让之前数字的和加一次1就好了。

var result = ;
function add(n){
    result += n
    n>= ? add(n-) : null;
    return result;
};
console.log(add());//

验证一下，完全没问题，有没有觉得递归挺简单。

当你看到这时，恭喜你，不仅了解了斐波那契数列，也简单了解了递归的用法。其实本人在工作中需要操作数据，本能的总是想到穷举，循环，那么现在又多了一种可行的解决方法，也算是对于思维的开拓了。

留个问题，回到上方两段实现代码，为什么第一个变量申明在函数体内，而第二个数字累加的变量申明要在函数体外呢？尝试思考下。

当然，前提是，这篇博客如果有人愿意看完就挺好了。