2018-2019-20172329 《Java软件结构与数据结构》第六周学习总结
2018-2019-20172329 《Java软件结构与数据结构》第六周学习总结
学无止境,希望自己可以坚持下去,就算自己有太多的事情也不希望自己落下学习,也希望自己可以活成自己想要的样子!!加油吧!❤️
教材学习内容总结
《Java软件结构与数据结构》第十章-树
一、概述
1、什么是树:树是一种非线性结构,其中的元素被组织成一个层次结构。
2、树的组成部分:树由一个包含结点和边的集构成,其中的元素被存储在这些结点中,边则将一个结点和另个结点连接起来。每一结点都位于该树层次中的某些特定层上。树的根就是那个位于该树顶层的唯一结点。(注:一棵树只有一个根结点。)
3、位于树中叫底层的结点是上一层结点的孩子。
4、一个结点只有一个双亲,但是一个结点可以有多个孩子。
5、同一双亲的两个结点称为兄弟。
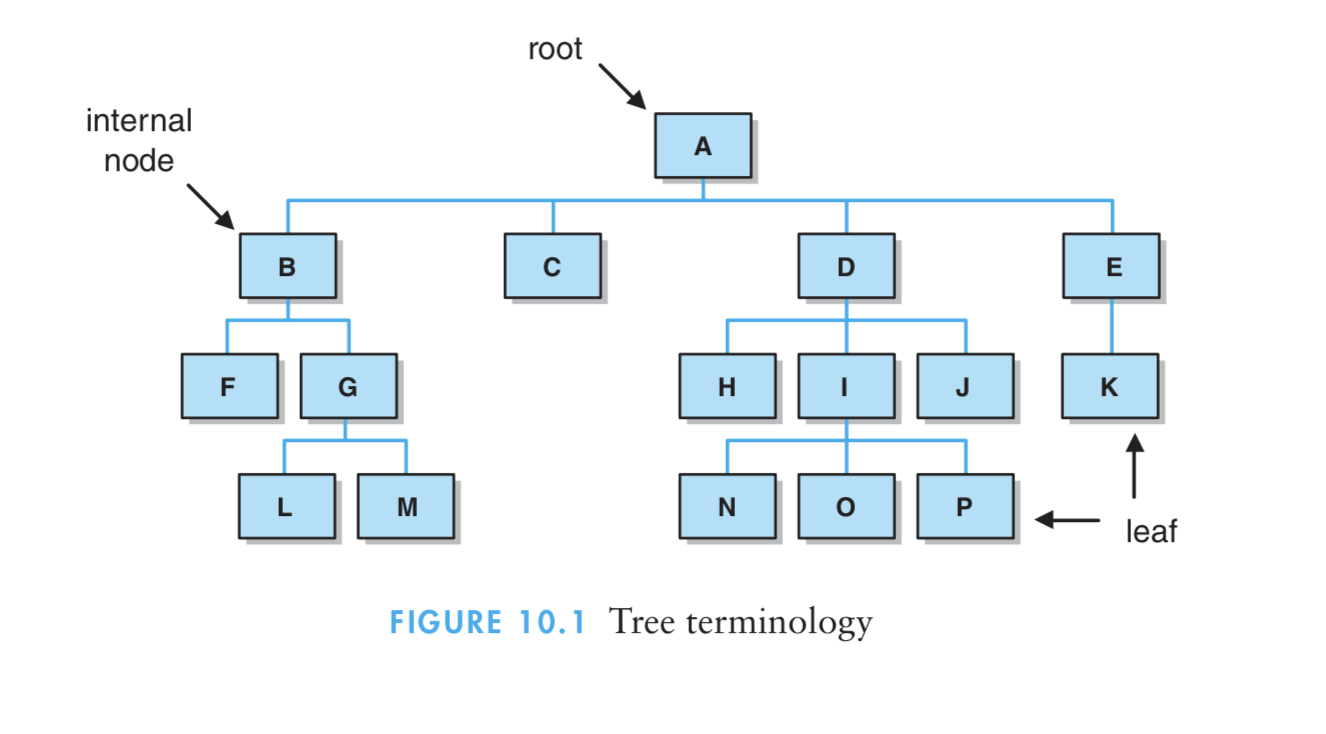
6、根结点是树中唯一一个没有双亲的结点。没有任何孩子的结点称为叶子。一个至少有一个孩其实自某一特定结点的路径可以子的非根结点称为一个内部结点。
7、沿着起始自某一特定结点的路径可以到达的结点是该结点的子孙。
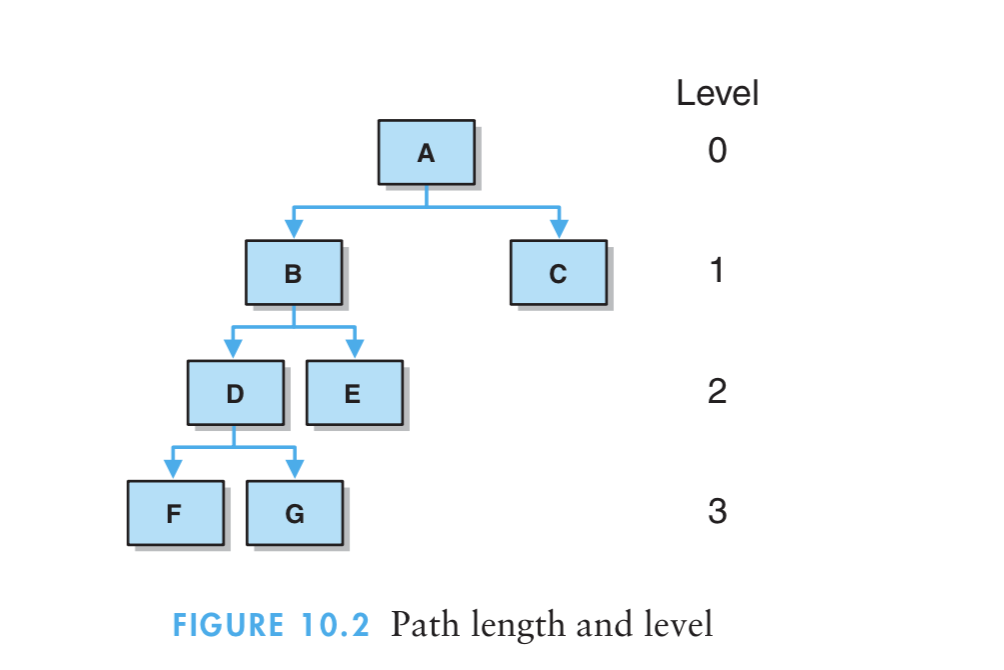
8、结点的层也就是从根结点到该结点的长度。通过计算从根到该结点所必须越过的边数目,就可以确定其路径长度。
二、树的分类
1、对结点所含有的孩子数目无限制的树称为广义树。
2、我们将每一结点限制为不超过n个孩子的树称为一颗n元树。
3、结点最多具有两个孩子的树称为二叉树。(注:含有m个元素的平衡n元树具有的高度为lognm。因此一颗含有n个结点的平衡二叉树具有的高度为log2m)
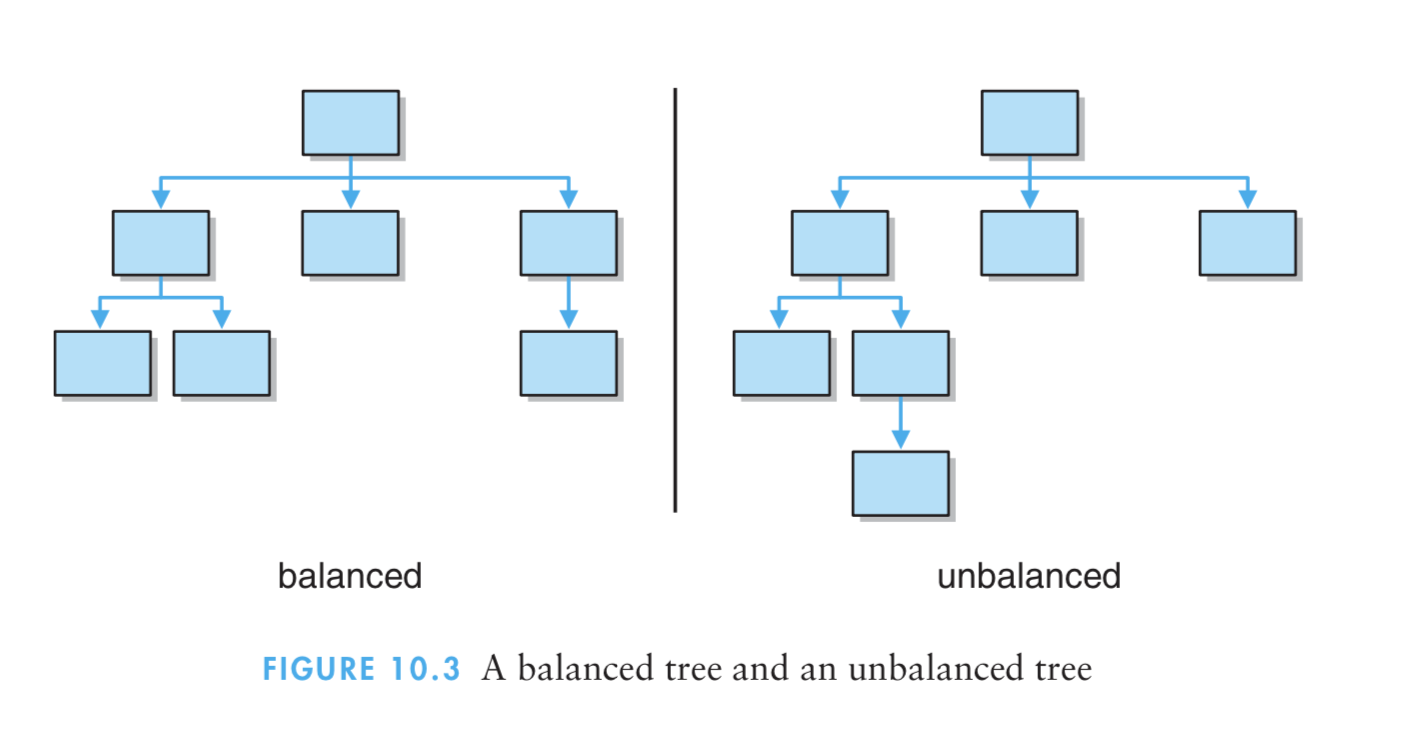
- 4、完全树:如果某树是平衡的,且底层所有叶子都位于树的左边,则认为该树是完全的。(注:完全二叉树在每个k层上都具有2^k个结点,最后一层除外,在最后一层中的结点必须是最左边的结点。)
- 5、满树:如果一颗n元的所有的叶子都位于同一层且每一结点要么是一片叶子要么正好是具有n个孩子,则称为此树是满的。
二、实现树的策略
1、树的数组实现之计算策略:
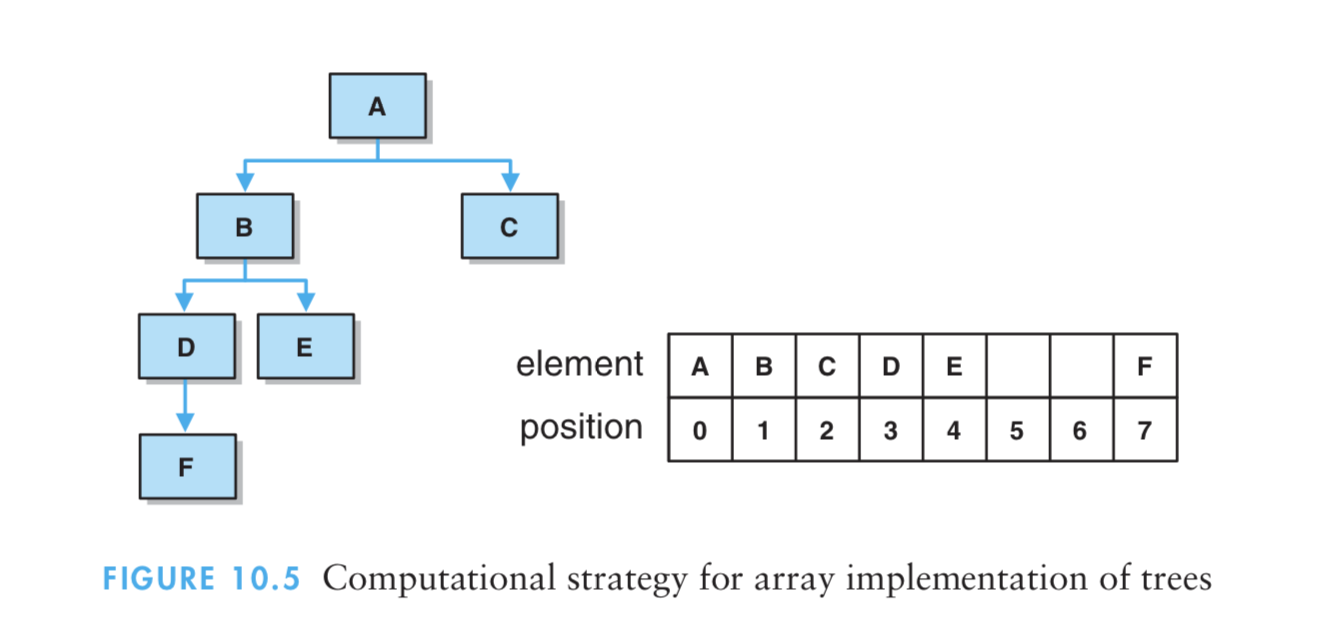
- 一种策略试试用数组来进行存储一棵树:对于任何储存在数组位置n处的元素而言,该元素的左孩子将存储在位置(2✖️n➕1)处,该元素的右孩子则存储在位置(2✖️(n➕1))处。
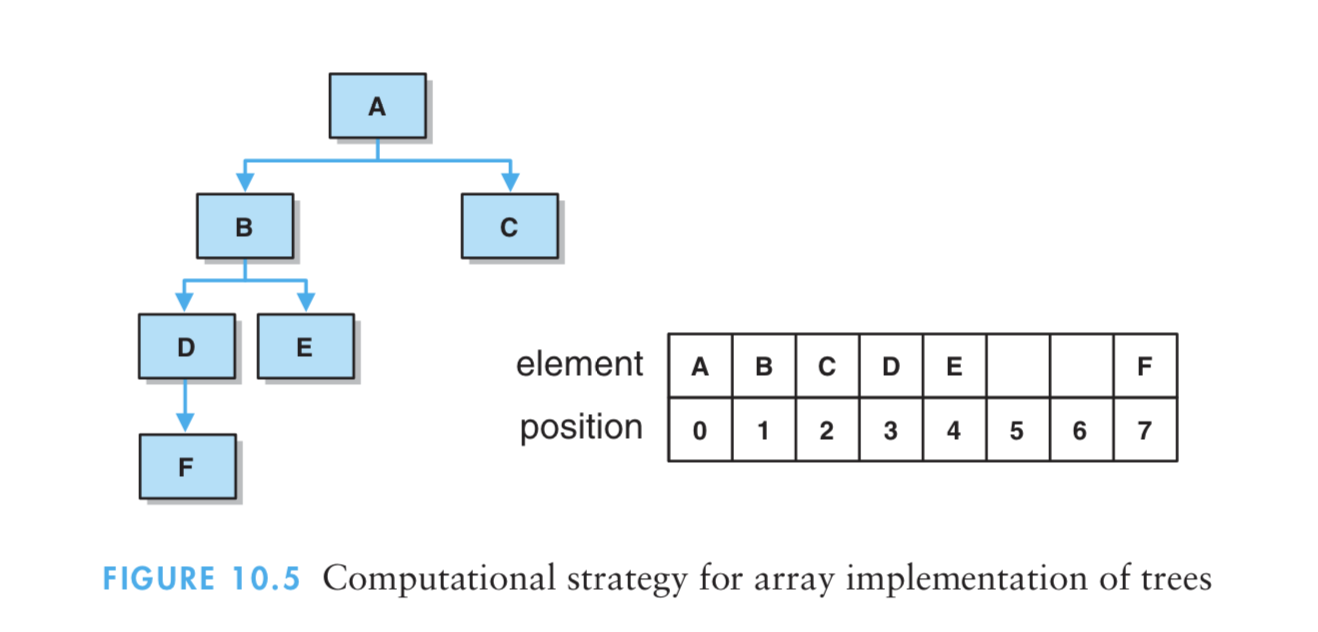
- 一种策略试试用数组来进行存储一棵树:对于任何储存在数组位置n处的元素而言,该元素的左孩子将存储在位置(2✖️n➕1)处,该元素的右孩子则存储在位置(2✖️(n➕1))处。
2、树的数组实现之模拟链接策略
模拟了操作系统管理内存的方式。按照先来先服务的基准连续分配数组位置,而不是通过其在树中的定位将数元素指派到数组位置上。
模拟链接策略允许连续分配数组位置而不用考虑该树的完全性。
3、树的分析
(1)树是实现其他集合的有用而且有效的方式。
(2)一般而言,一颗含有m个元素的平衡n元树具有的高度为lognm。
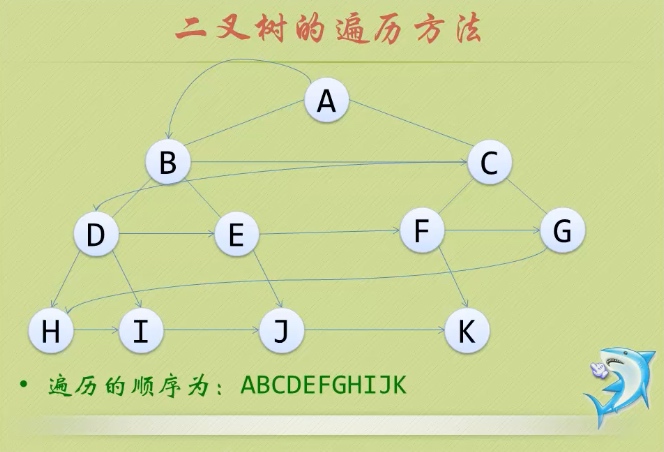
三、树的遍历
1、前序遍历(preorder traversal)
(1)顺序:从根结点开始,访问每一结点机及其孩子。
(2)图解:
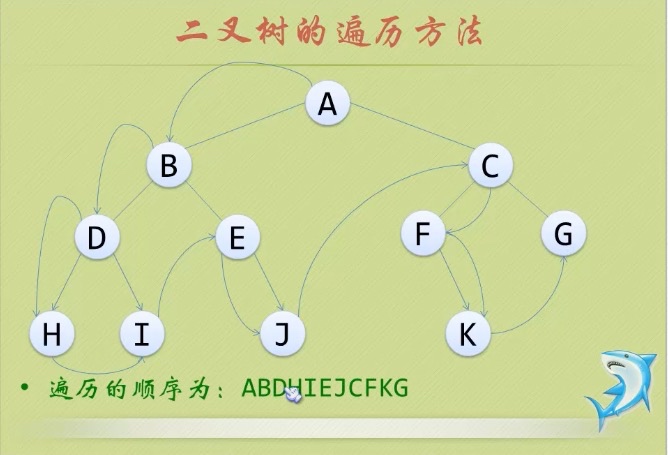
2、中序遍历(inorder traversal)
(1)顺序:从根结点开始,访问结点的左孩子,然后是该结点,再然后是任何剩余结点。
(2)图解:
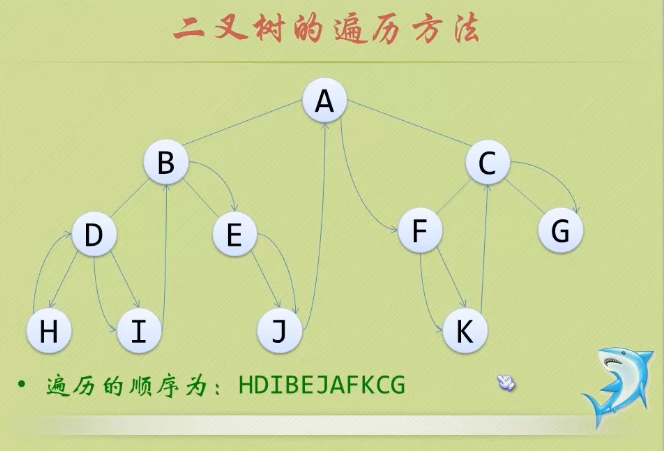
3、后序遍历(postorder traversal)
(1)从根结点开始,访问结点的孩子,然后是该结点。
(2)图解:
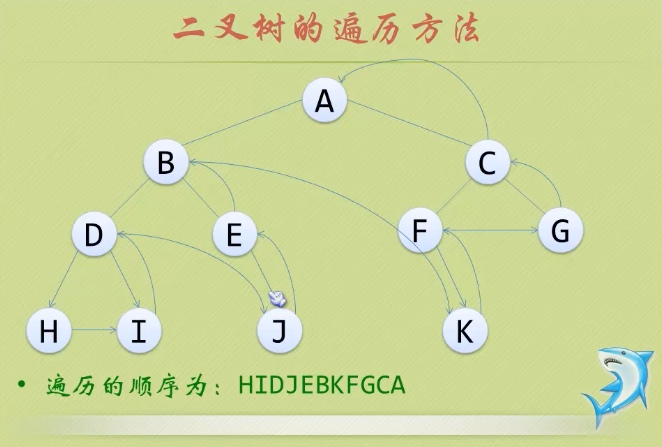
4、层序遍历(lever-order traversal)
(1)从根结点开始,访问每一层所有的结点,一次一层。
(2)图解:
四、二叉树
- 1、ADT:
| 操作 | 描述 |
|---|---|
| getRoot | 返回指向二叉树根的引用 |
| isEmpty | 判定该树是否为空 |
| size | 判定树中数量 |
| contains | 判定指针目标是否在该树中 |
| find | 如果找到该指定元素,则返回指向其的引用 |
| toString | 返回树的字符串表示 |
| iteratorInOrder | 为树的中序遍历返回一个迭代器 |
| iteratorPreOrder | 为树的前序遍历返回一个迭代器 |
| iteratorPostOrder | 为树的后序遍历返回一个迭代器 |
| iteratorLeverOrder | 为树的层序遍历返回一个迭代器 |
2、用链表实现二叉树
- (1)注:每个构造函数必须具有root和count属性。
3、二叉树的性质:
(1)性质1:在二叉树的第 i 层上至多有 2^(i-1)个结点 (i >=1)
(2)性质2:深度为 k 的二叉树至多有2^k -1个结点(k>=1)
(3)性质3:对任何一棵二叉树 T ,如果其终端结点数位n0,度为2的结点数位n2,则n0=n2+1。
注:
(1) n = n0 + n1 + n2 (结点总数 等于 度为0 加 度为1 加 度为2)
(2) n = n0 + 2*n2 +1(n = 分支总数+1 ;分支总数 = n1+n2 (分支是由度为1,度为2的结点射出的))
(3)-(1)得: n0 = n2 + 1
教材学习中的问题和解决过程
- 问题1:在书中有这样一句话:
最后一层除外,在最后一层中的结点必须是最左边的结点。
一开始我并没有特别理解这个意思是什么,因为我的第一意识就是我觉得最后一层都除外了,还提最后一层做什么?
问题1解决方案:
在昨天听了老师讲的课以后就知道他所说的是倒数第二层的结点必须是最左边的结点,这里也就引进了平衡树的概念。
那什么是平衡树呢?
1、平衡树:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
2、性质:最小二叉平衡树的节点的公式如下 F(n)=F(n-1)+F(n-2)+1

问题2:在学习使用二叉树:表达式树的时候,有这样一段代码让我很是纠结:
public boolean isOperator()
{
return (termType == 1);
}
它的实现在下面
if (temp.isOperator())
{
operand1 = evaluateNode(root.getLeft());
operand2 = evaluateNode(root.getRight());
result = computeTerm(temp.getOperator(), operand1, operand2);
}
else
result = temp.getValue();
}
就是temp到底是一个什么类型的值,它如何左右与1和其他之间字符?
问题2解决方法:
对于我自己是这样理解的:首先temp.isOperator()这句的作用就是在判断temp是否是一个操作符,我自己觉得termType == 1只是一个媒介,无论它是否是1都无所谓,那个1只是用于判断是否为一个数字,假如不为一个数字,就判断其为一个操作符,假如是操作数的话,就进行继续递归,继续重复。问题3:因为在学习表达式树的时候就在如何输出一个数存在着疑问,书本里的代码繁琐,让人很难看下去,为什么有契机写这个问题,是因为看了侯泽洋同学的博客以后,发现了他很是仔细的写了每一步的过程,然而我也因为当时自己代码实现过程中的一点问题,bug了两遍这一段程序,也了解到大致(后面会写到那个自己犯的傻瓜问题),在这里也进行一点记录。
问题3解决方法:
(1)首先我们从打的包中看到了我们这个方法中用到了四个类,包括之前写过的一个和本章需要完善的三个,如下
import chapter10.jsjf.BinaryTreeNode;
import chapter10.jsjf.LinkedBinaryTree;
import chapter6.练习题.pp6_8.ArrayUnorderedList;
import chapter6.练习题.pp6_8.UnorderedListADT;
(2)其次我们先要了解整个输出的过程,假如要输出一棵树的话,就得有它的形状,即如何控制我们所需要的空格,在我自己的计算中,和书中进行了统一,假如一棵树的层数有k层的话,就是在第0层第一个元素之前有2^k个空格" ";
然后当我们判断输出第0层了以后就通过1个或者2个\n进行换行,(ps:两个会好看一点,就和书中代码一样),进行判断就需要我们将元素和字符分别存入两个链表中,因为在我bug的时候发现一个问题,就是经常做的一个操作就是将链表进行头删,返回头删的值,这一操作为的是返回删除的值进行比较,选择是否进入判断语句。然后换行以后,进行同样的空格,假如遇到元素就要开始进行输出,转至(3)。进行新的空格计算,也就是2^(k-1),这个空格间距就是两个元素之间的空格数目。重复上述过程。
countNodes = countNodes + 1;
current = nodes.removeFirst();
currentLevel = levelList.removeFirst();
if (currentLevel > previousLevel)
{
result = result + "\n\n";
previousLevel = currentLevel;
for (int j = 0; j < ((Math.pow(2, (printDepth - currentLevel))) - 1); j++)
result = result + " ";
}
else
{
for (int i = 0; i < ((Math.pow(2, (printDepth - currentLevel + 1)) - 1)) ; i++)
{
result = result + " ";
}
}
(3)输出元素,包括空格和换行符我们都用一个result进行保存,以后再转至(2)结尾。
f (current != null)
{
result = result + (current.getElement()).toString();
nodes.addToRear(current.getLeft());
levelList.addToRear(currentLevel + 1);
nodes.addToRear(current.getRight());
levelList.addToRear(currentLevel + 1);
}
else {
nodes.addToRear(null);
levelList.addToRear(currentLevel + 1);
nodes.addToRear(null);
levelList.addToRear(currentLevel + 1);
result = result + " ";
}
}
代码调试中的问题和解决过程
问题1:在输出表达式树的时候,2和1的位置总是跑偏
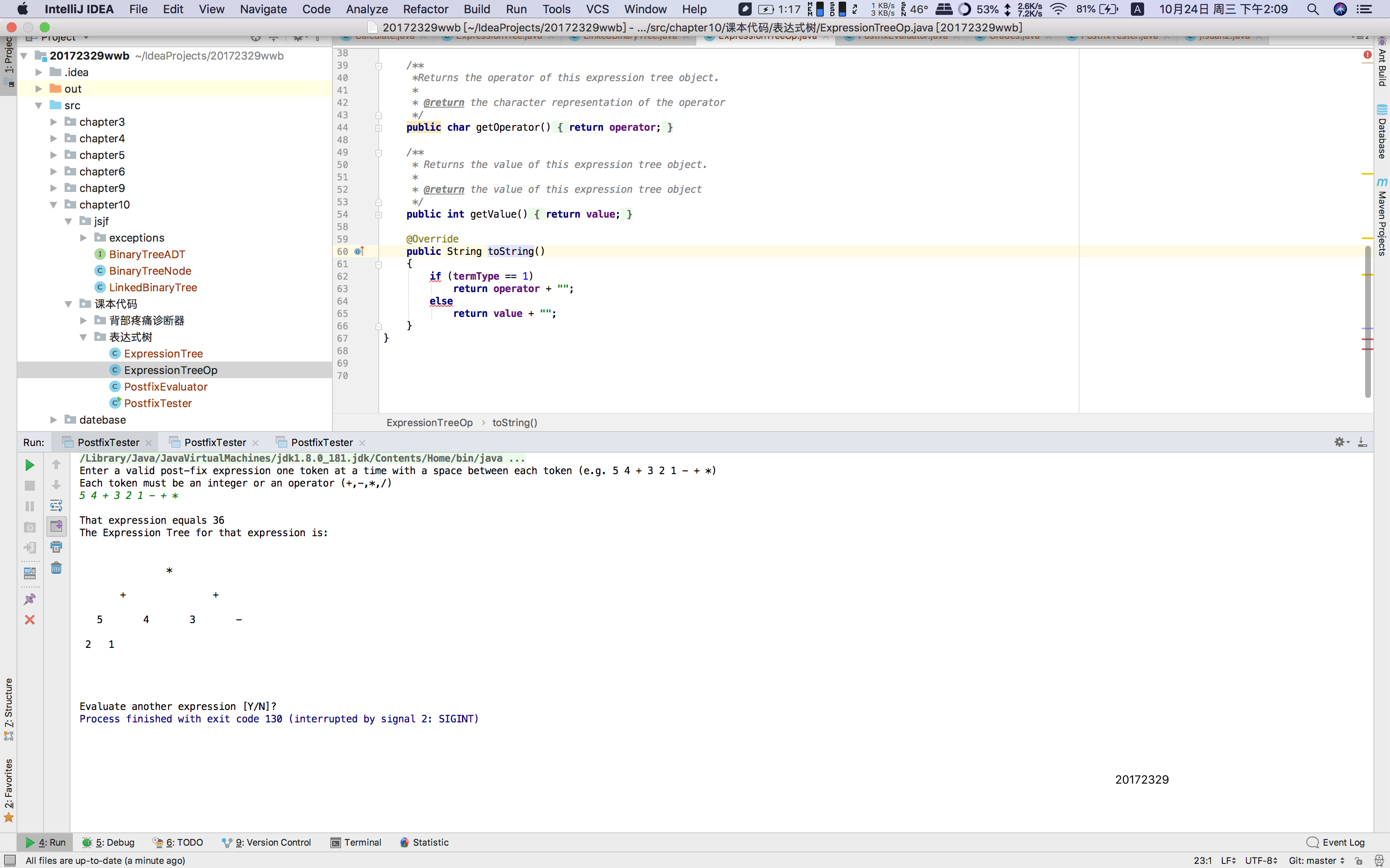
我可能花了3个小时一直bug找问题,但是就是找不到问题1解决:
我突然意识到可能自己之前写的添加方法不能用或者有错,就回去看了一眼,果真不出我所料。。
ps:之前写的大致是这样的:
就是用了一个while循环,找到最后一个添加进去,最后发现,自己有毒,有个rear不用,总是想着找最后一个,肯定是链表敲多了,自己都发现自己被链表已经深深的洗脑2018-2019-20172329 《Java软件结构与数据结构》第六周学习总结的更多相关文章
- 20172328 2018—2019《Java软件结构与数据结构》第二周学习总结
20172328 2018-2019<Java软件结构与数据结构>第二周学习总结 概述 Generalization 本周学习了第三章集合概述--栈和第四章链式结构--栈.主要讨论了集合以 ...
- 20172329 2018-2019《Java软件结构与数据结构》第一周学习总结
2018-2019-20172329 <Java软件结构与数据结构>第一周学习总结 在这学期就已经大二了,也已经步入了学习专业课的核心时间,在这个阶段,我们应该了解自己的学习情况,针对自己 ...
- 20172328 2018-2019《Java软件结构与数据结构》第一周学习总结
20172328 2018-2019<Java软件结构与数据结构>第一周学习总结 概述 Generalization 本周学习了软件质量.数据结构以及算法分析的具体内容,主要依托于所用教材 ...
- 20172328 2018-2019《Java软件结构与数据结构》第九周学习总结
20172328 2018-2019<Java软件结构与数据结构>第九周学习总结 概述 Generalization 本周学习了无向图.有向图.带权图.常用的图算法.图的实现策略. 教材学 ...
- 2018-2019-20172329 《Java软件结构与数据结构》第九周学习总结
2018-2019-20172329 <Java软件结构与数据结构>第九周学习总结 教材学习内容总结 <Java软件结构与数据结构>第十五章-图 一.图及无向图 1.图的相关概 ...
- 2018-2019-20172321 《Java软件结构与数据结构》第九周学习总结
2018-2019-20172321 <Java软件结构与数据结构>第九周学习总结 教材学习内容总结 第15章 图 无向图 图由顶点和边组成. 顶点由名字或标号来表示,如:A.B.C.D: ...
- 《JAVA软件结构与数据结构》第一周学习总结
学号 20172326 <JAVA软件结构与数据结构>第一周学习总结 教材学习内容总结 软件质量的几大特性 增长函数与大O记法 大O记法用来表示表示增长函数,从而来表示算法的复杂度 算法的 ...
- 2018-2019-20172329 《Java软件结构与数据结构》第二周学习总结
2018-2019-20172329 <Java软件结构与数据结构>第二周学习总结 教材学习内容总结 <Java软件结构与数据结构>第三章 集合概述--栈 一.集合 1.我们印 ...
- 20172305 2018-2019-1 《Java软件结构与数据结构》第二周学习总结
20172305 2018-2019-1 <Java软件结构与数据结构>第二周学习总结 教材学习内容总结 本周内容主要为书第三章和第四章的内容: 第三章(以数组来替代栈的作用) 集合(聚集 ...
- 20172305 2018-2019-1 《Java软件结构与数据结构》第九周学习总结
20172305 2018-2019-1 <Java软件结构与数据结构>第九周学习总结 教材学习内容总结 本周内容主要为书第十五章内容: 图(结点和结点之间的连接构成) 顶点:结点 边:结 ...
随机推荐
- nagios 在nrpe中自定义脚本
监控第三方端口(22000) #!/bin/bash#author:xiaoweige#check 140 22000 result=`sleep 1|telnet 10.2.1.140 22000| ...
- QoS policy-map class-map
QoS(Quality of ServiceQoS(Quality of Service,服务质量)指一个网络能够利用各种基础技术,为指定的网络通信提供更好的服务能力, 是网络的一种安全机制, 是用来 ...
- ABAP术语-Authorization Profile
Authorization Profile 原文:http://www.cnblogs.com/qiangsheng/archive/2007/12/21/1008992.html Element o ...
- Mac设置信认任意来源应用
升级了Mac 10.13.4 后应用软件各种不适配,最近更新了一个应用版本,在去安全设置里面 信任应用的时候,发现"任何来源"这个选项不见了!不见了!WTF! 接下来,我们就打开终 ...
- winform 自定义控件:半透明Loading控件
winform 自定义控件:半透明Loading控件 by wgscd date:2015-05-05 效果: using System;using System.Drawing;using Sys ...
- RabbitMQ(四):RPC的实现
原文:RabbitMQ(四):RPC的实现 一.RPC RPC(Remote Procedure Call)—远程过程调用,它是一种通过网络从远程计算机程序上请求服务,而不需要了解底层网络技术的协议. ...
- [COCI2009]Dvapravca 计算几何
[COCI2009]Dvapravca LG传送门 先给出考场上的\(O(n^3)\)乱搞方法:枚举一个蓝点和一个红点,找出过着两个点的直线,再枚举蓝点找出这条直线最多能往两边扩展多宽,最后枚举红点计 ...
- 传统路由和OVS区别
本文主要描述了一种将三层路由变成二层交换转发(以及二层转发变成三层路由)的实现方式,以应对OVS(OpenFlow)跨网段路由复杂的问题:当然技术本身是客观的,具体应用还要看场景. 随着SDN技术不断 ...
- 洛咕 P3964 [TJOI2013]松鼠聚会
有个结论就是把坐标\((x,y)\)变形成\(((x+y)/2,(x-y)/2)\),切比雪夫距离就变成了曼哈顿距离. 所以变换一下坐标直接统计答案即可. // luogu-judger-enable ...
- linux提权 searchsploit 使用规范
使用 searchsploit 时,要把整个控制台最大化,这样才能显示完整的漏洞信息. 查看漏洞帮助文件:
- 20172328 2018—2019《Java软件结构与数据结构》第二周学习总结
