时间复杂度 NOIP_2017_D1T2

　　

　　有的题做了很久\感想比较深\可以引申很多\上台讲过,所以单开一篇，不放在总结下面。

　　这道题做的时候花了很长时间，犯的错也比较典型，当时写过一篇单独的总结，放在学校了，返校后粘上来。

　　

时间复杂度

　　小明正在学习一种新的编程语言 A++，刚学会循环语句的他激动地写了好多程序并 给出了他自己算出的时间复杂度，可他的编程老师实在不想一个一个检查小明的程序， 于是你的机会来啦！下面请你编写程序来判断小明对他的每个程序给出的时间复杂度是否正确。

　　A++语言的循环结构如下：

　　F i x y

　　循环体

　　E

　　其中F i x y表示新建变量 i （变量 i 不可与未被销毁的变量重名）并初始化为 x ， 然后判断 i 和 y 的大小关系，若 i 小于等于 y 则进入循环，否则不进入。每次循环结束后 i 都会被修改成 i +1，一旦 i 大于 y 终止循环。

　　 x 和 y 可以是正整数（ x 和 y 的大小关系不定）或变量 n 。 n 是一个表示数据规模的变量，在时间复杂度计算中需保留该变量而不能将其视为常数，该数远大于 100。

　　“E”表示循环体结束。循环体结束时，这个循环体新建的变量也被销毁。

　　注：本题中为了书写方便，在描述复杂度时，使用大写英文字母“O”表示通常意义下“Θ”的概念。

　　输入文件第一行一个正整数 t ，表示有 t （ t<=10 ）个程序需要计算时间复杂度。 每个程序我们只需抽取其中 F i x y和E即可计算时间复杂度。注意：循环结构 允许嵌套。

接下来每个程序的第一行包含一个正整数 L 和一个字符串， L 代表程序行数，字符 串表示这个程序的复杂度，O(1)表示常数复杂度，O(n^w)表示复杂度为 n^w，其 中w是一个小于100的正整数（输入中不包含引号），输入保证复杂度只有O(1)和O(n^w) 两种类型。

　　接下来 L 行代表程序中循环结构中的F i x y或者 E。 程序行若以F开头，表示进入一个循环，之后有空格分离的三个字符（串）i x y， 其中 ii 是一个小写字母（保证不为 nn ），表示新建的变量名， x 和 y 可能是正整数或 n ，已知若为正整数则一定小于 100。

　　程序行若以E开头，则表示循环体结束。

---

　　模拟题。

　　多组数据，要记得清空数组。

　　首先读入行数以及std的时间复杂度。

　　第一次做的时候发现std的复杂度可能不是一位数，然而还是处理错了，最坑的是对于小数据的处理是完全没有问题的，只有在数据达到一定程度时才能看出来，所以以后编程时写好一部分就要先测试，比如说这道题的std，编写完就应该测试各种情况如O(1),O(n^1),O(n^99)之类的情况，而不是等全写完了之后再改，很容易出错。一开始写的两位数处理中十位和个位是反的。。。。。。

　　正确的代码如下：

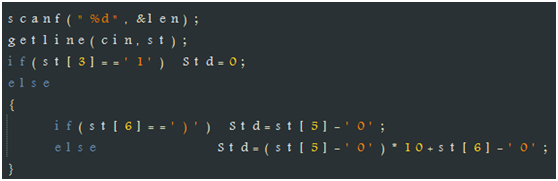
　　接着读入程序的每一行，先判断是否有语法错误，这一块感觉很难，其实却是最简单的部分。

1. 变量冲突：维护一个栈，存放目前每一层的循环变量，当循环结束时将本层的循环变量销毁。如果某个变量当前正在被使用，又有新的变量要用同样的变量名，这个程序就出现了语法错误。
2. 开始与结束不匹配：每读到一个F开头的句子，栈的深度+1，读到E开头的句子，深度-1。如果深度在某一次被减到＜0了，证明语法错误，如果程序结束了深度却不为0，也是错的。

　　最后再计算时间复杂度。

　　这一块是最复杂的，每一层的时间复杂度等于本层的复杂度加上下一层中复杂度最大的一个，在dep层结束时再更新dep+1层的复杂度，否则会出错，注意，如果本层根本就不执行，它的时间复杂度一定是0，而不能再加上下一层的复杂度。这一部分其实一开始也想到了，但是改着改着就给忘了，以后做这种大模拟如果想到什么细节就写在纸上，到最后提交前再检查一下，因为边写边改的话过一会就忘了这一句有什么用，可能不小心就删了。

　　现在就只剩下计算本层的时间复杂度了。

　　除去循环变量和F,开始和结束共有9种情况：

　　

F		i		n		n
F		i		n		1
F		i		n		1	2
F		i		1		n
F		i		1		1
F		i		1		1	2
F		i		1	2		n
F		i		1	2		1
F		i		1	2		1	2

　　如果是n，就用-1表示。

　　　　

如果be和en相等，常数复杂度；

如果be是n，en是常数，不执行；

如果en是常数，be是n，n的复杂度；

如果en和be都是常数：be<=en，常数复杂度；

如果be>en，不执行。

# include <cstdio>
# include <iostream>
# include <cstring>
# include <cstring>

using namespace std;

int t,len,nl,Std,dep;
string st,pr[];
bool uke,f,vis[]={};
int sta[],maxa[];
int ans[],F[];

void ac()
{
    for (int i=;i<=len;i++)
    {
        if(pr[i][]=='F')
        {
            dep++;
            sta[dep]=pr[i][]-'a';
            if (vis[sta[dep]]) uke=true;
            vis[sta[dep]]=true;
        }
        else
        {
            if(dep==) uke=true;
            vis[sta[dep]]=false;
            dep--;
        }
    }
    if(dep!=) uke=true;
    return ;
}

bool wa()
{
    memset(maxa,,sizeof(maxa));
    string no;
    int be,en;
    for (int i=;i<=len;i++)
    {
        if(pr[i][]=='F')
        {
            dep++;
            no=pr[i];
            int ss=;
            if(no[]=='n')
            {
                be=-;
                if(no[]=='n') en=-;
                else if(no[]>=''&&no[]<='') en=(no[]-'')*+no[]-'';
                else en=no[]-'';
            }
            else if(no[]==' ')
            {
                be=no[]-'';
                if(no[]=='n') en=-;
                else if(no[]>=''&&no[]<='') en=(no[]-'')*+no[]-'';
                else en=no[]-'';
            }
            else
            {
                be=(no[]-'')*+no[]-'';
                if(no[]=='n') en=-;
                else if(no[]>=''&&no[]<='') en=(no[]-'')*+no[]-'';
                else en=no[]-'';
            }
            if(be==en)
                ss=;
            else if(be==-)
                ss=-;
            else if(en==-)
                ss=;
            else if(be<=en)
                ss=;
            else
                ss=-;
            ans[dep]=ss;
        }
        else
        {
            if(ans[dep]!=-) ans[dep]+=maxa[dep];
            maxa[dep-]=max(maxa[dep-],ans[dep]);
            ans[dep]=;
            maxa[dep]=;
            dep--;
        }
    }
    if(maxa[]==Std) return true;
    return false;
}

int main()
{
    scanf("%d",&t);
    for (int shzr=;shzr<=t;shzr++)
    {
        scanf("%d",&len);
        getline(cin,st);
        if(st[]=='') Std=;
        else
        {
            if(st[]==')') Std=st[]-'';
            else          Std=(st[]-'')*+st[]-'';
        }
        memset(vis,,sizeof(vis));
        memset(ans,,sizeof(ans));
        memset(F,,sizeof(F));
        uke=f=false;
        for (int i=;i<=len;i++)
            getline(cin,pr[i]);
        dep=;
        ac();
        if(uke) printf("ERR\n");
        else
        {
            dep=;
            if(wa()) printf("Yes\n");
            else       printf("No\n");
        }
    }
    return ;
}

时间复杂度

终于写完啦qwq。

---shzr