POJ 3468 A Simple Problem with Integers （区间更新+区间查询）

题目链接

Description

You have N integers, A1, A2, ... , AN. You need to deal with two kinds of operations. One type of operation is to add some given number to each number in a given interval. The other is to ask for the sum of numbers in a given interval.

Input

The first line contains two numbers N and Q. 1 ≤ N,Q ≤ 100000.

The second line contains N numbers, the initial values of A1, A2, ... , AN. -1000000000 ≤ Ai ≤ 1000000000.

Each of the next Q lines represents an operation.

"C a b c" means adding c to each of Aa, Aa+1, ... , Ab. -10000 ≤ c ≤ 10000.

"Q a b" means querying the sum of Aa, Aa+1, ... , Ab.

Output

You need to answer all Q commands in order. One answer in a line.

Sample Input

10 5

1 2 3 4 5 6 7 8 9 10

Q 4 4

Q 1 10

Q 2 4

C 3 6 3

Q 2 4

Sample Output

4

55

9

15

分析：

首先不考虑原始的情况，我们只考虑区间更新过后带来的影响的话，首先对于询问一个区间当中的元素和的话，肯定就是这个区间的原始的元素和，加上区间更新后所带来的影响，所以我们用a[]数组来保存前i个元素的和。

然后考虑区间更新所带来的影响，采用差分的思想，

设原数组第i位的值为ai，di=ai−a[i−1]，则有(这里认为a0=0，此时的a表示的是数组中的原始值，与代码中的a不一样)：

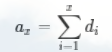
所以有：

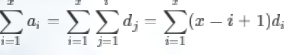
于是我们得到了：

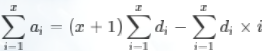
于是我们把原数组差分后维护两个树状数组，一个维护di，一个维护di×i。

这样区间求和时可以在两个树状数组中查询得到前缀和，区间修改时就是差分数组的修改，每次修改两个点即可。

其中c[i]维护的是d[i]，c1[i]维护的是d[i]×i。

但是这里的c[]和c1[]都是差分数组，保存的也就只是更新所带来的值的变化，但因为这里要求的是在原来的基础上更新后的区间和，所以最终还要加上最原始的区间和。

代码：

#include<stdio.h>
#include<iostream>
#include<string.h>
using namespace std;
long long int a[510000],c[510000],c1[510000];
int n,k;
int lowbit(int x)
{
    return x&(-x);
}
void update(long long int x,long long int val)
{
    for(int i=x; i<=n; i+=lowbit(i))
    {
        c[i]+=val;
        c1[i]+=(long long)x*val;   //给差分数组中的位置x加上y
    }
}
long long sum(long long int x) //查询前x项的和
{
    long long ans=0;
    for(int i=x; i; i-=lowbit(i))
        ans+=(x+1)*c[i]-c1[i];
    return ans+a[x];
}

int main()
{
    char ch;
    long long int st,ed,val,num;
    while(~scanf("%d%d",&n,&k))
    {
        memset(a,0,sizeof(a));
        memset(c,0,sizeof(c));
        memset(c1,0,sizeof(c1));
        for(int i=1; i<=n; i++)
        {
            scanf("%lld",&num);
            a[i]+=a[i-1]+num;//a[i]保存的是前i个数的和
        }
        for(int i=0; i<k; i++)
        {
            getchar();
            scanf("%c",&ch);
            if(ch=='Q')
            {
                scanf("%llld%lld",&st,&ed);
                printf("%lld\n",sum(ed)-sum(st-1));
            }
            else
            {
                scanf("%lld%lld%lld",&st,&ed,&val);
                update(st,val);
                update(ed+1,-val);
            }
        }
    }
    return 0;
}