Pythagorean Triples 707C

Katya studies in a fifth grade. Recently her class studied right triangles and the Pythagorean theorem. It appeared, that there are triples of positive integers such that you can construct a right triangle with segments of lengths corresponding to triple. Such triples are called Pythagorean triples.

For example, triples (3, 4, 5), (5, 12, 13) and (6, 8, 10) are Pythagorean triples.

Here Katya wondered if she can specify the length of some side of right triangle and find any Pythagorean triple corresponding to such length? Note that the side which length is specified can be a cathetus as well as hypotenuse.

Katya had no problems with completing this task. Will you do the same?

Input

The only line of the input contains single integer n (1 ≤ n ≤ 109) — the length of some side of a right triangle.

Output

Print two integers m and k (1 ≤ m, k ≤ 1018), such that n, m and k form a Pythagorean triple, in the only line.

In case if there is no any Pythagorean triple containing integer n, print  - 1 in the only line. If there are many answers, print any of them.

Examples

input

Copy

3

output

Copy

4 5

input

Copy

6

output

Copy

8 10

input

Copy

1

output

Copy

-1

input

Copy

17

output

Copy

144 145

input

Copy

67

output

Copy

2244 2245

Note

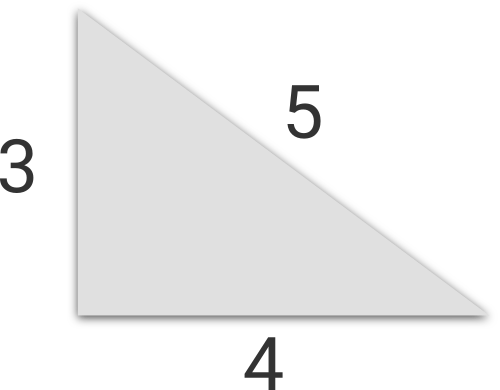
Illustration for the first sample.

题意：给你一条直角边，让你求出另一条直角边与斜边，如果没有，则输出-1

分析：a²+b²=c²,a²=(c-b)(c+b),如果a是奇数,c-b=1,c+b=a*a，c=a*a+1/2, b=c-1.如果a是偶数，先判断，1：如果不断的除2，是否是奇数，是奇数就执行c=a*a+1/2, b=c-1；2：当其不断除2等于4时，执行c=5,b=3;

 #include<cstdio>
 int main()
 {
     long long n;
     while(~scanf("%lld",&n))
     {
         long long b,c;
         if(n%!=)//当直角边时奇数的时候直接执行
         {
             b=(n*n-)/;
             c=b+;
             if(b==)
                 printf("-1\n");
             else
             printf("%lld %lld\n",b,c);
         }
         else//当直角边是偶数的时候
         {
             long long t=;
             while()
             {
                 if(n==)
                     break;
                 if(n%!=)
                     break;
                 n/=;
                 t*=;

             }//不断除2，看其是否为奇数，或者不断除2等于4
             if(n==)
             {
                 b=;
                 c=;
                 b*=t;
                 c*=t;
             }//如果等于4就满足，a=,b=,a=5的情况
             else
             {
             b=(n*n-)/;
             c=b+;
             b*=t;
             c*=t;
             }//否则就满足a是奇数的情况
             if(b==)
                 printf("-1\n");
             else
             printf("%lld %lld\n",b,c);
         }
     }
     return ;
 }