【ZJOI2015】诸神眷顾的幻想乡解题报告

【ZJOI2015】诸神眷顾的幻想乡

Description

幽香是全幻想乡里最受人欢迎的萌妹子，这天，是幽香的2600岁生日，无数幽香的粉丝到了幽香家门前的太阳花田上来为幽香庆祝生日。

粉丝们非常热情，自发组织表演了一系列节目给幽香看。幽香当然也非常高兴啦。

这时幽香发现了一件非常有趣的事情，太阳花田有$n$块空地。在过去，幽香为了方便，在这$n$块空地之间修建了$n-1$条边将它们连通起来。也就是说，这n块空地形成了一个树的结构。

有$n$个粉丝们来到了太阳花田上。为了表达对幽香生日的祝贺，他们选择了$c$中颜色的衣服，每种颜色恰好可以用一个$0$到$c-1$之间的整数来表示。并且每个人都站在一个空地上，每个空地上也只有一个人。这样整个太阳花田就花花绿绿了。幽香看到了，感觉也非常开心。

粉丝们策划的一个节目是这样的，选中两个粉丝$A$和$B$（$A$和$B$可以相同），然后$A$所在的空地到$B$所在的空地的路径上的粉丝依次跳起来（包括端点），幽香就能看到一个长度为$A$到$B$之间路径上的所有粉丝的数目（包括$A$和$B$）的颜色序列。一开始大家打算让人一两个粉丝（注意：$A,B$和$B,A$是不同的，他们形成的序列刚好相反，比如红绿蓝和蓝绿红）都来一次，但是有人指出这样可能会出现一些一模一样的颜色序列，会导致审美疲劳。

于是他们想要问题，在这个树上，一共有多少可能的不同的颜色序列（子串）幽香可以看到呢？

太阳花田的结构比较特殊，只与一个空地相邻的空地数量不超过$20$个。

Input

第一行两个正整数$n,c$。表示空地数量和颜色数量。

第二行有$n$个$0$到$c-1$之间，由空格隔开的整数，依次表示第$i$块空地上的粉丝的衣服颜色。（这里我们按照节点标号从小到大的顺序依次给出每块空地上粉丝的衣服颜色）。

接下来$n-1$行，每行两个正整数$u,v$，表示有一条连接空地$u$和空地$v$的边。

Output

一行，输出一个整数，表示答案。

Sample Input

7 3

0 2 1 2 1 0 0

1 2

3 4

3 5

4 6

5 7

2 5

Sample Output

HINT

对于所有数据，$1\le n\le 100000, 1\le c\le 10$。

对于$15\%$的数据，$n\le 2000$。

另有$5\%$的数据，所有空地都至多与两个空地相邻。

另有$5\%$的数据，除一块空地与三个空地相邻外，其他空地都分别至多与两个空地相邻。

另有$5\%$的数据，除某两块空地与三个空地相邻外，其他空地都分别至多与两个空地相邻

压根没搞懂什么是对的广义SAM，什么是错的广义SAM，我的代码说不定是假的。

具体思路，直接对每个度为1的点建广义SAM，就是每次处理的las是原树父亲节点建出的那个点要处理，其他和SAM一样。直接把所有点的广义SAM建到一起就行了。

感觉还是要看统计的是什么，大家可以看看这个数据

SAM长这个鬼样子

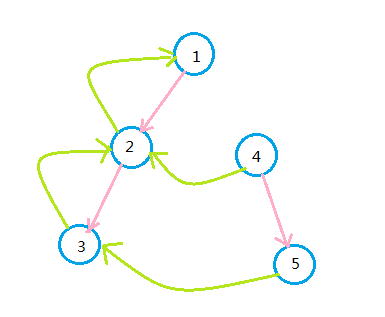
嗯，感觉这个len就很对了吧，虽然感觉状态一样的节点很诡异

Code:

#include <cstdio>

#include <cstring>

#define ll long long

const int N=1e5+10;

const int M=4e6+10;

int ch[M][10],len[M],par[M],tot=1;

int in[N],s[N];

int extend(int p,int c)

{

    int now=++tot;

    len[now]=len[p]+1;

    while(p&&!ch[p][c]) ch[p][c]=now,p=par[p];

    if(!p) par[now]=1;

    else

    {

        int x=ch[p][c];

        if(len[x]==len[p]+1) par[now]=x;

        else

        {

            int y=++tot;

            len[y]=len[p]+1,par[y]=par[x];

            memcpy(ch[y],ch[x],sizeof ch[x]);

            while(p&&ch[p][c]==x) ch[p][c]=y,p=par[p];

            par[now]=par[x]=y;

        }

    }

    return now;

}

int head[N],to[N<<1],Next[N<<1],cnt;

void add(int u,int v)

{

    to[++cnt]=v,Next[cnt]=head[u],head[u]=cnt;

}

void dfs(int now,int fa,int las)

{

    int bee=extend(las,s[now]);

    for(int v,i=head[now];i;i=Next[i])

        if((v=to[i])^fa)

            dfs(v,now,bee);

}

int main()

{

    int n,c;scanf("%d%d",&n,&c);

    for(int i=1;i<=n;i++) scanf("%d",s+i);

    for(int u,v,i=1;i<n;i++) scanf("%d%d",&u,&v),++in[u],++in[v],add(u,v),add(v,u);

    for(int i=1;i<=n;i++) if(in[i]==1) dfs(i,0,1);

    ll ans=0;

    for(int i=1;i<=tot;i++) ans=ans+len[i]-len[par[i]];

    printf("%lld\n",ans);

    return 0;

}

2019.1.10