BZOJ 4407 于神之怒加强版 (莫比乌斯反演 + 分块)

4407: 于神之怒加强版

Time Limit: 80 Sec  Memory Limit: 512 MB
Submit: 1067  Solved: 494
[Submit][Status][Discuss]

Description

给下N,M,K.求

 

 

Input

输入有多组数据，输入数据的第一行两个正整数T,K，代表有T组数据，K的意义如上所示，下面第二行到第T+1行，每行为两个正整数N,M，其意义如上式所示。

Output

如题

Sample Input

1 2
3 3

Sample Output

20

HINT

1<=N,M,K<=5000000,1<=T<=2000

题解：JudgeOnline/upload/201603/4407.rar

Source

命题人：成都七中张耀楠，鸣谢excited上传。

析：首先能看出来是莫比乌斯反演，直接求是单次O(n*sqrt(n))，肯定会TLE，然后进行两次分块，单次时间复杂度是O(n)，这样我本以为就能过了，结果还是TLE，实在是没想到好办法，就看了题解，题解是再进行化简，只要一次分块就好，其他的都进行预处理，单次询问复杂度是O(sqrt(n))。盗用一张图。

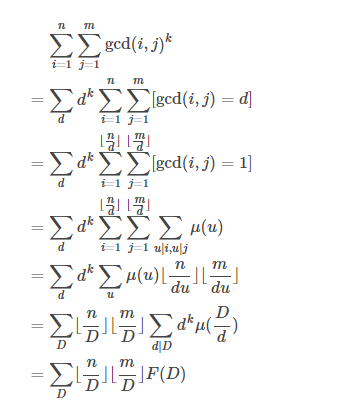
最后这个F函数是一个积性函数，可以用递推和筛法来求。

代码如下：

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <string>
#include <cstdlib>
#include <cmath>
#include <iostream>
#include <cstring>
#include <set>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <cctype>
#include <cmath>
#include <stack>
#include <sstream>
#include <list>
#include <assert.h>
#include <bitset>
#include <numeric>
#define debug() puts("++++")
#define gcd(a, b) __gcd(a, b)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define fi first
#define se second
#define pb push_back
#define sqr(x) ((x)*(x))
#define ms(a,b) memset(a, b, sizeof a)
#define sz size()
#define pu push_up
#define pd push_down
#define cl clear()
//#define all 1,n,1
#define FOR(i,x,n)  for(int i = (x); i < (n); ++i)
#define freopenr freopen("in.txt", "r", stdin)
#define freopenw freopen("out.txt", "w", stdout)
using namespace std;

typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> P;
const int INF = 0x3f3f3f3f;
const LL LNF = 1e17;
const double inf = 1e20;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int maxn = 5e6 + 5;
const int maxm = 3e5 + 10;
const LL mod = 1e9 + 7LL;
const int dr[] = {-1, 0, 1, 0};
const int dc[] = {0, -1, 0, 1};
const char *de[] = {"0000", "0001", "0010", "0011", "0100", "0101", "0110", "0111", "1000", "1001", "1010", "1011", "1100", "1101", "1110", "1111"};
int n, m;
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
inline bool is_in(int r, int c) {
  return r >= 0 && r < n && c >= 0 && c < m;
}

LL fast_pow(LL a, int n){
  LL res = 1;
  while(n){
    if(n&1)  res = res * a % mod;
    a = a * a % mod;
    n >>= 1;
  }
  return res;
}

LL f[maxn];
int prime[maxn];
bool vis[maxn];

void Moblus(int k){
  int tot = 0;
  f[1] = 1;
  for(int i = 2; i < maxn; ++i){
    if(!vis[i])  prime[tot++] = i, f[i] = fast_pow(i, k) - 1;
    for(int j = 0; j < tot && i * prime[j] < maxn; ++j){
      int t = i * prime[j];
      vis[t] = 1;
      if(i % prime[j] == 0){
        f[t] = f[i] * fast_pow(prime[j], k) % mod;
        break;
      }
      f[t] = f[i] * f[prime[j]] % mod;
    }
  }
  for(int i = 2; i < maxn; ++i)  f[i] = (f[i-1] + f[i]) % mod;
}

int main(){
  int T, k;  scanf("%d %d", &T, &k);
  Moblus(k);
  while(T--){
    scanf("%d %d", &n, &m);
    int mmin = min(n, m);
    LL ans = 0;
    for(int i = 1, det = 1; i <= mmin; i = det + 1){
      det = min(n/(n/i), m/(m/i));
      ans = (ans + (f[det] - f[i-1]) * (n/i) % mod * (m/i)) % mod;
    }
    printf("%lld\n", (ans+mod)%mod);
  }
  return 0;
}