USACO 2020 OPEN Favorite Colors【并查集-启发式合并-思考】

题目链接

题意简述

仰慕喜欢同色奶牛的奶牛喜欢同色 （禁止套娃 ，求一种方案，奶牛喜欢的颜色种数最多，多种方案求字典序最小。

题目解析

这道题我最先想到的居然是二分+并查集，我在想啥

咳咳

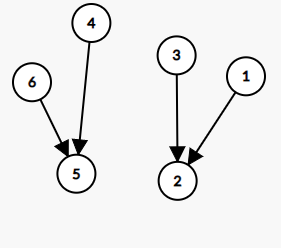
首先，考虑一个比较简单的情况，假如图长这样：

仰慕关系：\(6,4\)仰慕\(5\)，\(3,1\)仰慕\(2\)

同一头奶牛喜欢的颜色当然是相同的，\(6,4\)仰慕对象的喜好颜色一样，所以\(6,4\)喜欢的颜色一样，同理\(3,1\)喜欢的颜色一样。我们把他们用并查集套起来，数有几个块就可以了

然后考虑更复杂的情况：

如图，\(4\)是一只花心的奶牛，它不仅仰慕\(5\)，还仰慕\(2\)。

同一头奶牛喜欢的颜色当然是相同的，\(4\)只有一种喜欢的颜色，而\(6\)和\(4\)喜欢颜色一样，因为它们都喜欢\(5\)，同理，\(3,1\)喜好颜色也和\(4\)一样，那么两个连通块就通过\(4\)联通了。

为了方便写代码，我们这样看这个图：（就是把边反了个向，好写代码

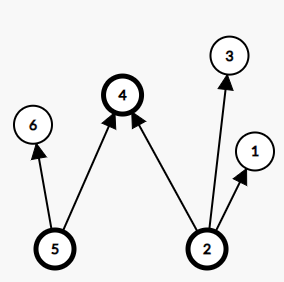
从两只站在仰慕链顶端的牛出发（其实也不一定是从它们出发，反正所有牛的儿子都要并在一起，话说也不一定有站在仰慕链顶端的牛，没有保证是\(DAG\)），把它们的儿子并在一起，如果碰到了\(4\)这样的花心结点，就把两个并查集合在一起。

至于原图，一个并查集里的点可以当成一个点来处理，也就是要缩点。具体的方法很暴力，就是把别人的儿子接到我这里来，然后把别人和它的儿子都从图里删掉。为了保障复杂度，用启发式合并，也就是小的集合合并到大集合上去。

---

►Code View

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
#define LL long long
#define N 200005
#define INF 0x3f3f3f3f
int rd()
{
	int x=0,f=1;char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1; c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48); c=getchar();}
	return f*x;
}
vector<int>G[N];
int n,m,f[N]/*连通块的大小 启发式合并要用到 初始为-1 表示自己是根*/,c[N];
int Find(int x)
{
	if(f[x]<0) return x;
	return f[x]=Find(f[x]);
}
void dfs(int u)
{
    if(G[u].size()<2) return ;
    int x=Find(G[u][0]);
    for(int i=1;i<G[u].size();i++)
	{
        int y=Find(G[u][i]);
        if(x==y)continue;
        if(f[x]<=f[y])
		{
            f[x]+=f[y];
            f[y]=x;
            for(int j=0;j<G[y].size();j++)
                G[x].push_back(G[y][j]);
            G[y].clear();
        }
        else
		{
            f[y]+=f[x];
            f[x]=y;
            for(int j=0;j<G[x].size();j++)
                G[y].push_back(G[x][j]);
            G[x].clear();
            x=y;
        }
    }
    G[u].clear();
    G[u].push_back(x);
    dfs(x);
}
int main()
{
	memset(f,-1,sizeof(f));
	n=rd(),m=rd();
	for(int i=1;i<=m;i++)
	{
		int u=rd(),v=rd();
		G[u].push_back(v);
	}
	for(int i=1;i<=n;i++)
		dfs(i);
	int cnt=0;
	for(int i=1;i<=n;i++)
	{
		int fa=Find(i);
		if(!c[fa]) c[fa]=++cnt;
		printf("%d\n",c[fa]);
	}
	return 0;
}