帝国の狂欢（种树）（可撤销DP）

题目描述

马上就要开学了！！！

为了给回家的童鞋们接风洗尘，HZOI帝国的老大决定举办一场狂欢舞会。

然而HZOI帝国头顶上的HZ大帝国十分小气，并不愿意给同学们腾出太多的地方。所以留给同学们开party的地方只有一个教室。

这个教室里有一个长条形的舞池，这个舞池最多能让n个人同时在上面high，也就是说有n个位置，但要知道HZ大帝国对同学们间的接触限制很严（众所周知一群糙老爷们儿也是能够非正常接触的），所以实际上两个人是不可以在相邻的位置上high的。

由于不同的位置high起来的感觉不是很一样，所以每个位置都有一个high值。

但是有强迫症的老大对这个舞池设计不是很满意，于是他下令把条形的舞池改造成了圆环状，也就是说第1个位置和第n个位置现在相邻了。

所以，你的任务是计算合法安排好所有同学所能达到的最大high值和。

输入格式

输入包括两行：

第一行有两个正整数：n，m，代表舞池有n个位置，有m个童鞋要参加狂欢

第二行有n个整数：high[i]即第i个整数代表舞池第i个位置的high值

输出格式

输出共一行：

一个整数即安排好所有同学能达到的最大high值和

如果无法安排好所有的同学，则输出“High!!!”（不含引号）。

输入输出样例

输入

5 2
1 2 3 4 5

输出

8

输入

8 3
2 7 14 8 -3 0 4 9

输出

24

说明/提示

1 \(\leq\) m \(\leq\) n \(\leq\) 200000

| high[i] | \(\leq\) 2000

一点题外话

这题的根源是这儿：https://www.luogu.com.cn/problem/P1484

当时我看到这个题就寻思着要整个环，思路基本上是不变的，也算是整了个活，然后就有了这道题。然鹅后来突然发现它下面就有一道名字一毛一样的题，对没错，就是顶着国家集训队名头的那个种树……不过那题的数据范围有点尴尬，那题的很多标程的无解是直接用n<2m判过去的，数据也的确能过，但n=m=1时实际上它是有解的。这一点我开始时就被标程给带跑了，后来还是LC大锅hack了我一波（笑）。

一开始只有一个很普通的样例可能迷惑性很强，所以到一半时我又加了一个样例2，应该是能卡掉不少代码的，也不知道有人看见了没……

整个好活

题意我觉得我的语文应(shen)该(me)还(dou)可(bu)以(shi)，就不给大家复述了。

好吧还是简单说一下：就是在一个有n个点的环上取m个点，使这m个点两两不相邻，且取到的权值和最大。

可能有神犇想到用DP，但是200000的数据并不是那么友好。

这题的思路其实就是贪心，但要用到一个很巧妙很巧妙的技巧

首先最简单的贪心估计大家都能想到，那就是建一个大根堆，一个个取，每取一个把两旁相连的点都标记上不能再取。

这肯定是最原始的贪心，无论什么操作都是在这个思路之上进行的。

那么，这个思路到底哪里有毛病呢？

我们简单地模拟一下：7 14 8 0 这4个数中选两个

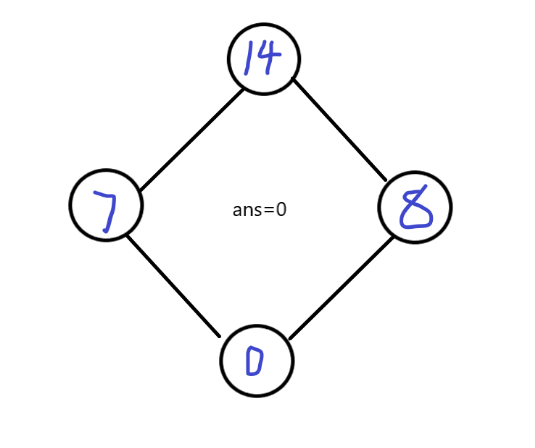
照我们刚才的思路，肯定第一步先取14，然后7跟8就标记上不能取了

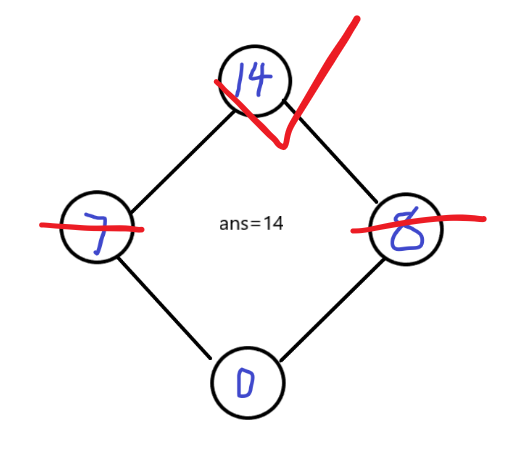
显然下一步我们能取的只有0，这样算出来最优值是14

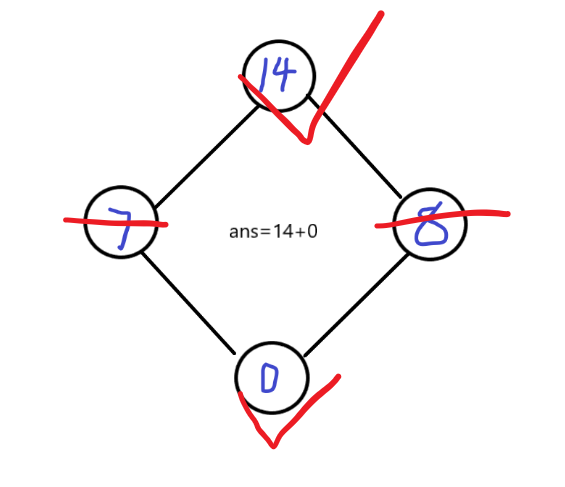
但是很显然，如果我们直接取7跟8，和是15，显然比咱们现在的14要大。

问题就出在：在点数允许的情况下，我们没有判断当前取出的这个14跟它左右相连的7跟8的和的关系，也就是说我们不能保证全局最优。

可以选择判断a[i-1].w + a[i+1].w - a[i].w与0的大小，如果大于0，我们要这两个点而不要最大的那个点。

但真正去运算时肯定不允许你这样做，我们一次这个运算只能从三个数中做一个选择，那么放到整个程序里就是从n个数中取3个数的组合数，这还是没算别的常数的说。时间显然是不允许的。

所以就要用到下面这个肥常肥常神奇的技巧：

struct node{
    int w,l,r;
}a[maxn];//存储每个节点的信息

我们简单开一个结构体，w代表当前节点的权值，l为左节点编号，r为右节点编号。

还是刚才的思路，建大根堆，每次取最大权值点，标记左右两点，但不一样的地方是：我们取完这个点后，再往根堆里插一个新的点，这个新点的权值为原来左右节点的权值和-原来该节点权值，左节点为原左节点的左节点，右节点为原右节点的右节点。

这样实际上有什么用呢？回到我们出错的原因：因为我们每次只能保证在当前情况下取最大那个数是最优的，这是贪心的基础，但我们不能保证这个选择在全局上也是最优的。所以我们需要一个保险，这个新点就是为我们提供一个后悔的选项。

我们记新点的权为 a[i-1].w + a[i+1].w - a[i].w

在当前这一步，我们选择了a[i].w，因为它最大，然后插入新点。那么，如果我们能在取到这个新点之前结束运算，那么显然选择最大的这个数就是最优选择。但如果我们一直取下去直至取到了这个新点，那么说明在刚刚的那一步中a[i].w并不是最优选择，所以我们取到了这个新点，ans就相当于在之前加上了a[i].w，然后现在又加上了a[i-1].w + a[i+1].w - a[i].w

前后合起来刚好是a[i-1].w + a[i+1].w，对于整个答案来说就相当于我们刚才那步选择了左右节点，而没有选择最大节点。

在学校里又重新听老师讲了这道题，发现有可能一个疑问就是新节点到底算几棵树的问题。有的童鞋认为算两棵，因为它不是选择了左右两棵树嘛，所以种树棵数应该++才对。但要知道我们在前面已经在最大的那个坑种树了，如果现在算两棵树，那前面那棵岂不是多了吗。所以这个新结点我们可以理解为把原来的最大坑的一棵树挪到了一边，然后在另一边种一棵新的。

综上所述，在新节点种树时并不用对棵数单独处理，直接按正常的树处理即可。

（ps：这才多长时间我就不忍看自己的代码了...码风好丑...）

#include <cstdio>
#include <queue>
#include <algorithm>
#include <cstring>
#include <iostream>
#define lson(x) a[x].l
#define rson(x) a[x].r
using namespace std;
const int maxn=200000+10;
int n,ans,m;
bool vis[maxn];
struct node{
    int w,l,r;
}a[maxn];//存储每个节点的信息
struct Node{
    int val,id;
    Node();
    Node(int x,int y){
        val=x,id=y;
    }
    bool operator <(const Node x)const{
        return val<x.val;
    }
};

priority_queue<Node> q;//大根堆

//为了方便这里直接用左右儿子来解释，实际上是左右相连的点

void Update(int x){//删去一个节点x后更新与x相关的节点
    lson(x)=a[lson(x)].l;//新点的左儿子变为原来左儿子的左儿子
    rson(x)=a[rson(x)].r;//新点的右儿子变为原来右儿子的右儿子
    a[lson(x)].r=x;
    a[rson(x)].l=x;
}
int main(){
    scanf("%d %d",&n,&m);
    int maxx=-1<<15;//可不要设成-1哦，最小值有-2000呢
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i].w);
        maxx=max(a[i].w,maxx);
        a[i].l=i-1;
        a[i].r=i+1;
        q.push(Node(a[i].w,i));
    }
    if(m==1){//特判掉n=m=1的情况
        printf("%d\n",maxx);
        return 0;
    }
    if(n<(m<<1)){//别的情况就可以直接n<2m判掉了
        printf("High!!!\n");
        return 0;
    }
    a[1].l=n,a[n].r=1;//所谓的环就只有这一步
    for(int i=1;i<=m;i++){
        while(1){
            if(vis[q.top().id]) {q.pop();continue;}//标记过的点直接pop掉
            break;
        }
        int val=q.top().val,num=q.top().id;
        q.pop();
        ans+=val;
        vis[lson(num)]=vis[rson(num)]=1;//左右相连的点标记为访问过
        a[num].w=a[lson(num)].w+a[rson(num)].w-a[num].w;//插入一个新点，新权值为原左右儿子的权值和减去原权值
        Update(num);//更新新点的左右儿子信息
        q.push(Node(a[num].w,num));
    }
    printf("%d\n",ans);
    return 0;
}