【LeetCode/LintCode】丨Google面试题：N皇后问题

n皇后问题是将n个皇后放置在n*n的棋盘上，皇后彼此之间不能相互攻击(任意两个皇后不能位于同一行，同一列，同一斜线)。

给定一个整数n，返回所有不同的n皇后问题的解决方案。

每个解决方案包含一个明确的n皇后放置布局，其中“Q”和“.”分别表示一个女王和一个空位置。

在线评测地址：

LintCode 领扣​

样例1:

输入:1
输出:
   [["Q"]]

样例2:

输入:4
输出:
[
  // Solution 1
  [".Q..",
   "...Q",
   "Q...",
   "..Q."
  ],
  // Solution 2
  ["..Q.",
   "Q...",
   "...Q",
   ".Q.."
  ]
]

算法：dfs（回溯法）

题目分析

这个问题要求把n个皇后放在一个nXn的棋盘上，使得任何两个皇后都不能相互攻击，即它们不能同行，不能同列，也不能位于同一条对角线上。对于n=1，问题的解很简单，而且很容易看出对于n=2和n=3来说，这个问题是无解的。所以我们考虑4皇后问题，并用回溯法对它求解。

算法思路

• 因为每个皇后都必须分别占据一行，我们需要做的不过是棋盘上的每个皇后分配一列。
• 下面我们用4皇后的求解过程来讲解算法思路：

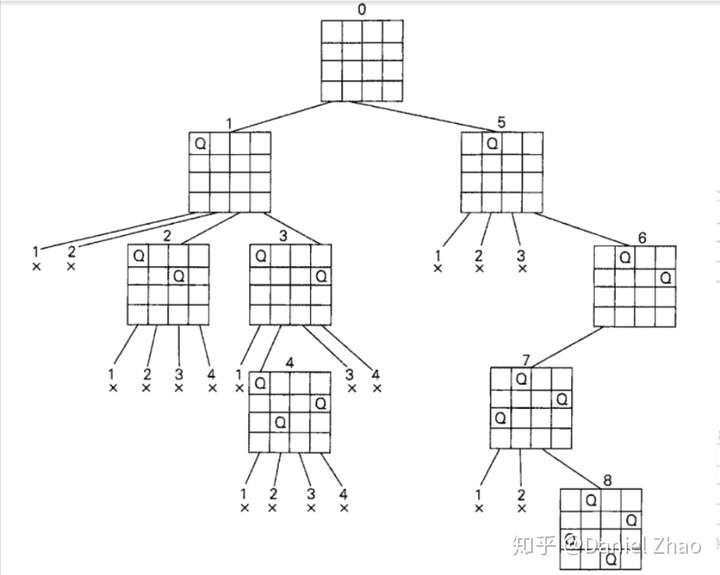
从空棋盘开始，然后把皇后1 放到它所在行的第-一个可能位置上，也就是第一-行第一列。对于皇后2，在经过第-列和第二列的失败尝试之后，我们把它放在第一个可能的位置，就是格子(2, 3)，位于第二行第三列的格子。这被证明是一个死胡同，因为皇后3将没有位置可放。所以，该算法进行回溯，把皇后2放在下一个可能位置(2,4)上。这样皇后3就可以放在(3, 2),这被证明是另一个死胡同。该算法然后就回溯到底，把皇后1移到(1,2)。 接着皇后2到(2,4)， 皇后3到(3,1)， 而皇后4到(4, 3)， 这就是该问题的一个解。

• 整个过程实际上就是一个状态树的遍历过程
• 下图为状态树

算法：dfs（回溯法）

题目分析

这个问题要求把n个皇后放在一个nXn的棋盘上，使得任何两个皇后都不能相互攻击，即它们不能同行，不能同列，也不能位于同一条对角线上。对于n=1，问题的解很简单，而且很容易看出对于n=2和n=3来说，这个问题是无解的。所以我们考虑4皇后问题，并用回溯法对它求解。

算法思路

• 因为每个皇后都必须分别占据一行，我们需要做的不过是棋盘上的每个皇后分配一列。
• 下面我们用4皇后的求解过程来讲解算法思路：

从空棋盘开始，然后把皇后1 放到它所在行的第-一个可能位置上，也就是第一-行第一列。对于皇后2，在经过第-列和第二列的失败尝试之后，我们把它放在第一个可能的位置，就是格子(2, 3)，位于第二行第三列的格子。这被证明是一个死胡同，因为皇后3将没有位置可放。所以，该算法进行回溯，把皇后2放在下一个可能位置(2,4)上。这样皇后3就可以放在(3, 2),这被证明是另一个死胡同。该算法然后就回溯到底，把皇后1移到(1,2)。 接着皇后2到(2,4)， 皇后3到(3,1)， 而皇后4到(4, 3)， 这就是该问题的一个解。

• 整个过程实际上就是一个状态树的遍历过程
• 下图为状态树

代码思路

• 按行摆放，在确定一个皇后应该摆的列时，需要检查当前列是否合法，如果合法，则将皇后放置在当前位置，并进行递归，回溯。每行都摆满皇后时，则产生了一种解法，将所有解法收集并返回。
• 合法性判断方法：当前将要摆放皇后的位置和其他已摆放皇后的位置不能在同一列，且不能在同一条斜线上。这里判断是否在同一条斜线上可以通过两个皇后的位置横坐标之差和纵坐标之差的绝对值是否相等来判断。

复杂度分析

• 空间复杂度：O(N!)
• 时间复杂度：O(N!)
• 放置第一个皇后有 N 种可能，放置两个皇后不超过N(N-2)种可能，放置三个皇后不超过N(N - 2)(N - 4)种可能 ，以此类推。

class Solution {
    /**
     * Get all distinct N-Queen solutions
     * @param n: The number of queens
     * @return: All distinct solutions
     * For example, A string '...Q' shows a queen on forth position
     */
    List<List<String>> solveNQueens(int n) {
        // result用于存储答案
        List<List<String>> results = new ArrayList<>();
        if (n <= 0) {
            return results;
        }
        search(results, new ArrayList<Integer>(), n);
        return results;
    }
    // search函数为搜索函数，n表示已经放置了n个皇后，cols 表示每个皇后所在的列
    private void search(List<List<String>> results, List<Integer> cols, int n) {
        // 若已经放置了n个皇后表示出现了一种解法，绘制后加入答案result
        if (cols.size() == n) {
            results.add(Draw(cols));
            return;
        }
        // 枚举当前皇后放置的列，若不合法则跳过
        for (int colIndex = 0; colIndex < n; colIndex++) {
            if (!isValid(cols, colIndex)) {
                continue;
            }
            // 若合法则递归枚举下一行的皇后
            cols.add(colIndex);
            search(results, cols, n);
            cols.remove(cols.size() - 1);
        }
    }
    // isValid函数为合法性判断函数
    private boolean isValid(List<Integer> cols, int col) {
        int row = cols.size();
        for (int rowIndex = 0; rowIndex < cols.size(); rowIndex++) {
            //若有其他皇后在同一列或同一斜线上则不合法
            if (cols.get(rowIndex) == col) {
                return false;
            }
            if (row + col == rowIndex + cols.get(rowIndex)) {
                return false;
            }
            if (row - col == rowIndex - cols.get(rowIndex)) {
                return false;
            }
        }
        return true;
    }
    // Draw函数为将 cols 数组转换为答案的绘制函数
    private List<String> Draw(List<Integer> cols) {
        List<String> result = new ArrayList<>();
        for (int i = 0; i < cols.size(); i++) {
            StringBuilder sb = new StringBuilder();
            for (int j = 0; j < cols.size(); j++) {
                sb.append(j == cols.get(i) ? 'Q' : '.');
            }
            result.add(sb.toString());
        }
        return result;
    }
}

更多题解参考：

九章算法 - 帮助更多中国人找到好工作，硅谷顶尖IT企业工程师实时在线授课为你传授面试技巧​