洛谷 P5022 旅行

今天换标题格式了，因为感觉原版实在有点别扭……

还是直接上题板，看完题再讲吧：

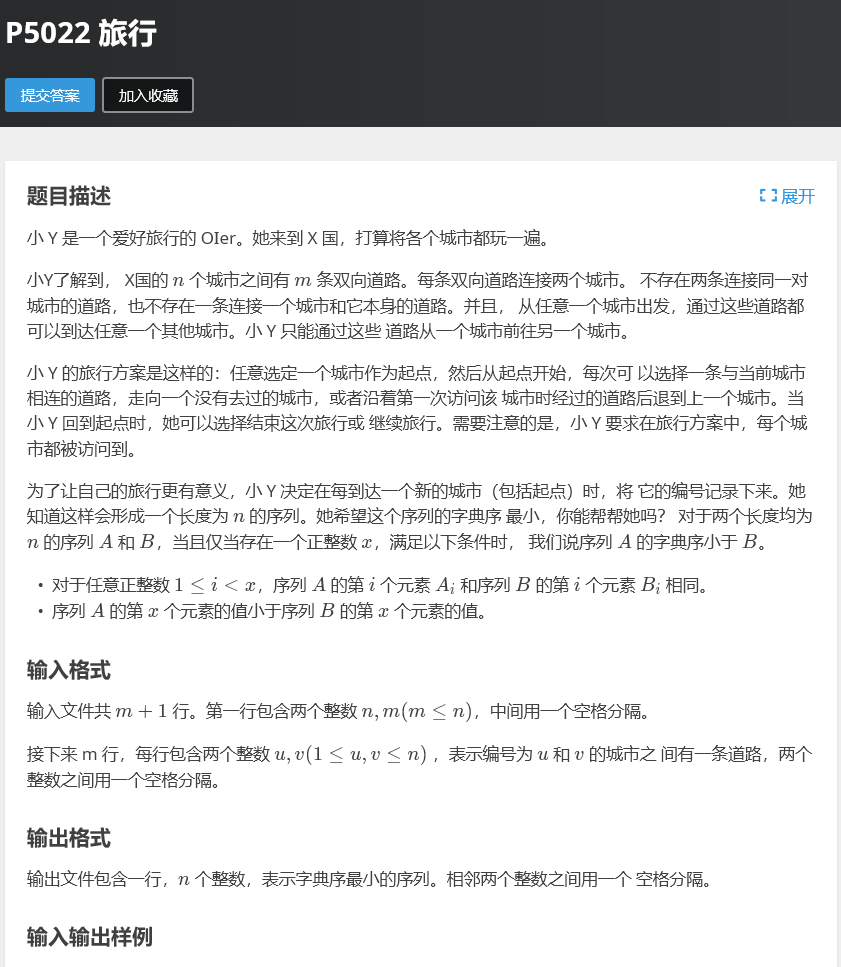
对了有个小细节没说，m一定是等于n或者等于n-1的。

这题是2018年提高组的真题哦！被我肝了2天肝出来了，2天……（真打提高怕不是废了）

哎呀不说废话直接开始。首先我们知道m肯定等于n或者n-1，就可以把这个题分成2种情况：

先做第一种：好做的m等于n-1

在m等于n-1的情况，是不存在指针在里面转圈圈，转到一半还要退出来的情况的。至于这是为什么，我们可以把他看成是一个每个点的入度都为一的图，每个点只有一次从别的点来这个点（不算从别的点退回来）的机会（虽然有些数据看上去不是这样，但其实就是这样），所以我们只要先把输入点按从小到大排个序，然后用小猪佩奇和大家都喜欢用的邻接表存图，再把图遍历一遍就ok了。（起点肯定是1，字典序最小的序列一定是1开头的）

然后再做第二种：难做的m等于n

这种我用了链式前向星的哟~

什么？你说你不会链式前向星？想学习一下吗，请戳这里。

这一定不是我给自己打广告(大声bb)

在m等于n的情况下，一些邪恶的数据会让你在里面转圈圈，然后他的正解还是转到一半就停下。哎呀呀怎么办呢？我又不会高端算法……但我的老师告诉我，暴力出奇迹，偏分过样例。

但是做题得不了满分，你的程序还有什么用呢？我就算不做，noip提高爆零，也绝不会暴力的！

然后我就开始打模拟了（嗯真香），愉快的得了85分。然后我因为不会做看着题目发呆……（同学们别学我）然后我阴差阳错的又看了一遍数据表：

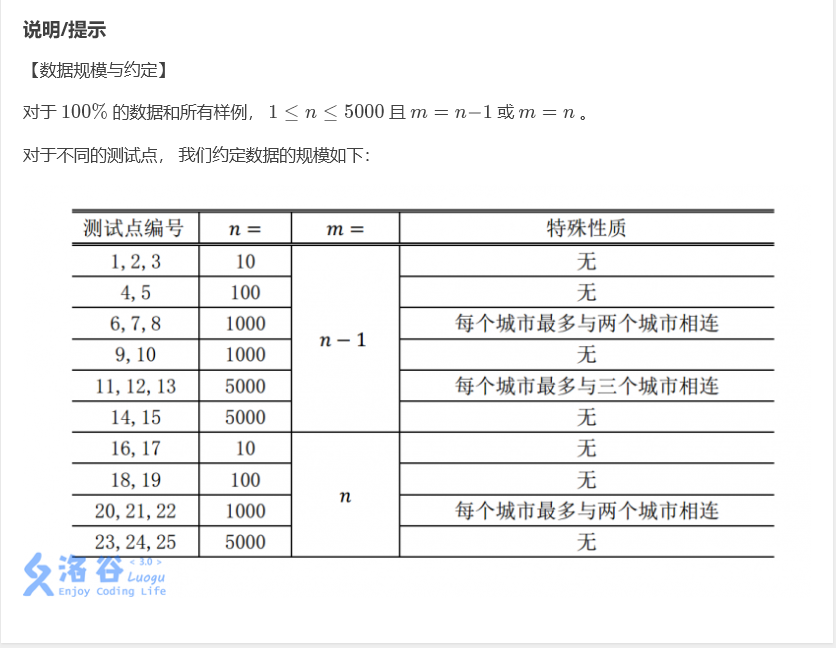
哎我的程序应该效率是O(n^2)多一点。n^2应该是25000000，应该里AC只差一点点了，只要加一点适度的优化。于是我重新审视了我的代码。

我之前的代码是纯洁的暴力，虽然道路有m条，但我们只需要m-1条，所以我们就暴力去掉一条没用的吧！真是个好主意！

然后暴力去掉一条没用的之后就开始纯洁暴力……现在就相当于m等于n-1的局势了，所以现在的操作和第一种一样，把图遍历一遍就ok了。

怎么样，是不是看起来没啥毛病（然鹅大佬早就看出了瑕疵）

桥豆麻袋，别急着提交，搜索里有个神奇的东西叫做最优化剪枝。

也就是说，如果我们之前找到了一个比这个方法更优的方法，那这个就完全没必要再试了！然后我们只要在每一位存进数组的时候检查一下是否符合要求，符合就加入，不符合直接丢掉……

就可以剩下很多时间啊！（这么好想我竟然没想到……而且还因为大小于号打反调试了2小时，zz体制再次实锤……）

于是我们A了。

好了好了，接下来就是代码讲解时间：

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;
long long t,w,ans,head[5005],zshu[5005],za[5005],ja,jb,zac;//head数组是链式前向星要用的，head[i]用来标记最后一个出发点为i的位置。 za是用来暂存新方案的数组
long long n,m;//想必不用解释
long long a,b;
long long zy[5005];//zy是最优方案。
long long fh=0;
struct hehe
{
	long long t,w,syg;//t是头，w是尾，syg是上一个头为t的编号。（写完才发现t毛用没有）
}lsqxx[10005];//lsqxx，链式前向星的首字母
void add(long long t,long long w)
{
	ans++;
	lsqxx[ans].t=t;//这句话完全可以删掉
	lsqxx[ans].w=w;
	lsqxx[ans].syg=head[t];//这个的意思是保存上一个为t的编号。
	head[t]=ans;//现在他自己就是上一个。
}
vector<long long>sz[5005];//排序用的（vector是真的香）
long long zhi,bj[5005];//bj是不要走回头路的标记
int px(long long a1,long long a2)
{
	return a1<a2;//排序方法，学过sort的都知道
}
void dfs(long long z,long long f)//这里就是计算m等于n-1的情况的函数
{
	if(bj[z]==1)//可行性剪枝
	{
		return;
	}
	bj[z]=1;
	printf("%lld ",z);//肯定最小的。为什么？因为前面排过序了。
	for(int i=0;i<sz[z].size();i++)
	{
		zhi=sz[z][i];
		if(zhi==f)//继续可行性
		{
			continue;
		}
		dfs(zhi,z);//选定地点，继续出发
	}
}
void dfs2(long long z,long long f)//这个就是m等于n的时候的函数
{
	if(bj[z]==1)//随处可见的可行性剪枝
	{
		return;
	}
	bj[z]=1;
	za[zac]=z;//候选新成员
	if(za[zac]<zy[zac])//这个比之前的都小，就算以后再大，这个也是目前字典序最小的
	{
		fh=1;
	}else if(za[zac]>zy[zac])//这个爆掉了~
	{
		if(fh==0)//彻底爆掉了~
		{
			return;
		}
	}
	zac++;//下一个位置
	for(int i=0;i<sz[z].size();i++)
	{
		zhi=sz[z][i];
		if(zhi==f)
		{
			continue;
		}
		if((zhi==ja&&z==jb)||(zhi==jb&&z==ja))//ja和jb就是被禁止通行的2个端点编号
		{
			continue;
		}
		dfs2(zhi,z);
	}
}
void zhuanyi()
{
	for(int i=0;i<=n-1;i++)//最小序列,易主。
	{
		zy[i]=za[i];
	}
}
int main()
{
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=m;i++)
	{
		scanf("%lld%lld",&a,&b);
		sz[a].push_back(b);//在可通行列表里加上
		sz[b].push_back(a);
		add(a,b);
		add(b,a);
	}
	for(int i=1;i<=n;i++)
	{
		sort(sz[i].begin(),sz[i].end(),px);//排序
	}
	if(m==n-1)
	{
		dfs(1,2147483647);//第一种情况，直接开始
		return 0;
	}else//恶心的第二种情况
	{
		for(int i=0;i<=n;i++)//开局重置（不知道为什么，用memset会爆掉，可能他不让设定太大的初始值）
		{
			zy[i]=2147483647;
		}
		for(int i=1;i<=ans;i+=2)//链式前向星的威力出现了（感觉好没用）
		{
			zac=0;//防止去掉了一个必须要经过的道路（就是长度不够）
			fh=0;//这个是通过与否的标记
			ja=lsqxx[i].t;//顶下2个不能互通的顶点
			jb=lsqxx[i].w;//同上
			memset(bj,0,sizeof(bj));//bj数组初始化
			dfs2(1,2147483647);//开始尝试
			if(zac<n)//emm失误了。
			{
				continue;
			}
			if(fh==1)//这个序列字典序比之前都小。
			{
				zhuanyi();//转移
			}
		}
		for(int i=0;i<=n-1;i++)//字典序最小序列出炉
		{
			printf("%lld ",zy[i]);
		}
	}
	return 0;
}

懒得讲解所以我就写成注释了

好了这篇博客就到这里。

对了这个代码只能过普通版，数据加强版是过不了的，各位渴望知识的同学们还是找别的大佬吧（大声的忠告）