DES加密详解

目录

• 1 根据输入的秘钥得到16个子秘钥
  • 1.1 大致流程
  • 1.2 利用PC-1从K_0中挑出K_1
  • 1.3 利用PC-2从K_1中挑出16个子秘钥
• 2 利用16个子秘钥对明文进行加密
  • 2.1 大致流程
  • 2.2 将R_0扩展成48位的二进制串, 并与子秘钥k模二加
  • 2.3 使用S1-S8表将48位变回32位
  • 2.4 使用P表对32位输出进行位置变换, 并和L0相加
  • 2.5 往复这样的步骤16次, 将得到的R_16和L_16拼接并经IP^-1变换
• 3 代码实现

注: 下述所有加法均为模二加, 即为亦或运算

1 根据输入的秘钥得到16个子秘钥

1.1 大致流程

graph TB;
a[输入一个64位长度的字符串,即为秘钥K_0]
b[根据PC-1表挑出56位作为新秘钥K_1]
c[K_1拆分,循环左移得到16个子秘钥k0...k15]
d[使用PC-2表从各子秘钥56位中挑出48位]

a-->b-->c-->d

图1.1.1 算法流程

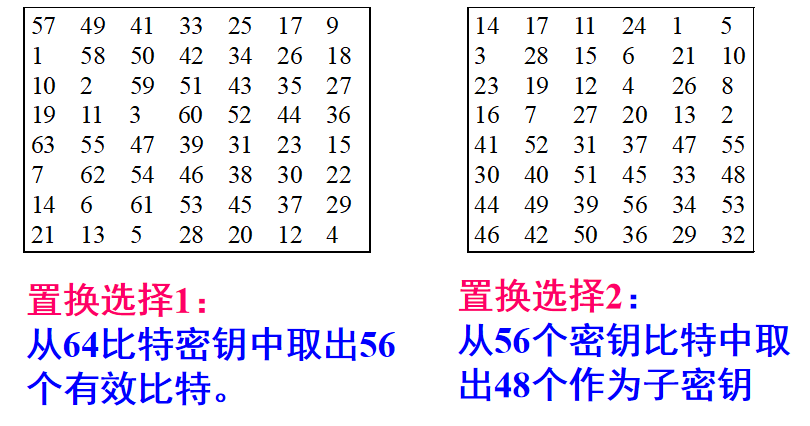
图1.1.2 PC-1表及PC-2表

1.2 利用PC-1从K_0中挑出K_1

​ 接下来我们以输入的秘钥为"0x123456789abcdeff"为例, 及二进制编码为:

"0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 1111"

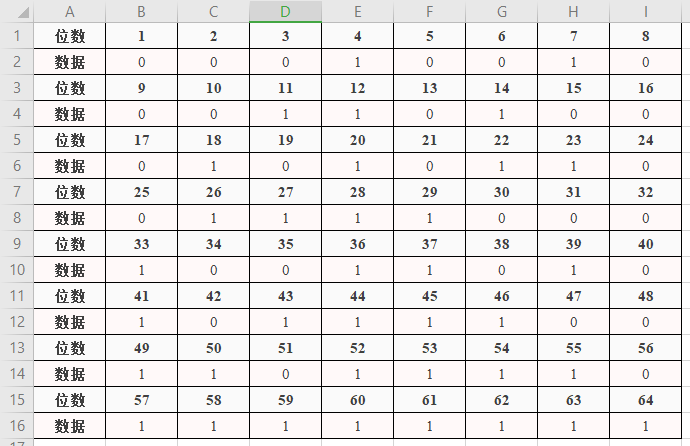
图1.2.1 初始秘钥K_0

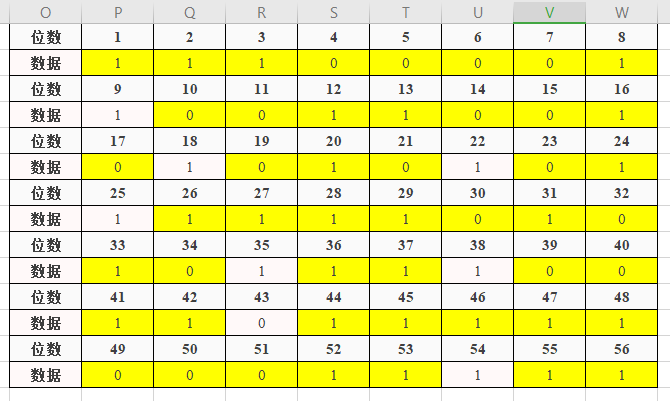
​ 接下来我们利用PC-1表生成新秘钥K_1

图1.2.2 挑出的56位二进制串

"1111 0000 1100 1100 1010 1010 1111"和"1101 0101 1110 0110 1111 1000 1111"

两边各是28位, 共56位

1.3 利用PC-2从K_1中挑出16个子秘钥

​ 对于从1.2得来的一串56位二进制码, 我们将其拆分成两串28位二进制码, 即为:

左半部分的"1111 0000 1100 1100 1010 1010 1111", 并将其命名为C_0

右半部分的"1101 0101 1110 0110 1111 1000 1111", 并将其命名为D_0

​ 接下来, 我们利用下表, 进行循环左移, 规则如下:

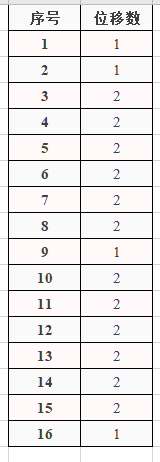
图1.3.1 位移规则表

​ 之后我们按照上面的规则, 展示子秘钥k_1是如何生成的:

1. 将C_0和D_0分别循环左移1位, 得到C_1-"1110 0001 1001 1001 0101 0101 1111"以及D_1-"1010 1011 1100 1101 1111 0001 1111"(PS:循环左移1位就是将首位移动到最后末尾)
2. 将C_1即D_1拼接起来, 得到"1110 0001 1001 1001 0101 0101 1111 1010 1011 1100 1101 1111 0001 1111"
3. 利用PC-2表从拼接得到的字符串中挑选出子秘钥k_1, 类似于"利用PC-1表的过程"

图1.3.2 从C_0和D_0中生成的子秘钥k_0

1. 所以子秘钥k_1为"0001 1011 0000 0010 1110 1111 1111 1100 0111 1001 0111 0110"

​ 按照同样的逻辑, 在C_0和D_0已被循环左移的基础上, 重复上述步骤, 我们得到如下16个子秘钥:

图1.3.3 生成的所有子秘钥

​ PS: 上述输出为自己写的代码, 在文末会进行展示.

​ 得到了这16个子秘钥后, 我们就可以对明文进行加密了, 我们继续!

2 利用16个子秘钥对明文进行加密

2.1 大致流程

graph TB;
a[对64位的明文进行初始变化,简称IP-Initial Permutation]
b[将IP后的明文平分成32位的L0-左半边和R0-右半边]
c[接下来使用如下公式对L_n和R_n进行变换]
d["1.L_n=R_n-1<br>2.R_n=L_n-1 + f(R_n-1, k_n)"]
e["f的具体过程如下<br>1.将R_n-1扩展成48位并与k_n-1相加"得到S盒<br>2.使用8张S表将48位的S盒运算成32位输出P<br>3.使用P表对输出P进行位置变换]
f["得到输出L_16和R_16, 拼接成R_16L_16的64位输出"]
g["对这64位输出使用IP-1表进行位置变换, 即得到最终输出"]
a-->b-->c-->d-.-e-.->f-->g
d--重复16次-->d

图2.1.1 算法流程

2.2 将R_0扩展成48位的二进制串, 并与子秘钥k模二加

​ 我们以输入的明文为"0x0123456789abcdef"为例, 即二进制编码为:

"0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111"

经过变换后,得到:

"1100 1100 0000 0000 1100 1100 1111 1111 1111 0000 1010 1110 1111 0000 1010 1010"

将其拆分为L_0及R_0, 各32位

L_0: "1100 1100 0000 0000 1100 1100 1111 1111"

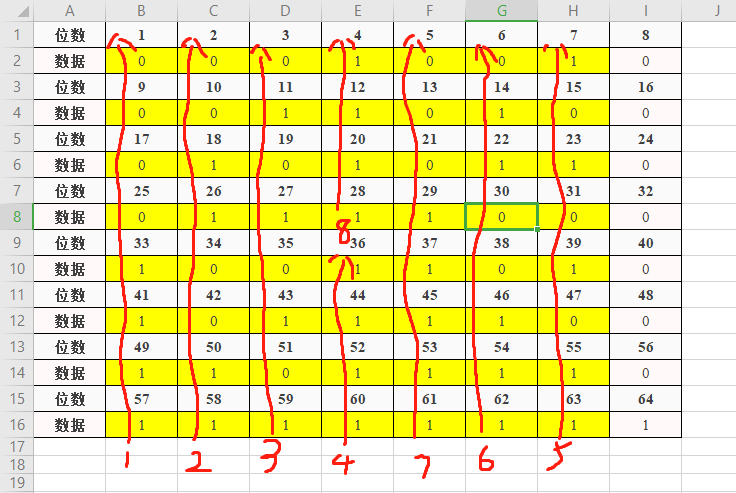
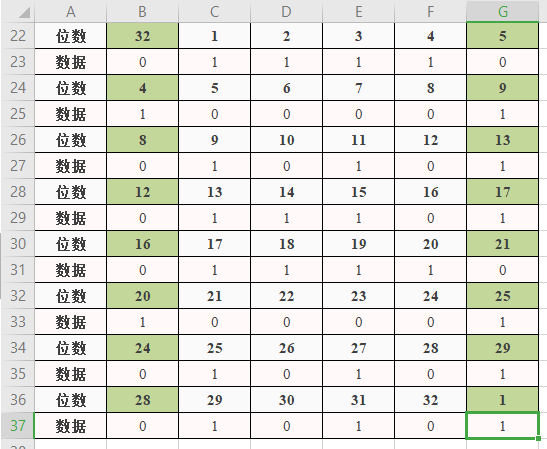
R_0: "1111 0000 1010 1110 1111 0000 1010 1010"

对R_0使用如下规则扩展成48位:

图2.2.1 R_0扩展成48位规则

PS: 绿色的标出的位数即为扩展出的12位

因此, 得到RExtend(8个6位): "011110 100001 010101 011101 011110 100001 010101 010101"

将其与子秘钥"0001 1011 0000 0010 1110 1111 1111 1100 0111 1001 0111 0110"

亦或得S盒"0110 0001 0001 0111 1011 0010 1000 0110 0110 1100 0010 0011"

2.3 使用S1-S8表将48位变回32位

​ 为什么上面S盒要备注8个6位呢? 原因就是要以8个6位为输入, 分别经过S1-S8盒的运算,得到8个4位输出, 也就变成了32位.

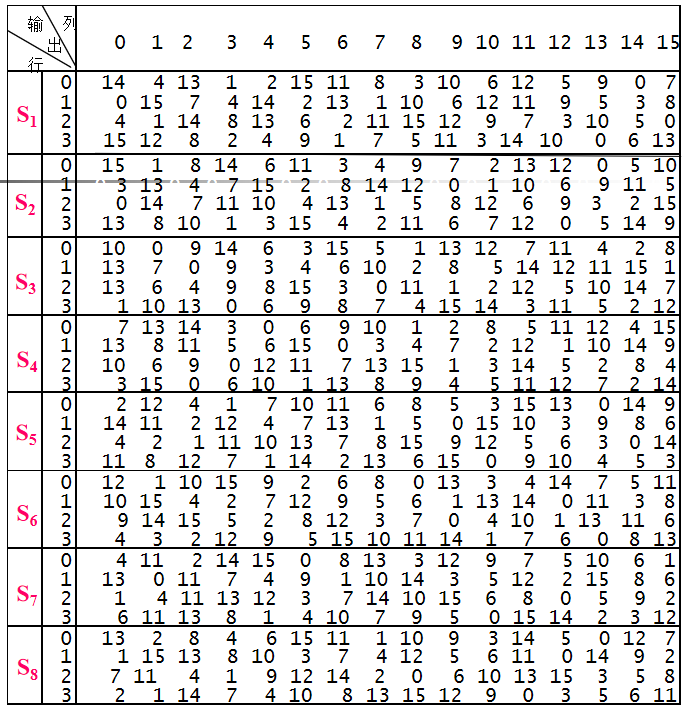
图2.3.1 S1-S8表

我们的S盒长这样"011000 010001 011110 110010 100001 100110 110000 100011"

以第一个6位"011000"为输入, 代入到S1表变换

以"011000"的首位和末尾拼起来的数字为行号, 中间4位为列号(当然都是二进制的), 即第0(00b)行, 第15(1100b)列, 查询S1表, 为S1(0, 12) = 5 = 0101b

这样就可以得到第一个4位的输出, 按照这样的方式可以得到8个4位的输出, 合在一起就是一个32位的输出, 经过运算是"0101 1100 1000 0001 1011 0101 1010 0001"

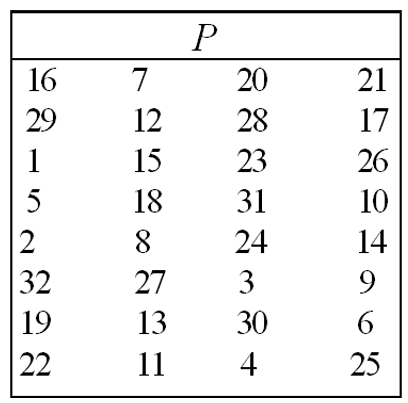
2.4 使用P表对32位输出进行位置变换, 并和L0相加

​ 我们已经得到经过"扩位"和"缩位"的变换, 现在要按照P表进行简单的位置变换:

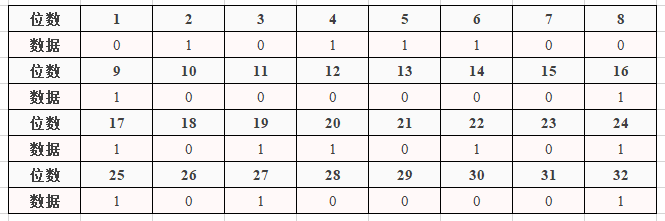
图2.4.1 P表

图2.4.2 32位输出的每一位情况

照着P表生成新的32位输出"1010 0001 0000 1000 1010 1101 1001 1011"

再将输出与L_0相加, L_0:"1100 1100 0000 0000 1100 1100 1111 1111"

得到结果: "0110 1101 0000 1000 0110 0001 0110 0100"

2.5 往复这样的步骤16次, 将得到的R_16和L_16拼接并经IP^-1变换

​ 如题, 得到最终结果:

"1110 1100 1010 1001 0011 1101 1001 1100 1110 0100 1101 1001 1001 1001 1100 1110"

3 代码实现

/*
 * @Description:
 * @Autor: Shmily
 * @Date: 2021-03-01 23:40:00
 * @LastEditTime: 2021-03-02 22:35:49
 */

#include <bits/stdc++.h>
using namespace std;

const int8_t PC_1[56] = {
  57, 49, 41, 33, 25, 17, 9, 1,
  58, 50, 42, 34, 26, 18, 10, 2,
  59, 51, 43, 35, 28, 19, 11, 3,
  60, 52, 44, 36,
  63, 55, 47, 39, 31, 23, 15, 7,
  62, 54, 46, 38, 30, 22, 14, 6,
  61, 53, 45, 37, 29, 21, 13, 5,
  28, 20, 12, 4
};

const int8_t PC_2[48] = {
  14, 17, 11, 24, 1, 5,
  3, 28, 15, 6, 21, 10,
  23, 19, 12, 4, 26, 8,
  16, 7, 27, 20, 13, 2,
  41, 52, 31, 37, 47, 55,
  30, 40, 51, 45, 33, 48,
  44, 49, 39, 56, 34, 53,
  46, 42, 50, 36, 29, 32
};

const int8_t left_move[16] = {
  1, 1, 2, 2, 2, 2, 2, 2,
  1, 2, 2, 2, 2, 2, 2, 1
};

const int8_t S8[8][4][16] = {
  // S1
  {
    {14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7},
    {0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8},
    {4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0},
    {15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13}
  },
  // S2
  {
    {15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10},
    {3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5},
    {0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15},
    {13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9}
  },
  // S3
  {
    {10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8},
    {13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1},
    {13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7},
    {1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12}
  },
  // S4
  {
    {7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15},
    {13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9},
    {10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4},
    {3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14}
  },
  // S5
  {
    {2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9},
    {14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6},
    {4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14},
    {11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3}
  },
  // S6
  {
    {12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11},
    {10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8},
    {9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6},
    {4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13}
  },
  // S7
  {
    {4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1},
    {13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6},
    {1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2},
    {6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12}
  },
  // S8
  {
    {13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7},
    {1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2},
    {7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8},
    {2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11}
  }
};

const int8_t PTable[32] = {
  16, 7, 20, 21,
  29, 12, 28, 17,
  1, 15, 23, 26,
  5, 18, 31, 10,
  2, 8, 24, 14,
  32, 27, 3, 9,
  19, 13, 30, 4,
  22, 11, 4, 25
};

const int8_t IP[2][64] = {
  {
    58, 50, 42, 34, 26, 18, 10, 2,
    60, 52, 44, 36, 28, 20, 12, 4,
    62, 54, 46, 38, 30, 22, 14, 6,
    64, 56, 48, 40, 32, 24, 16, 8,
    57, 49, 41, 33, 25, 17, 9, 1,
    59, 51, 43, 35, 27, 16, 11, 3,
    61, 53, 45, 37, 29, 21, 13, 5,
    63, 55, 47, 39, 31, 23, 15, 7
  },
  {
    40, 8, 48, 16, 56, 24, 64, 32,
    39, 7, 47, 15, 55, 23, 63, 31,
    38, 6, 46, 14, 54, 22, 62, 30,
    37, 5, 45, 13, 53, 21, 61, 29,
    36, 4, 44, 12, 52, 20, 60, 28,
    35, 3, 43, 11, 51, 19, 59, 27,
    34, 2, 42, 10, 50, 18, 58, 26,
    33, 1, 41, 9, 49, 17, 57, 25
  }
};

void out_int8_t(int8_t* out, int len) {
  for (int i = 0; i < len; i++) {
    printf("%d", out[i]);
    if ((i + 1) % 4 == 0) cout << " ";
  }
  cout << endl;
}

void fun_left_move(int8_t* C_0, int8_t* D_0, int times_left) {
  for (int i = 0; i < times_left; i++) {
    int8_t temp1 = C_0[0];
    int8_t temp2 = D_0[0];
    for (int j = 1; j < 28; j++) {
      C_0[j - 1] = C_0[j];
      D_0[j - 1] = D_0[j];
    }
    C_0[27] = temp1;
    D_0[27] = temp2;
  }
}

void Extend32To48(int8_t (*R) [32], int8_t (*RExtend) [48], int times) {
  RExtend[times][0] = R[times][31];
  RExtend[times][47] = R[times][0];
  for (int i = 1; i < 47; i++) {
    // 6个位一组, 即为一行
    int LineNumber = (int)(i / 6);
    RExtend[times][i] = R[times][i - 1 - LineNumber*2];
  }
}

void XOR(int8_t (*RExtend) [48], int8_t (*k) [48], int8_t (*S) [48], int times) {
  for (int i = 0; i < 48; i++) {
    // 进行模二加运算
    S[times][i] = (RExtend[times][i] + k[times][i]) % 2;
  }
}

void XOR(int8_t (*L) [32], int8_t (*Pchanged) [32], int8_t (*R) [32], int times) {
  for (int i = 0; i < 32; i++) {
    R[times + 1][i] = (L[times][i] + Pchanged[times][i]) % 2;
  }
}

void UseS48To32(int8_t (*S) [48], int8_t (*P) [32], int times) {
  for (int i = 0; i < 8; i++) {
    int line = 0, row = 0;
    // 计算出行号及列号
    line = line + S[times][i*6]*2 + S[times][5 + i*6];
    row = row + S[times][1 + i*6]*8 + S[times][2 + i*6]*4 + S[times][3 + i*6]*2 + S[times][4 + i*6];
    // 从S表中挑出答案
    int8_t ans = S8[i][line][row];
    for (int j = 0; j < 4; j++) {
      int subtrahend = pow(2, (3 - j));
      if (ans - subtrahend >= 0) {
        P[times][j + i*4] = 1;
        ans -= subtrahend;
      }
      else P[times][j + i*4] = 0;
    }
  }
}

void UsePChangeP(int8_t (*P) [32], int8_t (*PChanged) [32], int times) {
  for (int i = 0; i < 32; i++) {
    PChanged[times][i] = P[times][PTable[i] - 1];
  }
}

void UseIPChange(int8_t* in, int8_t* out, int8_t choice) {
  for (int i = 0; i < 64; i++) {
    out[i] = in[IP[choice][i] - 1];
  }
}

int main(void) {
  // 对秘钥进行处理
  // 输入为64位秘钥， 输出位16个32位子秘钥
  int8_t K_0[64], K_1[56], k[16][48];
  // 秘钥为"0x123456789abcdeff"
  char in[] = "0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 1111";
  int len = strlen(in);
  // 将输入的秘钥存储到K_0中
  for (int i = 0, j = 0; i < len; i++) {
    if (in[i] == '0') K_0[j++] = 0;
    else if (in[i] == '1') K_0[j++] = 1;
  }
  // 利用PC-0表, 从K_0中取出K_1
  for (int i = 0; i < 56; i++) {
    // 注意-1
    K_1[i] = K_0[PC_1[i]-1];
  }
  // 上述完成了第一步利用PC-1表
  // 接下来利用PC-2表
  int8_t C_0[28], D_0[28];
  // 将K_1拆分
  for (int i = 0; i < 56; i++) {
    if (i < 28) C_0[i] = K_1[i];
    else D_0[i - 28] = K_1[i];
  }
  // 循环16次生成16个子秘钥
  for (int i = 0; i < 16; i++) {
    int8_t times_left = left_move[i];
    fun_left_move(C_0, D_0, times_left);
    for (int j = 0; j < 48; j++) {
      int8_t sub = PC_2[j] - 1;
      if (sub < 28) k[i][j] = C_0[sub];
      else k[i][j] = D_0[sub - 28];
    }
    // printf("子秘钥k[%.2d]: ", i + 1);
    // out_int8_t(k[i], 48);
  }

  // 对明文进行处理
  // 明文为"0x0123456789abcdef"
  char in_text[] = "0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111";
  int8_t PlainText[64], IP_PlainText[64], EnchiperTextInitial[64], EnchiperText[64];
  int8_t L[17][32], R[17][32], RExtend[16][48], S[16][48], P[16][32], PChanged[16][32];
  int len_text = strlen(in_text);
  // 64位明文存储到PlainText中
  for (int i = 0, j = 0; i < len; i++) {
    if (in_text[i] == '0') PlainText[j++] = 0;
    else if (in_text[i] == '1') PlainText[j++] = 1;
  }
  // 使用IP对PlainText进行变换
  UseIPChange(PlainText, IP_PlainText, 0);
  // 将PlainText分左右存储到L_0及R_0中
  for (int i = 0; i < 64; i++) {
    if (i < 32) L[0][i] = IP_PlainText[i];
    else R[0][i - 32] = IP_PlainText[i];
  }
  // 循环16次
  for (int times = 0; times < 16; times++) {
    // L_n = R_n-1
    for (int i = 0; i < 32; i++) {
      L[times + 1][i] = R[times][i];
    }

    // L_n = L_n-1 + f(R_n-1, k_n)
    // 对R进行扩展
    Extend32To48(R, RExtend, times);

    // 将RExtend与k_n-1模二加
    XOR(RExtend, k, S, times);

    // 使用S表将S盒48位压缩成32位
    UseS48To32(S, P, times);

    // 使用P表对P进行位置变换
    UsePChangeP(P, PChanged, times);

    // 生成的PChanged就是经过f之后的
    // 模二加后放入R_n
    XOR(L, PChanged, R, times);
  }

  for (int i = 0; i < 64; i++) {
    if (i < 32) EnchiperTextInitial[i] = R[16][i];
    else EnchiperTextInitial[i] = L[16][i - 32];
  }
  // 使用IP^-1对EnchiperTextInitial的进行变换得到Enchiper
  UseIPChange(EnchiperTextInitial, EnchiperText, 1);

  //最终结果输出
  out_int8_t(EnchiperText, 64);

  return 0;
}