woj1016 cherry blossom woj1017 Billiard ball 几何

---

title: woj1016 cherry blossom

date: 2020-03-18 20:00:00

categories: acm

tags: [acm,几何,woj]

几何题，判断给出的点是否对称

1 题目描述

March is wonderful in Wuhan University for the blooming cherry blossoms. Walking in the campus, you can smell the fragrance and feel the

romance with the tardiness falling of cherry blossom petals, and after a while you will see the ground will be covered by the beautiful

blossom petals.

Now, here comes the problem: the figure shown below is the cherry blossom petals on the ground, where the black points stand for blossom

petals. And this figure on the left is up-down symmetric as it is possible to cut the figure into two identical halves by the dashed line

shown in it, but the figure on the right is not.

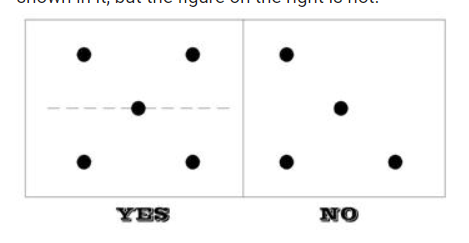
This figure shows the sample input data

Given such a figure, can you tell me whether it is up-down symmetric or not. All the black points are different from each other.

2 输入输出

输入格式

There are multiple test cases.For each test case, it contains:

Line 1: One integer N (1<=N<=1000) which specifies the number of the cherry blossom petals in this test case.

Line 2?N+1: Two integers X and Y (you are ensured that the absolute value of both the integers are less than) which specify the position of the

cherry blossom petal.

Input will be terminated by EndOfFile.

输出格式

Print exactly one line for each test case. You should output YES if the figure is up-down symmetric, else output NO.

3 样例

样例输入

5

0 0

2 0

1 1

0 2

2 2

4

0 0

2 0

1 1

0 2

样例输出

YES

NO

4 分析

//题意 输入樱花坐标，判断所有点是否上下对称。

//因为数量小所以可以直接存图 1000

//思路：找到纵坐标最低最高点,得到对称轴高度，然后判断每个x坐标上的点是否符合在对称轴两侧

//输入的时候做处理，使得所有的x坐标相同的点都放到一个vector数组，然后排序，那么对应的i,len-i两个点如果不对称，就不对称了。

//注意某个x坐标奇数个点有一个点应该在对称轴上

5 code

#include<iostream>
#include<vector>
#include<algorithm>
#include<map>
#include<cmath>
using namespace std;

const double eps=1e-6;

vector<int>xcoor;
vector<int>ycoor[1005];
int a,b,num,len,maxh,minh;
double avg;
vector<int>::iterator iter;
bool flag;
int main(){
    while(cin>>num){
        flag=true;
        xcoor.clear();
        for(int i=0;i<num;i++)
            ycoor[i].clear();
        cin>>a>>b;
        minh=maxh=b;
        xcoor.push_back(a);
        ycoor[xcoor.size()-1].push_back(b);
        for(int i=1;i<num;i++){
            cin>>a>>b;
            minh=minh>b?b:minh;
            maxh=maxh>b?maxh:b;
            if((iter=find(xcoor.begin(),xcoor.end(),a))!=xcoor.end()){
                ycoor[iter-xcoor.begin()].push_back(b);
            }
            else{
                xcoor.push_back(a);
                ycoor[xcoor.size()-1].push_back(b);
            }
        }
        avg=((double)minh+maxh)/2;         //注意double
        for(int i=0;i<xcoor.size();i++){
                len=ycoor[i].size();
                sort(ycoor[i].begin(),ycoor[i].end());
                for(int j=0;j<len/2;j++)
                    if(fabs(ycoor[i][j]+ycoor[i][len-j-1]-2*avg-0)>eps) //两边的点是否对称
                        {flag=false;break;}
                if(len&1==1){                          //一开始写成^1了....
                    if(fabs(avg-ycoor[i][len/2])>eps) //中间点是否在对称轴上
                        flag=false;
                }
                if(flag==false)
                    break;
        }
        if(flag)
            cout<<"YES"<<endl;
        else
            cout<<"NO"<<endl;
    }
    return 0;
}

---

title: woj1017 Billiard ball 几何

date: 2020-03-18 21:43:00

categories: acm

tags: [acm,woj,几何,数学]

一道三角几何题，用到余弦定理，圆周角定理，画图...

1 描述

There is a billiard table with acute triangle shape, and there are pockets at the three corners. A billiard ball hits the side of the table not at a

corner, it is reflected in the mirror direction. And it continues to travel on the table and we assume that the energy of this ball will not be

consumed, so the velocity of the ball is a constant number in the running process.

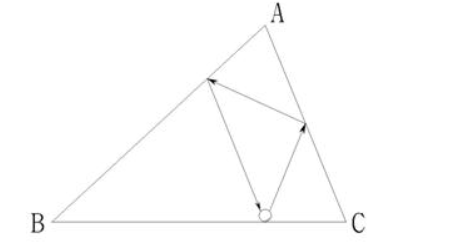
Now, you place the ball on any side of this billiard table and decide the slope of the line along which the ball starts at the origin. The trajectory

of the ball seems too complex to you, right? In order to simply this question, we will set restriction that the ball should bounce each side exactly

once and return to its start position at last. Under this restriction, can you find such trajectory that the time of ball running along it is shorter

than any other trajectories which satisfy this restriction?

2 输入输出

输入格式

There are N test cases. The number of test cases N is given in the first line of the input file. For each test case, it contains six

integers (you are ensured that the absolute value of all the integers are less than) which specify the vertex point coordinates of the

acute triangle.

输出格式

You should output the length of the shortest trajectory.The answer should be accurate to three fractional digits exactly one line for each test case.

3 样例

样例输入

2

0 0 2 0 1 2

0 0 2 0 1 3

样例输出

3.200

3.600

4 分析

参考：

http://blog.sina.com.cn/s/blog_493bff030100041r.html

题目要求：

求小球经过两次反射后，回到出发点的路径的最小值。也就是三角形DEF周长的最小值。

题目要求小球和每边碰撞且只碰一次，最后回到出发点

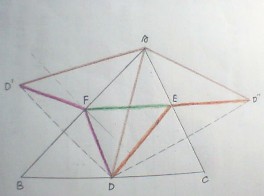
设小球路线在BC,AC,AB上的点为D,E,F

D关于AB,AC的对称点为D',D''

根据对称，我们可以知道

DF = D’F

DE = D”E

AD = AD’= AD”

那么，求⊿DEF的周长可以转化为求折线D’F + FE + ED”的长度

又由于两个等腰三角形⊿ADD’和⊿ADD”,有下面的角度关系：

∠D’AD” = ∠D’AB + ∠BAD + ∠DAC + ∠CAD” = 2∠BAD + 2∠DAC = 2∠A

猜想：如果AD尽可能短，折线变成直线的话，那么所求就是最短的了。（可以想到垂线是最短的）

下面是具体的证明过程：

（1）将D, E两点视为定点，求 DF + EF 的最小值　　见图2

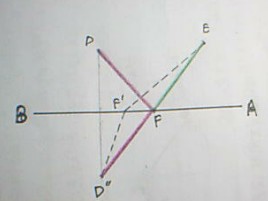
找点D关于边AB的对称点D”,当F为 D”E与AB的交点时,DF + EF的值最小，

有　　∠DFB = ∠D”FB = ∠EFA

同理，将D, F两点视为定点, 有　　∠CED = ∠AEF 将E, F两点视为定点, 有　　∠BDF = ∠CDE

见图3

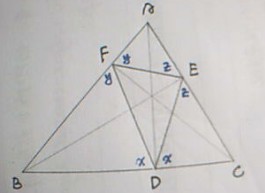
A + y + z = B + y + x = C + x + z = 180°

而　A + B + C = 180°

解得：x = A, y = B, z = C

（2） 设⊿DEF为垂足三角形，那么

因为AD, BE, CF为三高，B, D, E, A四点共圆，则有：∠CED = ∠B （角B+角BAD=90°=角CED+角BED，根据圆周角定理角BED=角BAD）

C, E, F, B四点共圆，则有： ∠AEF = ∠B

故：　∠CED =　∠AEF = ∠B

同理：∠BDF = ∠CDE = ∠A, ∠AFE = ∠BFD = ∠C

见图4　

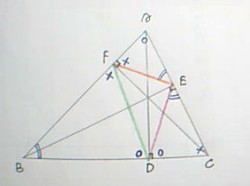
（3） 由(1)和(2)可知，⊿DEF为垂足三角形时，所得周长最短。

计算公式：

见图5

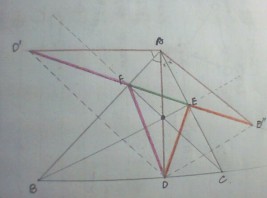
等腰三角形AD’D”中，

D’D”　= 2 * AD * sinA ( 或2 * BE * sinB 或2 * CF * sinC )

AD = b * c * sinA / a //面积公式

故D’D”　= 2 * b * c * (1-cosA * cosA) / a; //cos可以由余弦定理求得

由上即可计算结果。

牛牛们的计算方法：

(1) D’D”= a * cosA + b * cosB + c * cosC ( gg, llyy, index等牛牛)

(2) D’D”= ( (a^2* b^2+b2 * c^2 + c^2 * a^2) – (a^4 + b^4 + c^4)/2.0 )/(abc) ( mathsoft, c0053，jfvp等牛牛)

(3) D’D”= 8 * area * area / ( abc) ( pear 等牛牛)

大家有兴趣可以自己证明一下，好好领会牛牛们的超级思维。收获肯定很大～～～

5 code

#include<iostream>
#include<cmath> //sqrt
using namespace std;

double leng(int a1,int b1,int a2,int b2){
    return sqrt(pow(a1-a2,2)+pow(b1-b2,2)); //pow
}

int main(){
    int a1,b1,a2,b2,a3,b3;
    double a,b,c,cosa,ans;
    int T;
    cin>>T;
    while(T){
        cin>>a1>>b1>>a2>>b2>>a3>>b3;
        a=leng(a1,b1,a2,b2);
        b=leng(a1,b1,a3,b3);
        c=leng(a2,b2,a3,b3);
        cosa=(b*b+c*c-a*a)/(2*b*c);
        ans=2*b*c*(1-cosa*cosa)/a;
        printf("%.3lf\n",ans);

        T--;
    }
return 0;
}