数理统计10（习题篇）：寻找UMVUE

利用L-S定理，充分完备统计量法是寻找UMVUE的最方便方法，不过实际运用时还需要一些小技巧，比如如何写出充分完备统计量、如何找到无偏估计、如何求条件期望，等等。课本上的例题几乎涵盖了所有这些技巧，我们今天以一些课后习题为例，解析这些技巧的实际运用。由于本系列为我独自完成的，缺少审阅，如果有任何错误，欢迎在评论区中指出，谢谢！

Part 1：寻找充分统计量
Part 2：无偏修正
Part 3：待定系数
Part 4：无偏估计的条件期望
附代码

Part 1：寻找充分统计量

不论是使用什么方法，UMVUE首先必须是充分统计量的函数，因此找到充分统计量是必要的，如果是指数族，充分统计量还就是完备统计量。单总体情况下，运用因子分解定理寻找充分统计量已经不陌生，这里给出一个双总体情况下的例子。

第一题（34）：设$X_1,\cdots,X_m\stackrel{\text{i.i.d.}}\sim N(\mu,\sigma^2)$，$Y_1,\cdots,Y_n\stackrel{\text{i.i.d.}}\sim N(\mu,2\sigma^2)$，且两组样本相互独立。试求$\mu,\sigma^2$的充分统计量。

要求充分统计量，其步骤一定是写出概率函数，在这里就是样本联合密度函数。由于两组样本相互独立，即每一个样本之间都是相互独立的，所以联合密度函数就是每一个密度相乘。以下，我们用$\bar X,\bar Y$代表两组样本的样本均值，$S^2_x,S^2_y$代表两组样本的样本方差，另外，离差平方和会是常用于正态分布的量，因此引入它们。

\[Q^2_x=(m-1)S_x^2=\sum_{j=1}^m(X_j-\bar X)^2,\\
Q_y^2=(n-1)S_y^2=\sum_{j=1}^n(Y_j-\bar Y)^2.
\]

现在来写出样本联合密度函数。

\[\begin{aligned}
f(\boldsymbol{x},\boldsymbol{y})&=\left(\frac{1}{\sqrt{2\pi\sigma^2}} \right)^{m}\left(\frac{1}{\sqrt{4\pi\sigma^2}} \right)^n\exp\left\{-\frac{\sum_{j=1}^m(x_j-\mu)^2}{2\sigma^2}-\frac{\sum_{j=1}^n(y_j-\mu)^2}{4\sigma^2} \right\}\\
&=\frac{C}{\sigma^{m+n}}\exp\left\{-\frac{2\sum_{j=1}^mx_j^2+\sum_{j=1}^n y_j^2}{4\sigma^2}+\frac{\mu(2m\bar x+n\bar y)}{2\sigma^2}-\frac{\mu^2(2m+n)}{4\sigma^2} \right\} \\
&=\frac{Ce^{-\frac{\mu^2(2m+n)}{4\sigma^2}}}{\sigma^{m+n}}\exp\left\{ -\frac{1}{4\sigma^2}\left(2\sum_{j=1}^mx_j^2+\sum_{j=1}^ny_j^2 \right)+\frac{\mu}{2\sigma^2}(2m\bar x+n\bar y) \right\}.
\end{aligned}
\]

令

\[\theta_1=-\frac{1}{4\sigma^2},\quad \theta_2=\frac{\mu}{2\sigma^2},
\]

则

\[T_1=2\sum_{j=1}^mX_j^2+\sum_{j=1}^nY_j^2,\quad T_2=2m\bar X+n\bar Y
\]

是$(\theta_1,\theta_2)$的充分完全统计量，接下来对它们做无偏修正得到UMVUE。由于对正态分布$Z\sim N(\mu,\sigma^2)$而言，$\mathbb{E}(Z^2)=\mu^2+\sigma^2$，所以

\[\mathbb{E}(T_1)=2m(\mu^2+\sigma^2)+n(\mu^2+2\sigma^2)=(2m+n)\mu^2+2(m+n)\sigma^2,\\
\mathbb{E}(T_2)=(2m+n)\mu,\\
\mathbb{E}(T_2^2)=4m^2\mathbb{E}(\bar X^2)+n^2\mathbb{E}(\bar Y^2)+4mn\mathbb{E}(\bar X\bar Y)=(2m+n)^2\mu^2+2(2m+n)\sigma^2,\\
\mathbb{E}[T_2^2-(2m+n)T_1]=2(2m+n)(1-m-n)\sigma^2
\]

因此$\mu,\sigma^2$的UMVUE是

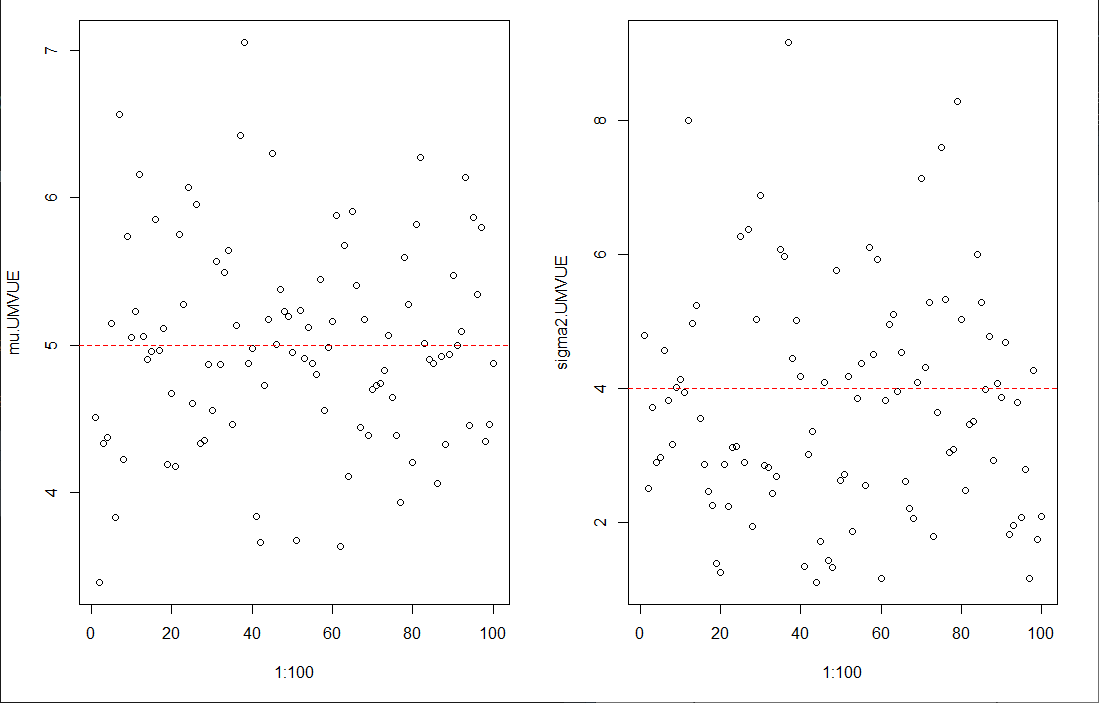
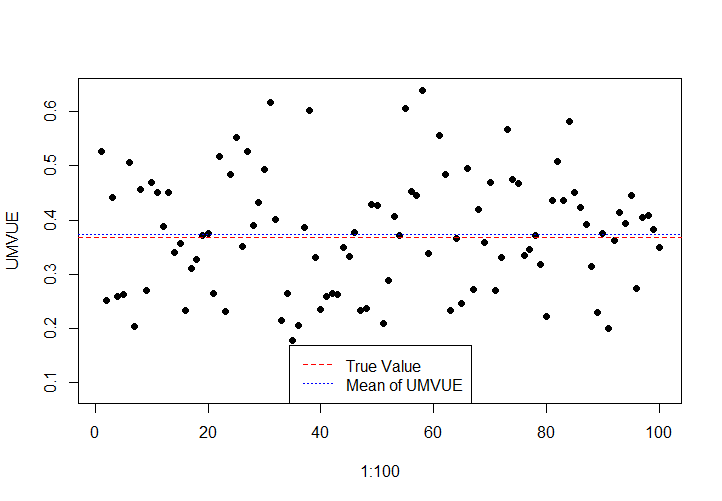
\[\hat\mu=\frac{2m\bar X+n\bar Y}{2m+n},\quad \hat\sigma^2=\frac{T_2^2-(2m+n)T_1}{2(2m+n)(1-m-n)}.
\]

取$\mu=5,\sigma=2$进行模拟。当$m=5,n=6$时，估计量的示意图为：

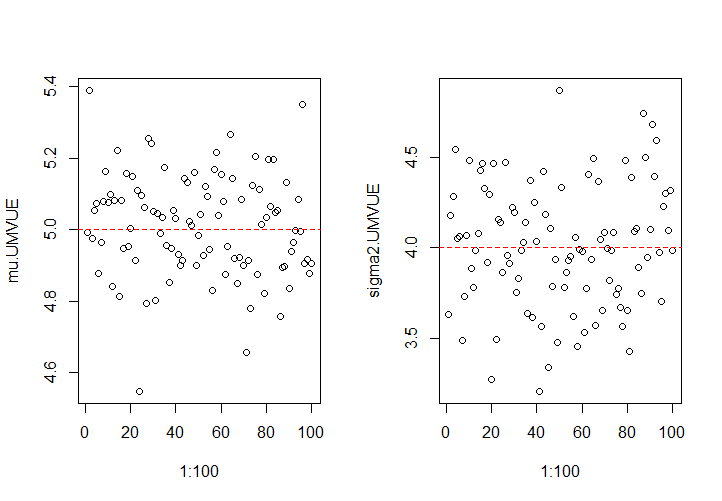
当$m=100,n=200$时，估计量示意图为

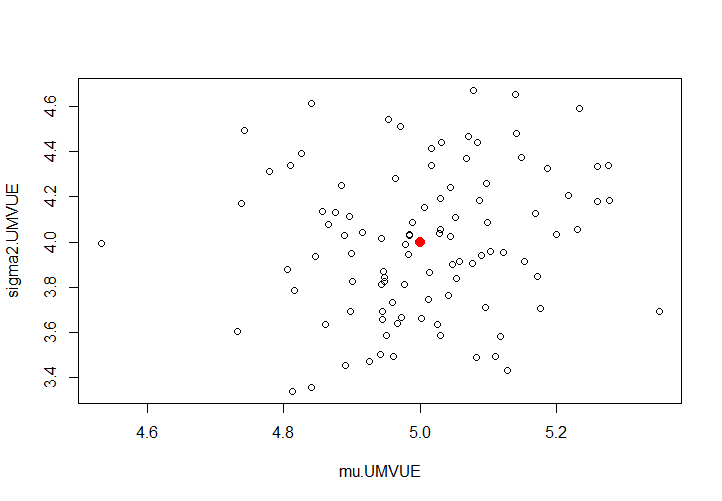
绘制在一张图上：

代码见附录。

Part 2：无偏修正

由于寻找充分完备统计量的过程比较机械，许多时候难点并不在此，而是在于将充分完备统计量进行一定的变换，得到充分完备统计量的无偏函数估计。其关键，就在于将充分完备统计量进行一定的次数变换，达到待估参数所需的次数。

第二题（31） 设$X_1,\cdots,X_n\stackrel{\text{i.i.d.}}\sim N(0,\sigma^2)$，求$\sigma$和$\sigma^4$的UMVUE。

均值已知，容易求得$\sigma^2$的充分完备统计量就是

\[T=\sum_{j=1}^n X_j^2.
\]

关键在于找到合适的$h(\cdot)$，使得$\mathbb{E}(h(T))=\sigma$，或者$\mathbb{E}(h(T))=\sigma^4$。显然，我们会从$\sqrt{T}$和$T^2$上入手，因此，我们需要先给出$T$的密度，才能求其函数的期望。容易发现

\[\frac{T}{\sigma^2}=\sum_{j=1}^n\left(\frac{X_j}{\sigma} \right)^2\sim \chi^2(n)\Rightarrow T\sim \Gamma\left(\frac{n}{2},\frac{1}{2\sigma^2} \right),
\]

所以$T$的密度函数是

\[p(t)=\frac{I_{t>0}}{(2\sigma^2)^{n/2}\Gamma(n/2)}t^{n/2-1}e^{-\frac{t}{2\sigma^2}},
\]

那么$\sqrt{T}$和$T^2$都只作用在$t$的次数上，其期望很容易由$\Gamma$函数的相关性质导出，有

\[\begin{aligned}
\mathbb{E}(\sqrt{T})&=\int_{0}^{\infty}\frac{(\frac{1}{2\sigma^2})^{n/2}}{\Gamma(n/2)}t^{n/2+1/2-1}e^{-\frac{t}{2\sigma^2}}\mathrm{d}t\\
&=\frac{\Gamma(n/2+1/2)}{(\frac{1}{2\sigma^2})^{1/2}\Gamma(n/2)}\int_{0}^\infty\frac{(\frac{1}{2\sigma^2})^{n/2+1/2}}{\Gamma(n/2+1/2)}t^{n/2+1/2-1}e^{-\frac{t}{2\sigma^2}}\mathrm{d}t\\
&=\frac{\Gamma(\frac{n+1}{2})\sigma}{\Gamma(\frac{n}{2})},\\
\mathbb{E}(T^2)&=\int_{0}^{\infty}\frac{(\frac{1}{2\sigma^2})^{n/2}}{\Gamma(n/2)}t^{n/2+2-1}e^{-\frac{t}{2\sigma^2}}\mathrm{d}t\\
&=\frac{\Gamma(n/2+2)}{(\frac{1}{2\sigma^2})^2\Gamma(n/2)}\int_0^{\infty}\frac{(\frac{1}{2\sigma^2})^{n/2+2-1}}{\Gamma(n/2+2)}t^{n/2+2-1}e^{-\frac{t}{2\sigma^2}}\mathrm{d}t\\
&=4\sigma^4\cdot\left(\frac{n}2+1\right)\cdot\frac{n}{2}\\
&=n(n+2)\sigma^4
\end{aligned}
\]

这样就得出了$\sigma$和$\sigma^4$的UMVUE为

\[\hat \sigma=\frac{\Gamma(\frac{n}{2})\sqrt{T}}{\Gamma(\frac{n+1}2)},\\
\widehat{\sigma^4}=\frac{T^2}{n(n+2)}.
\]

第三题（32） 设$X_1,\cdots,X_n\stackrel{\text{i.i.d.}}\sim N(\mu,\sigma^2)$，试求$\mu^2/\sigma^2$的UMVUE。

这里待估参数是两个参数的非线性表达式，这意味着我们要将$\mu$和$\sigma^2$的UMVUE：$\bar X,S^2$进行非线性组合，其关键点就在于正态分布的两个估计量相互独立，因此我们要求的实际上是$\bar X^2,1/S^2$的期望。

由于$\bar X\sim N(\mu,\sigma^2/n)$，所以

\[\mathbb{E}(\bar X^2)=\mu^2+\frac{\sigma^2}{n}.
\]

由于

\[\frac{(n-1)S^2}{\sigma^2}\sim\chi^2(n)\Rightarrow S^2\sim\Gamma\left(\frac{n}{2},\frac{n-1}{2\sigma^2} \right),
\]

所以

\[\begin{aligned}
\mathbb{E}(1/S^2)&=\int_{0}^\infty\frac{(\frac{n-1}{2\sigma^2})^{n/2}}{\Gamma(n/2)}x^{n/2-1-1}e^{-\frac{(n-1)x}{2\sigma^2}}\mathrm{d}x\\
&=\frac{(\frac{n-1}{2\sigma^2})\Gamma(n/2-1)}{\Gamma(n/2)}\int_0^{\infty}\frac{(\frac{n-1}{2\sigma^2})^{n/2-1}}{\Gamma(n/2-1)}x^{n/2-1-1}e^{-\frac{(n-1)x}{2\sigma^2}}\mathrm{d}x\\
&=\frac{n-1}{(n-2)\sigma^2}.
\end{aligned}
\]

由于$\bar X$和$S^2$相互独立，所以

\[\mathbb{E}\left(\frac{\bar X^2}{S^2} \right)=\mathbb{E}(\bar X^2)\mathbb{E}(1/S^2)=\left(\mu^2+\frac{\sigma^2}{n}\right)\frac{n-1}{(n-2)\sigma^2}=\frac{n-1}{n-2}\frac{\mu^2}{\sigma^2}+\frac{n-1}{n(n-2)},
\]

于是

\[\widehat{\frac{\mu^2}{\sigma^2}}=\frac{n-2}{n-1}\left(\frac{\bar X^2}{S^2}-\frac{n-1}{n(n-2)} \right)
\]

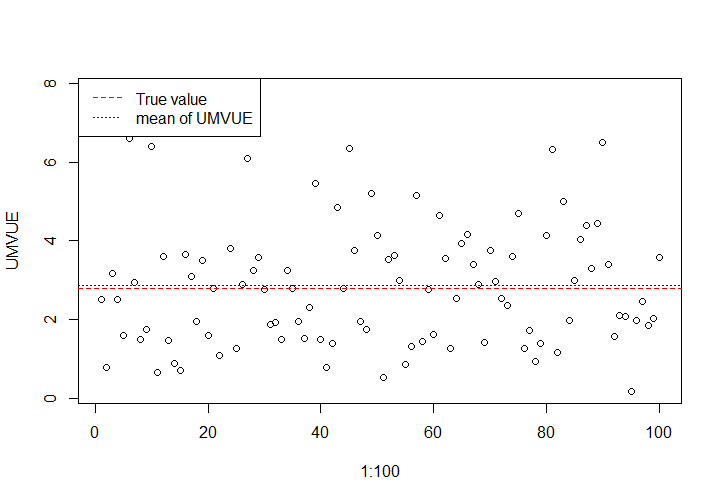
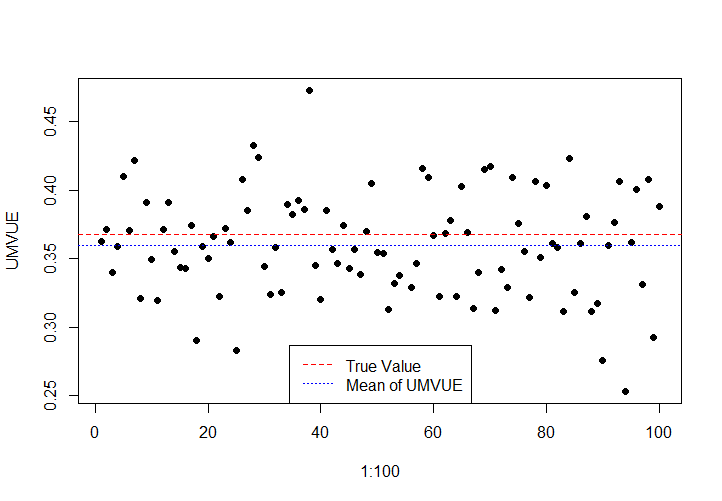
对$\mu=10,\sigma=6$的情况进行模拟，取$n=10$。下图中，红色为真值，蓝色线为100次试验中UMVUE的平均值。

Part 3：待定系数

有时候，无偏估计不是通过简单的升次就能找到的，为了求出符合题意的$h(\cdot)$，可以使用待定系数法。待定系数法假定$h(\cdot)\in\mathcal P(\mathbb{R})$是一个多项式，从而根据次数关系确定$h(\cdot)$的各项系数，即使待估参数不是显然的多项式，也可以通过泰勒展开变成多项式的形式（但一般很少这么做）。

第四题（33） 设$X_1,\cdots,X_n\stackrel{\text{i.i.d.}}\sim B(1,p)$，求$p^s$的UMVUE和$p^s+(1-p)^{n-s}$的UMVUE。

容易验证$p$的UMVUE是$T=\sum_{j=1}^nX_j\sim B(n,p)$，假定$h(T)$是$p^s$的UMVUE，则有

\[\mathbb{E}[h(T)]=\sum_{j=0}^nh(j)C_{n}^j p^j(1-p)^{n-j}=p^s.
\]

左边部分略显繁琐，对其进行整理，得到

\[\sum_{j=0}^nh(j)C_n^j\left(\frac{p}{1-p}\right)^j(1-p)^n=p^s,
\]

所以

\[\sum_{j=0}^nh(j)C_n^j\left(\frac{p}{1-p} \right)^j=\frac{p^s}{(1-p)^n}=\left(\frac{p}{1-p} \right)^s\left(\frac{1}{1-p} \right)^{n-s}.
\]

这里要运用一个二项分布的常用换元：

\[R=\frac{p}{1-p}\Rightarrow p=\frac{R}{R+1},1-p=\frac{1}{R+1}.
\]

将等式两边变成

\[\sum_{j=0}^n h(j)C_n^jR^j=R^s(1+R)^{n-s}=\sum_{k=0}^{n-s}C_{n-s}^kR^{s+k}=\sum_{k=s}^{n}C_{n-s}^{k-s}R^k.
\]

显然$h(j)$不可能含有$R$（因为$R$是未知的），所以

\[h(j)=\left\{\begin{array}l
0,& j=0,1,\cdots,s-1;\\
\frac{C_{n-s}^{j-s}}{C_n^j},& j=s,s+1,\cdots,n.
\end{array}\right.
\]

即

\[\widehat{p^s}=\frac{C_{n-s}^{T-s}}{C_{n}^T},\quad T=s,s+1,\cdots,n
\]

否则$\widehat{p^s}=0$。

对$p^s+(1-p)^s$也是一样的步骤，等式写成

\[\sum_{j=0}^nh(j)C_n^jR^j(1-p)^n=p^s+(1-p)^{n-s},
\]

所以

\[\sum_{j=0}^n h(j)C_n^jR^j=\sum_{k=0}^{n-s}C_{n-s}^k R^{s+k}+\sum_{l=0}^sC_s^l R^l=\sum_{j=0}^{s-1}C_s^jR^j+2R^s+\sum_{j={s+1}}^nC_{n-s}^{j-s}R^{j},
\]

故

\[h(j)=\left\{\begin{array}l
\frac{C_s^j}{C_n^j},&j=0,1,\cdots,s-1;\\
\frac{2}{C_n^j},&j=s;\\
\frac{C_{n-s}^{j-s}}{C_n^j},& j=s+1,\cdots,n.
\end{array}\right.
\]

所以

\[\widehat{p^s+(1-p)^{n-s}}=\left\{\begin{array}l
\dfrac{C_s^T}{C_n^T},&T=0,1,\cdots,s-1;\\
\dfrac{2}{C_n^T},&T=s;\\
\dfrac{C_{n-s}^{T-s}}{C_n^T},& T=s+1,\cdots,n.
\end{array}\right.
\]

Part 4：无偏估计的条件期望

最后这种方法，比起待定系数法更巧一些。对于某些待估参数$g(\theta)$，如果它能用某一事件的概率来表示，就用样本表示出这样的事件$A$，于是$I_A$作为随机变量的期望就是$\mathbb{E}(I_A)=\mathbb{P}(A)=g(\theta)$。在此基础上，如果我们知道某个充分完备统计量$T$，就可以构造$h(T)=\mathbb{E}(I_A|T)$，$h(T)$就是$g(\theta)$的UMVUE。

第五题（36） $X_1,\cdots,X_n$是从指数分布$E(\lambda)$中抽取的简单随机样本，对于给定的$\tau>0$，求$e^{-\lambda \tau}$的UMVUE。

显然$\lambda$的充分完备统计量是$T=\sum_{j=1}^n X_j\sim \Gamma(n,\lambda)$。解题的关键是题目给出的提示：$e^{-\lambda\tau}=\mathbb{P}(X_1>\tau)$，因此构建示性变量$I_{X_1>\tau}$，$e^{-\lambda\tau}$的UMVUE就是$\mathbb{E}[I_{X_1>\tau}|T]$，这里$T-X_1\sim \Gamma(n-1,\lambda)$。

解决这类问题，一般要先写出条件期望并转化为条件概率，然后利用样本的独立性写出等价条件；如果是离散型的，则使用概率函数的求和，如果是连续型的，则使用密度函数的积分。

\[\begin{aligned}
\mathbb{E}[I_{X_1>\tau}|T=t]&=\mathbb{P}(X_1>\tau|T=t)\\
&=\int_{\tau}^{t}\frac{p_{X_1}(x)p_{T-X_1}(t-x)}{p_{T}(t)}\mathrm{d}x \\
&=\int_{\tau}^t\frac{\lambda e^{-\lambda x}\frac{\lambda ^{n-1}}{\Gamma(n-1)}{(t-x)}^{n-2}e^{-\lambda (t-x)}}{\frac{\lambda^n}{\Gamma(n)}t^{n-1}e^{-\lambda t}}\mathrm{d}x\\
&=\frac{1}{t^{n-1}}\int_{0}^{t-\tau}(n-1){x}^{n-2}\mathrm{d}x\\
&=\frac{(t-\tau)^{n-1}}{t^{n-1}}.
\end{aligned}
\]

所以$e^{-\lambda \tau}$的UMVUE是

\[\left(1-\frac{\tau}{T} \right)^{n-1}.
\]

取$\lambda=3,\tau=1/3$进行模拟。以下是$n=10$时的模拟结果：

以下是$n=100$时的模拟结果：

上文中提到的UMVUE寻找方法，都是实践中较为常用的方法，需要掌握。求出UMVUE后，可能还要计算其效率，验证是否有效，这时候只要算出UMVUE的方差与C-R下界进行对比即可。

附代码

第一题：

rm(list=ls())

mu.UMVUE <- c()

sigma2.UMVUE <- c()

mu <- 5

sigma <- 2

m <- 100

n <- 200

for (j in 1:100){

  xlst <- rnorm(m, mu, sigma)

  ylst <- rnorm(n, mu, sigma*sqrt(2))

  T1 <- 2*sum(xlst^2) + sum(ylst^2)

  T2 <- 2*sum(xlst) + sum(ylst)

  mu.UMVUE[j] <- T2 / (2*m+n)

  sigma2.UMVUE[j] <- (T2^2-(2*m+n)*T1) / (2*(2*m+n)*(1-m-n))

}

split.screen(c(1,2))

screen(1)

plot(1:100, mu.UMVUE)

abline(h=c(5), col="red", lty=2)

screen(2)

plot(1:100, sigma2.UMVUE)

abline(h=c(sigma^2), col='red', lty=2)

if (FALSE){

  dev.off()

  plot(mu.UMVUE, sigma2.UMVUE)

  points(5, 4, col="red", cex=2, pch=20)

}

第三题：

rm(list=ls())

n <- 10

UMVUE <- c()

for (j in 1:100){

  xlst <- rnorm(n, 10, 6)

  UMVUE[j] <- (n-2)/(n-1)*(mean(xlst)^2/var(xlst)-(n-1)/(n*(n-2)))

}

plot(1:100, UMVUE)

abline(h=c(100/36), col='red', lty=2)

abline(h=c(mean(UMVUE)), col='blue', lty=3)

legend("topleft", c("True value", "mean of UMVUE"), col=c("red", "blue"), lty=c(2, 3))

第五题：

rm(list=ls())

lambda <- 3

tau <- 1/3

n <- 100

UMVUE <- c()

for (j in 1:100){

  xlst <- rexp(n, lambda)

  UMVUE[j] <- (1-tau/sum(xlst))^(n-1)

}

plot(1:100, UMVUE, pch=16)

abline(h=c(exp(-lambda*tau)), lty=2, col="red")

abline(h=c(mean(UMVUE)), lty=3, col="blue")

legend("bottom", c("True Value", "Mean of UMVUE"), col=c("red", "blue"), lty=c(2,3))