dsu on tree 入门

Dus on tree

树上并查集？。 啊这，并不是的啦，他利用了树上启发式合并的思想。

他主要解决不带修改且主要询问子树信息的树上问题。

先来看到例题，CF600E 。

这不就是树上莫队的经典题吗？。 会莫队的大佬一眼就秒了。

不会的蒟蒻我只能打打暴力，骗骗分。

首先，我们暴力其实很好打，就是对每个点都统计一下他子树的答案，时间复杂度为 O(\(n^2\)).

这显然，我们是不能接受的，我们需要优化。

Dus on tree 利用轻重链剖分的思想，把他的复杂度优化为 O(\(n log n\)) 的。

我们递归处理子树的时候，重复计算了很多种状态，我们就要考虑剪枝，减去重复的状态。

实际上，我们最后处理的子树肯定是不需要删除他的贡献的，在计算他的父亲 \(x\) 的答案的时候，直接利用他的信息，

就可以直接推出他父亲的答案。

我们就要确定一种顺序，使我们遍历子树节点的数目尽可能少。

我们选的最后遍历的要为他的重儿子（重儿子子树中的节点是最多的）

就这样 Dus on tree 的算法流程就是:

• 递归处理每个轻儿子，同时消除轻儿子的影响。

• 递归重儿子，不消除重儿子的影响。

• 统计轻儿子对答案的贡献。

• 将轻儿子和重儿子的信息合并，得出这个节点的答案。

• 消除轻儿子对答案的影响

大致的代码张这样:

void dfs(int x,int fa,int opt)
{
    for(int i = head[x]; i; i = e[i].net)
    {
        int to = e[i].to;
        if(to == fa || to == son[x]) continue;
        dfs(to,1);//递归轻儿子
    }
    if(son[x]) dfs(son[x],0);//帝国重儿子
    add(x);//统计轻儿子对答案的贡献
    ans[x] = now_ans;//合并轻儿子和重儿子得出这个点的答案
    if(opt == 1) delet(x);//如果他是轻儿子，消除他的影响
}

图例长这样

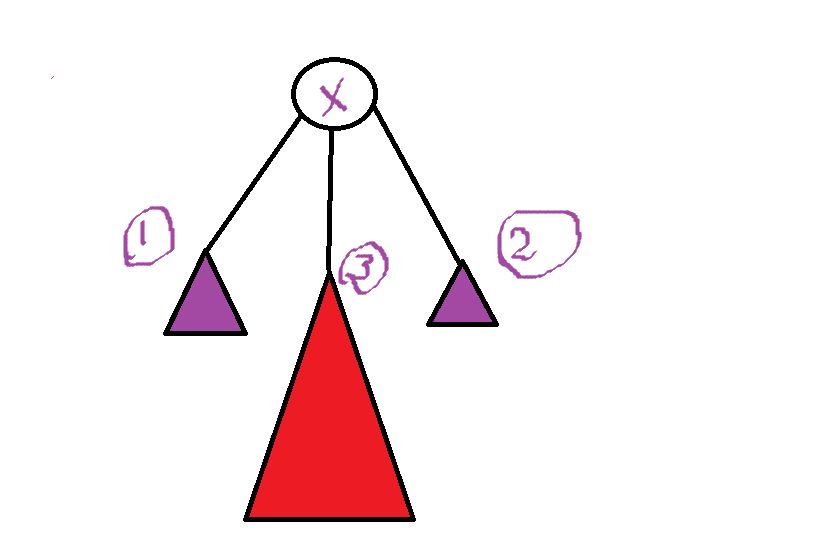
紫色的是他的轻儿子，红色的是他的重儿子，序号是他的遍历顺序。

这不是和普通的爆搜没什么区别吗？为什么复杂度不是O（\(n^2\)）

下面，我们简单证明一下他的复杂度，不愿意看的可以直接跳过。

性质：一个节点到根的路径上轻边个数不会超过 logn 条

证明：设根到该节点有 \(x\) 的轻边，该节点的大小为 \(y\)，根据轻重边的定义，轻边所连向的点的大小不会成为该节点

总大小的一般。这样每经过一条轻边，\(y\) 的上限就会 /2,所以 \(x\) < \(log n\)

然而这条性质并不能解决问题,我们考虑一个点会被访问多少次

一个点被访问到，只有两种情况

1、在暴力统计轻边的时候访问到。根据前面的性质，该次数 < \(log n\)

2、通过重边 在遍历的时候被访问到,显然只有一次

如果统计一个点的贡献的复杂度为O(1)的话，该算法的复杂度为O(\(nlog n\))

我们上面的例题就可以直接套板子了。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long
const int N = 1e5+10;
int n,m,tot,u,v,max_c,now_ans,heavy_son;
int siz[N],fa[N],son[N],head[N],cnt[N],c[N],ans[N];
struct node
{
    int to,net;
}e[N<<1];
void add_(int x,int y)
{
    e[++tot].to = y;
    e[tot].net = head[x];
    head[x] = tot;
}
inline int read()
{
    int s = 0,w = 1; char ch = getchar();
    while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
    while(ch >= '0' && ch <= '9'){s =s * 10+ch - '0'; ch = getchar();}
    return s * w;
}
void get_tree(int x)
{
    siz[x] = 1;
    for(int i = head[x]; i; i = e[i].net)
    {
        int to = e[i].to;
        if(to == fa[x]) continue;
        fa[to] = x;
        get_tree(to);
        siz[x] += siz[to];
        if(siz[son[x]] < siz[to]) son[x] = to;
    }
}
void add(int x,int val)
{
    cnt[c[x]] += val;
//    printf("----------->\n");
//    cout<<max_c<<" "<<now_ans<<endl;
    if(cnt[c[x]] > max_c)//max_c 记录当前出现次数最多的颜色的出现次数
    {
        max_c = cnt[c[x]];
        now_ans = c[x];
    }
    else if(cnt[c[x]] == max_c)//相等的话，记录一下编号和
    {
    	now_ans += c[x];
    }
    for(int i = head[x]; i; i = e[i].net)
    {
        int to = e[i].to;
        if(to == fa[x] || to == heavy_son) continue;
        add(to,val);
    }
}
void dfs(int x,int type)
{
    for(int i = head[x]; i; i = e[i].net)
    {
        int to = e[i].to;
        if(to == fa[x] || to == son[x]) continue;
        dfs(to,1);
    }
    if(son[x])
    {
    	dfs(son[x],0);
    	heavy_son = son[x];
    }
    add(x,1);
    ans[x] = now_ans;
    heavy_son = 0;
    if(type == 1)
    {
    	add(x,-1);
    	max_c = now_ans = 0;
    }
}
signed main()
{
    n = read();
    for(int i = 1; i <= n; i++) c[i] = read();
    for(int i = 1; i <= n-1; i++)
    {
        u = read(); v = read();
        add_(u,v); add_(v,u);
    }
    get_tree(1); dfs(1,0);
    for(int i = 1; i <= n; i++) printf("%lld ",ans[i]);
    return 0;
}

一个需要注意的点是 不能记录出现次数最多的颜色编号，而应该记录这个颜色出现的次数。（我在这里卡了好几回）

因为你这样会重复计算，第二组样例就是一组 很好的 Hack 数据。