Simulink仿真入门到精通（十五） Simulink在流程工业中的仿真应用

15.1 工业乙醇生产与计算机仿真

乙醇作为可再生清洁能源不仅可以代替四乙基铅作为汽油的防爆剂，还可以制造汽油醇。这一巨大的潜在需求促使人们去寻找提高乙醇工业生产率的途径，使人们着手于发酵工程的研究。微生物学、发酵研究的发展，使微生物反应过程的种类和规模不断扩大，其应用也深入到多个工业领域，然而由于反应涉及活细胞的参与，菌体生长及产物生成等机理复杂多变，目前尚难为人们所了解和把握，更难以进行统一的描述。人们一般通过实验的方法寻找微生物的生长规律，通过数值分析和拟合了解发酵过程的规律。这样的做法周期性长，需要消耗的资源多，且无法在短时间内对工业流程中出现的问题提出及时的应对方案。

计算机仿真技术作为分析和研究系统运行行为、揭示系统动态过程和运动规律的一种重要手段和方法，随着系统科学研究的深入，以及控制理论、计算技术、计算机科学与技术的发展而形成一门新兴的学科。近年来，随着信息处理技术的突飞猛进，仿真技术得到迅速发展。“仿真是一种基于模型的活动”，设计多学科、多领域的知识和经验。成功进行仿真研究的关键是有机、协调地组织实施仿真全生命周期的各类活动。这里的“各类活动”，就是指“系统建模”、“仿真建模”、“仿真实验”，联系这些活动的要素是“系统”、“模型”、“计算机”。其中，系统是研究的对象，模型是系统的抽象，仿真是为了通过对模型的实验达到跟真实系统对比并接近于研究其特性的目的。

15.2 工业乙醇发酵流程

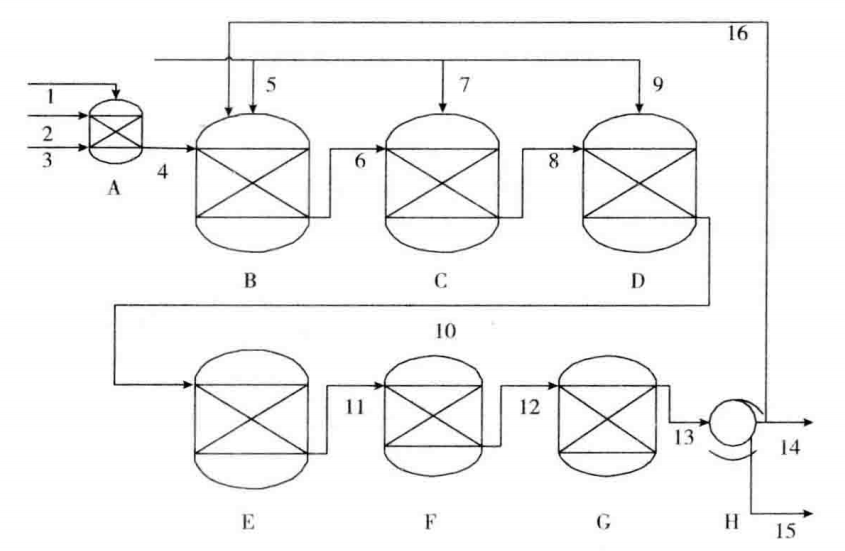
A：预发酵罐

B~G：6个发酵罐

H：离心分离机

1、5、7、9：干法糖液

2：营养液

3：酵母

15：产品，含11%~12%的乙醇

14：废酵母，其中一部分循环回去

发酵温度31~33℃。

15.3 乙醇发酵动力学方程

1. 葡萄糖液在酵母作用下分解产生乙醇；
2. 酵母细胞本身吸收葡萄糖液来促进自身生长。

\[\begin{array}{l}
\frac{{{\rm{d}}x}}{{{\rm{d}}t}} = \mu x\\
\frac{{{\rm{d}}p}}{{{\rm{d}}t}} = \upsilon x\\
\frac{{{\rm{d}}s}}{{{\rm{d}}t}} = - (\alpha + \beta )x
\end{array}\]

1. 对每个发酵罐，发酵液流入量=流出量；
2. 对每种物质而言，其质量变化=流入/流出质量变化+反应生成/消耗质量变化。

\[\begin{array}{l}
{F_{in}} = {F_{out}}\\
\frac{{{\rm{d}}x}}{{{\rm{d}}t}} = \mu x + D({x_0} - x)\\
\frac{{{\rm{d}}p}}{{{\rm{d}}t}} = \upsilon x + D({p_0} - p)\\
\frac{{{\rm{d}}s}}{{{\rm{d}}t}} = - (\frac{\mu }{{{Y_{x/s}}}} + \frac{\upsilon }{{{Y_{p/s}}}})x + D({p_0} - p)
\end{array}\]

因为实际生产过程中基质浓度较高，需要考虑底物和产物对细胞生长的抑制作用。

\[\begin{array}{l}
\mu = {\mu _{\max }}\frac{S}{{{K_s} + S + {s^2}/{K_{sl}}}} \cdot \frac{{{K_p}}}{{{K_p} + p + {p^2}/{K_{pl}}}}\\
\upsilon = {\upsilon _{\max }}\frac{S}{{{K_{sp}} + S + {s^2}/{K_{spl}}}} \cdot \frac{{{K_{pp}}}}{{{K_{pp}} + p + {p^2}/{K_{ppl}}}}
\end{array}\]

发酵过程模型流程图：

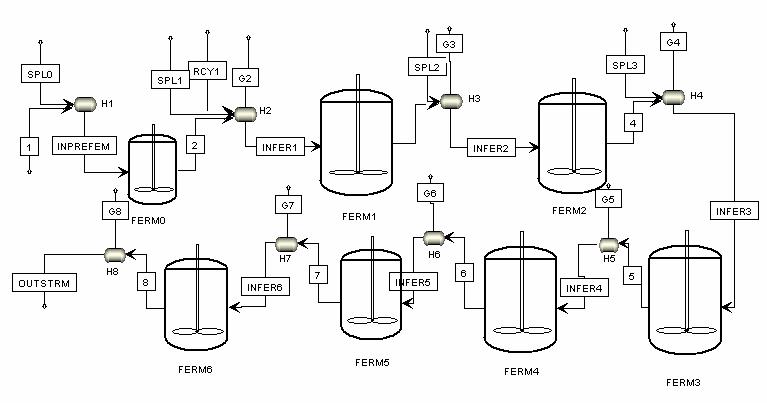
15.4 MATLAB求解

• [T,Y]=solver(odefun,tspan,y0,options,p1,p2,...)

参考：https://ww2.mathworks.cn/help/matlab/ref/ode45.html

solver为命令ode45、ode23、ode113、ode15s、ode23s、ode23t、ode23tb之一，odefun为显式常微分方程dy/dt=f(t,y)或包含混合矩阵的方程M(t,y)×dy/dt=f(t,y)。命令ode23只能求解常数混合矩阵的问题；命令ode23t与ode15s可以求解奇异矩阵的问题。tspan为积分区间的向量，tspan=[t0,tf]。要获得问题在指定时间点t0、t1、t2、...上的解，可以令tspan=[t0,t1,t2,...,tf]，但必须是单调的。y0为包含初值条件的向量，options为用命令odeset设置的可选积分参数。p1、p2、...为传递给函数odefun的可选参数。

function f=func(t,n,V)          %发酵罐的动力学函数,输入参数为时间,输入矩阵,体积
global x0 p0 s0 Yxs Yps umax vmax Ks Kps Kp Kpp Ksi Kpsi Kpi Kppi T F Vy
f=zeros(3,1);                             %按照三行扩展列来保存每一步的三种物料的浓度
u=umax*n(3)/(Ks+n(3)+n(3)^2/Ksi)*Kp/(Kp+n(2)+n(2)^2/Kpi);
v=vmax*n(3)/(Kps+n(3)+n(3)^2/Kpsi)*Kpp/(Kpp+n(2)+n(2)^2/Kppi);
D=Vy/V;
f(1)=u*n(1)+D*(x0-n(1));                %Dx         n(1)-x,n(2)-p,n(3)-s
f(2)=v*n(1)+D*(p0-n(2));                %Dp
f(3)=-(u/Yxs+v/Yps)*n(1)+D*(s0-n(3));        %Ds

也可以用龙格-库塔法求解，四阶示例如下。

function [x,y]=runge_kutta1(ufunc,y0,h,a,b,Vg)    %参数表顺序依次是微分方程组的函数名称，初始值向量，步长，时间起点，时间终点,发酵罐体积
n=floor((b-a)/h);                                    %求步数
x(1)=a;                                       %时间起点
y(:,1)=y0;                                    %赋初值，可以是向量，但是要注意维数
for ii=1:n
   x(ii+1)=x(ii)+h;
   k1=ufunc(x(ii),y(:,ii),Vg);
   k2=ufunc(x(ii)+h/2,y(:,ii)+h*k1/2,Vg);
   k3=ufunc(x(ii)+h/2,y(:,ii)+h*k2/2,Vg);
   k4=ufunc(x(ii)+h,y(:,ii)+h*k3,Vg);
   y(:,ii+1)=y(:,ii)+h*(k1+2*k2+2*k3+k4)/6;       %按照龙格库塔方法进行数值求解
end

>> [x,y]=runge_kutta1(@func,[10;0;200],0.1,0,15,500);
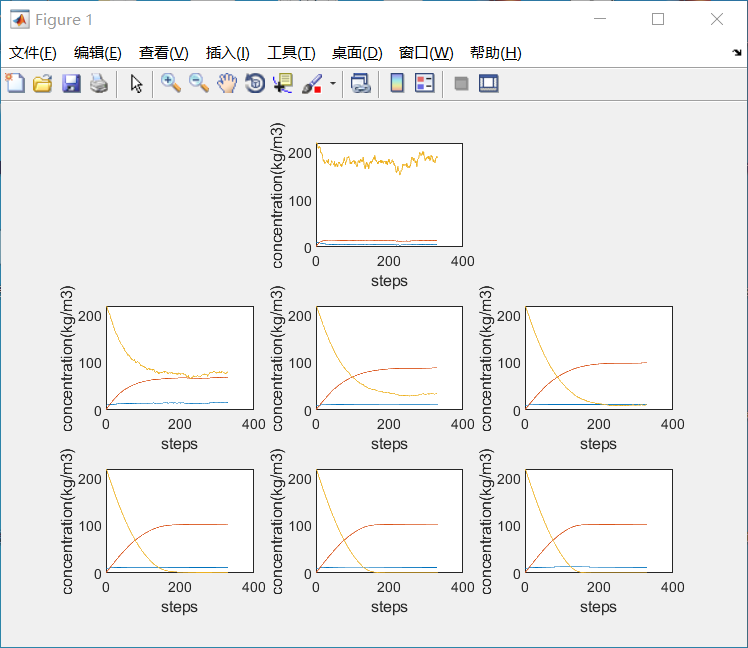
>> plot(x,y);
>> legend({'酵母菌体','乙醇','葡萄糖液'});

15.5 Simulink求解

Simulink常用的微分方程解法：

1. 根据方程搭建模型，较为复杂，通用；
2. 用S函数，需要求解状态方程；
3. 用传输函数，对时域方程进行拉普拉斯变换；
4. 向量法，用Fcn模块表示一个微分方程中的一位输入，三个Fcn模块并联。

15.6 连续流程仿真

15.7 GUIDE设计

15.7.1 GUIDE介绍

在命令窗口输入guide。

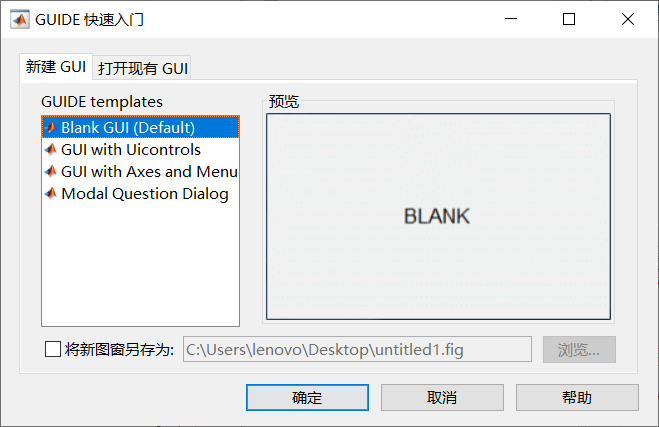
例：设计按钮控制图片显示的界面。

拖出axes、pushbutton控件，右击pushbutton，选择View Callbacks→Callback。

% --- Executes on button press in pushbutton1.
function pushbutton1_Callback(hObject, eventdata, handles)
% hObject    handle to pushbutton1 (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
axes(handles.axes1);
imshow('flower.jpg');

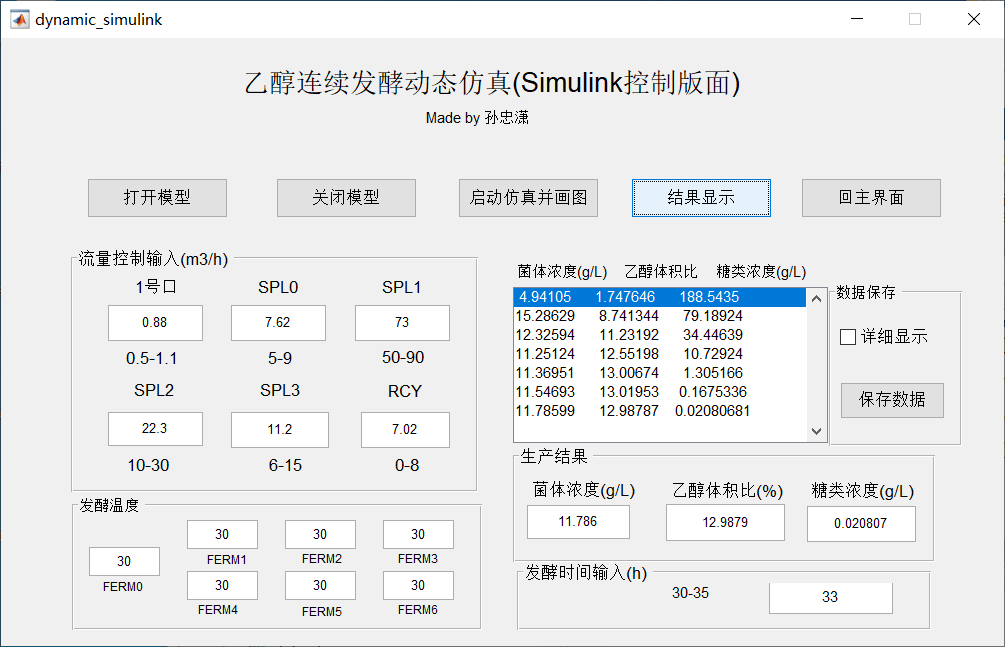
15.7.2 乙醇仿真界面