《Three.js 入门指南》2- 照相机

2.1 什么是照相机

我们使用Three.js创建的场景是三维的，而通常情况下显示屏是二维的，那么三维的场景如何显示到二维的显示屏上呢？照相机就是这样一个抽象，它定义了三维空间到二维屏幕的投影方式，用“照相机”这样一个类比，可以使我们直观地理解这一投影方式。

而针对投影方式的不同，照相机又分为正交投影照相机与透视投影照相机。我们需要为自己的程序选择合适的照相机。

简单的来说，就是在2维的屏幕上，实现3维的画面效果。

2.2正交投影 vs 透视投影

什么是正交投影和透视投影？

如图（a），透视投影更贴近我们实际生活中，人眼视觉感受，更加合理，真实。其特点是“近大远小”

如图（b），正交投影，即我们数学概念上的立体图形，我们不考虑显示生活中，该物体给我们人眼的实际视觉感受，仅客观的展现其形状特性。其特点是“在三维空间内平行的线，投影到二维空间中也一定是平行的”。

同一个立体物体，通过透视投影和正交投影，给我们的实际视觉感受并不相同。

怎么判断我需要正交投影还是透视投影？

一般说来，对于制图、建模软件通常使用正交投影，这样不会因为投影而改变物体比例；而对于其他大多数应用，通常使用透视投影，因为这更接近人眼的观察效果。

2.3正交投影相机和透视投影相机的参数说明

正交投影相机

参数介绍

正交投影照相机（Orthographic Camera）设置起来较为直观，它的构造函数是：

THREE.OrthographicCamera(left, right, top, bottom, near, far)

这六个参数分别代表正交投影照相机拍摄到的空间的六个面的位置，这六个面围成一个长方体，我们称其为视景体（Frustum）。只有在视景体内部（下图中的灰色部分）的物体才可能显示在屏幕上，而视景体外的物体会在显示之前被裁减掉。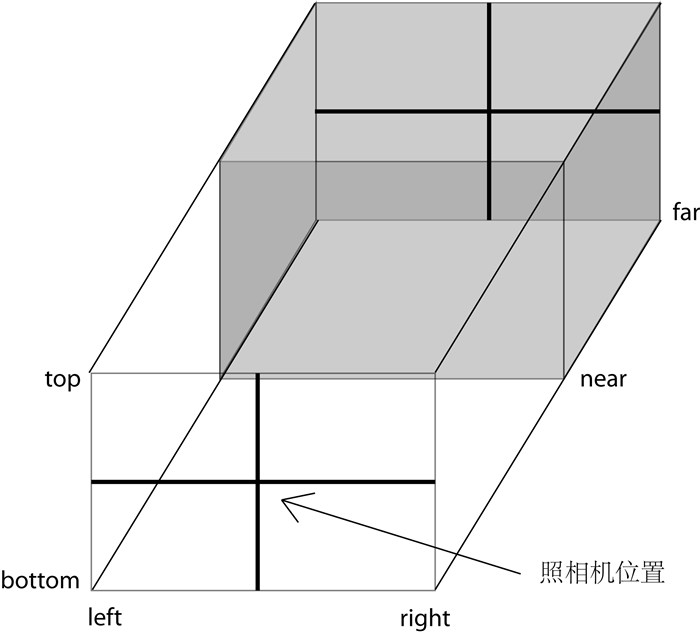

为了保持照相机的横竖比例，需要保证(right - left)与(top - bottom)的比例与Canvas宽度与高度的比例一致。

near与far都是指到照相机位置在深度平面的位置，而照相机不应该拍摄到其后方的物体，因此这两个值应该均为正值。为了保证场景中的物体不会因为太近或太远而被照相机忽略，一般near的值设置得较小，far的值设置得较大，具体值视场景中物体的位置等决定。

透视投影相机

参数介绍

透视投影照相机（Perspective Camera）的构造函数是：

THREE.PerspectiveCamera(fov, aspect, near, far)

让我们通过一张透视照相机投影的图来了解这些参数。

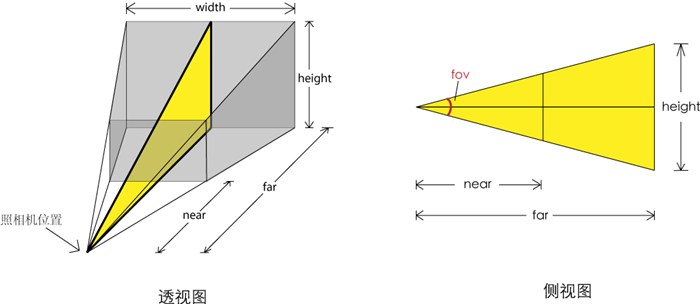
透视图中，灰色的部分是视景体，是可能被渲染的物体所在的区域。fov是视景体竖直方向上的张角（是角度制而非弧度制），如侧视图所示。

aspect等于width / height，是照相机水平方向和竖直方向长度的比值，通常设为Canvas的横纵比例。

near和far分别是照相机到视景体最近、最远的距离，均为正值，且far应大于near。

特别需要注意的一点：

在修改视角的时候，我们一般需要修改这两个参数：

一个是相机的位置：camera.position.set(4, 3, 5);

另一个是相机的镜头瞄准点：camera.lookAt(new THREE.Vector3(0, 0, 0))

而需要注意的地方就是，不论设置了什么，这些设置都应该放在渲染之前，也就是说，renderer.render(scene, camera);该代码需要放在最后，修改视角（别的也是一样）才能够生效。