BinaryTree(二叉树)

　　我认为二叉树的递归实现体现了递归思想的一些重要性质，如果对递归的理解不够的话，想利用递归来实现是很费劲的(实际上我现在都还有些懵...)，虽然会用，但一些地方不能弄清楚原因。

　　经过几天的学习，看了许多前辈们的代码，综合后总算实现了一个二叉查找树，对创建和插入等基本操作上是弄明白并实现了，就是删除还有些细节不是很明白，因此，留着慢慢理解。

　　Head File：

#ifndef _TREE_H_

#define _TREE_H_

#define bool int

#define true 1

#define false 0

typedef int ElemType;

typedef struct Tree

{

    ElemType DATA;            //节点数据

    struct Tree * left;        //右孩子

    struct Tree * right;    //左孩子

    struct Tree * parent;    //双亲

}BiTree, Node;

/* 定义全局函数 */

/* Initialize Binary Tree */

BiTree * InitBiTree(void);            

/* 返回当前二叉树的度 */

int GetDegree(BiTree * T);

/* 返回当前二叉树的深度 */

int GetDepth(BiTree * T);

/* DLR */

void PreorderTraversal(BiTree * T);

/* LDR */

void InorderTraverse(BiTree * T);

/* LRD */

void PostorderTraverse(BiTree * T);

/* 插入节点到二叉树 */

Node * InsertBiTree(BiTree * T, ElemType X);

/* 删除节点 */

Node * DeleteNode(BiTree * T, ElemType X);

/* 清空树 */

void DeleteAll(BiTree * T);

/* 节点之间的关系 */

void FamilyBiTree(BiTree * T, ElemType y);

#endif

　　Operation Function:

#include <stdio.h>

#include <stdlib.h>

#include "tree.h"

/* 定义局部函数 */

/* 查找数据节点 */

static Node * Find_(BiTree * T, ElemType X);

/* 查找最小节点 */

static Node * FindMin(BiTree * T);

/* 申请新节点 */

static Node * Malloc_New_Node(BiTree * T, ElemType X);

/* 找到新节点要插入的位置 */

static Node * Insert_Node_Pos(BiTree * T, Node * Pos);

/* 找到比删除的节点数据大的最小节点 */

static Node * BiTree_(Node * p);

/* 删除节点后对节点的处理 */

static Node * Delete_Node_Pos(BiTree * T, Node * Pos);

/* Operation function */

BiTree * InitBiTree(void)

{

    BiTree * T;

    T = NULL;

    return T;

}

int GetDegree(BiTree * T)

{

    if(T == NULL)

        return 0;

    return GetDegree(T -> left) + GetDegree(T -> right) + 1;

}

int GetDepth(BiTree * T)                //返回当前二叉树的深度

{

    int depthLeft, depthRight;

    if(T == NULL)

        return 0;

    depthLeft = GetDepth(T -> left);

    depthRight = GetDepth(T -> right);

    return (depthLeft > depthRight ? (depthLeft + 1) : (depthRight + 1));

}

void PreorderTraversal(BiTree * T)        //前序遍历

{

    if(T != NULL)

    {

        printf("%d ", T -> DATA);

        PreorderTraversal(T -> left);

        PreorderTraversal(T -> right);

    }

}

void InorderTraverse(BiTree * T)        //中序遍历

{

    if(T != NULL)

    {

        InorderTraverse(T -> left);

        printf("%d ", T -> DATA);

        InorderTraverse(T -> right);

    }

}

void PostorderTraverse(BiTree * T)        //后序遍历

{

    if(T != NULL)

    {

        PostorderTraverse(T -> left);

        PostorderTraverse(T -> right);

        printf("%d ", T -> DATA);

    }

}

Node * InsertBiTree(BiTree * T, ElemType X)

{

    Node * inNodePos;

    if((inNodePos = Malloc_New_Node(T, X)) == NULL)

        return T;

    return Insert_Node_Pos(T, inNodePos);

}

static Node * Malloc_New_Node(BiTree * T, ElemType X)

{

     Node * p;

     if((p = malloc(sizeof(Node))) == NULL)

     {

        fprintf(stderr, "Malloc() error!\n");

        return NULL;

     }

     p -> DATA = X;

     p -> parent = p -> left = p -> right = NULL;

     return p;

}

static Node * Insert_Node_Pos(BiTree * T, Node * Pos)

{

    Node * p, * q;

    p = NULL;

    q = T;

    while(q != NULL)

    {

        p = q;

        if(Pos -> DATA < q -> DATA)

            q = q -> left;

        else if(Pos -> DATA > q -> DATA)

            q = q -> right;

        else        // 相同

            break;

    }

    Pos -> parent = p;

    if(p == NULL)

        T = Pos;

    else if(Pos -> DATA < p -> DATA)

        p -> left = Pos;

    else if(Pos -> DATA > p -> DATA)

        p -> right = Pos;

    return T;

}

static Node * Find_(BiTree * T, ElemType X)

{

    if(T == NULL)

    {

        fprintf(stderr, "Nothing!\n");

        return NULL;

    }

    else if(X < T -> DATA)

        return Find_(T -> left, X);

    else if(X > T -> DATA)

        return Find_(T -> right, X);

    else

        return T;

}

static Node * FindMin(BiTree * T)

{

    if(T == NULL)

        return NULL;

    else if(T -> left == NULL)

        return T;

    else

        return FindMin(T -> left);

}

Node * DeleteNode(BiTree * T, ElemType X)

{

    Node * temp;

    if((temp = Find_(T, X)) != NULL)

        T = Delete_Node_Pos(T, temp);

    return T;

}

static Node * BiTree_(Node * p)

{

    Node * q;

    if(p -> right != NULL)

        return FindMin(p -> right);

    q = p -> parent;

    while(q != NULL && p == q -> right)

    {

        p = q;

        q = q -> parent;

    }

    return q;

}

static Node * Delete_Node_Pos(BiTree * T, Node * Pos)

{

    Node * p = NULL, * q = NULL;

    if(!(Pos -> left || Pos -> right))

        q = Pos;

    else

        q = BiTree_(Pos);

    if(q -> left != NULL)

        p = q -> left;

    else

        p = q -> right;

    if(p != NULL)

        p -> parent = q -> parent;

    if(q -> parent == NULL)

        T = p;

    else if(q == q -> parent -> left)

        q -> parent -> left = p;

    else

        q -> parent -> right = p;

    if(q != Pos)

        Pos -> DATA = q -> DATA;

    if(q != NULL)

        free(q);

    return T;

}

void DeleteAll(BiTree * T)

{

    if(T != NULL)

    {

        DeleteAll(T -> left);

        DeleteAll(T -> right);

        free(T);

    }

}

/*

 * 强迫症晚期...

 *

 * 如果char类型的数据的话就不会出现输出问题

 *

 * 但这个程序用了int,但是也没想到树中间节点的情况还挺麻烦

 *

 * 为了不看到程序因为节点没有数据的原因被强制终止

 *

 * 于是硬是浪费了一大把时间做这个if...else的判断

 *

 * 写完之后...(扶额...)

 */

void FamilyBiTree(BiTree * T, ElemType y)            // 家谱 共三种情况: 根、树枝、叶子

{

    if(Find_(T, y) -> parent == NULL)        // 根节点的4种情况

    {

        if(Find_(T, y) -> left == NULL    && Find_(T, y) -> right == NULL)//case 1: 无孩子

            printf("\n%d 是根, 没有双亲 无左孩子 无右孩子\n", Find_(T, y) -> DATA);

        else if(Find_(T, y) -> left == NULL)        //case 2: 无左孩子

            printf("\n%d 是根, 没有双亲 无左孩子 右孩子为:%d\n", Find_(T, y) -> DATA, Find_(T, y) -> right -> DATA);

        else if(Find_(T, y) -> right == NULL)        //case 3: 无右孩子

            printf("\n%d 是根, 没有双亲 左孩子为:%d 无右孩子\n", Find_(T, y) -> DATA, Find_(T, y) -> left -> DATA);

        else        // case 4: 两个孩子

            printf("\n%d 是根, 没有双亲 左孩子为:%d 右孩子为:%d\n", Find_(T, y) -> DATA, Find_(T, y) -> left -> DATA, Find_(T, y) -> right -> DATA);

    }

    else if((Find_(T, y) -> left == NULL && Find_(T, y) -> right == NULL) && Find_(T, y) -> parent != NULL)    //叶节点的4种情况

    {

        if(Find_(T, y) -> parent -> left == NULL)    //case 1: 无左兄弟

            printf("\n%d 是叶节点无左孩子、右孩子, 双亲为:%d 无左兄弟 右兄弟为自己本身: %d\n", Find_(T, y) -> DATA, Find_(T, y) -> parent -> DATA, Find_(T, y) -> parent -> right -> DATA);

        else if(Find_(T, y) -> parent -> right == NULL)    //case 2: 无右兄弟

            printf("\n%d 是叶节点无左孩子、右孩子, 双亲为:%d 左兄弟为自己本身:%d 无右兄弟\n", Find_(T, y) -> DATA, Find_(T, y) -> parent -> DATA, Find_(T, y) -> parent -> left -> DATA);

        else if(Find_(T, y) -> parent -> left == NULL && Find_(T, y) -> parent -> right == NULL)    //case 3: 没有兄弟

            printf("\n%d 是最深叶节点无左孩子、右孩子, 双亲为:%d 无左兄弟 无右兄弟\n", Find_(T, y) -> DATA, Find_(T, y) -> parent -> DATA);

        else            // case 4: 有两个兄弟

            printf("\n%d 是叶节点无左孩子、右孩子, 双亲为:%d 左兄弟%s:%d 右兄弟%s:%d\n", Find_(T, y) -> DATA, Find_(T, y) -> parent -> DATA, (y == Find_(T, y) -> parent -> left -> DATA ? "为自己本身" : " "), Find_(T, y) -> parent -> left -> DATA, (y == Find_(T, y) -> parent -> right -> DATA ? "为自己本身" : " "), Find_(T, y) -> parent -> right -> DATA);

    }

    else if((Find_(T, y) -> left == NULL || Find_(T, y) -> right == NULL) && (Find_(T, y) -> parent -> left != NULL && Find_(T, y) -> parent -> right != NULL)) // 缺少一个孩子的中间节点

    {

        if(Find_(T, y) -> left == NULL)

            printf("\n%d 的双亲为:%d 无左孩子 右孩子为:%d 左兄弟%s:%d 右兄弟%s:%d\n", Find_(T, y) -> DATA, Find_(T, y) -> parent -> DATA, Find_(T, y) -> right -> DATA, (y == Find_(T, y) -> parent -> left -> DATA ? "为自己本身" : " "), Find_(T, y) -> parent -> left -> DATA, (y == Find_(T, y) -> parent -> right -> DATA ? "为自己本身" : " "), Find_(T, y) -> parent -> right -> DATA);

        else

            printf("\n%d 的双亲为:%d 左孩子为:%d 无右孩子 左兄弟%s:%d 右兄弟%s:%d\n", Find_(T, y) -> DATA, Find_(T, y) -> parent -> DATA, Find_(T, y) -> left -> DATA, (y == Find_(T, y) -> parent -> left -> DATA ? "为自己本身" : " "), Find_(T, y) -> parent -> left -> DATA, (y == Find_(T, y) -> parent -> right -> DATA ? "为自己本身" : " "), Find_(T, y) -> parent -> right -> DATA);

    }

    else if((Find_(T, y) -> left != NULL && Find_(T, y) -> right != NULL) && Find_(T, y) -> parent -> left == NULL)        // 只缺少一个左兄弟的中间节点

        printf("\n%d 的双亲为:%d 左孩子为:%d 右孩子为:%d 无左兄弟 右兄弟为自己本身:%d\n", Find_(T, y) -> DATA, Find_(T, y) -> parent -> DATA, Find_(T, y) -> left -> DATA, Find_(T, y) -> right -> DATA, Find_(T, y) -> parent -> right -> DATA);

    else if((Find_(T, y) -> left != NULL && Find_(T, y) -> right != NULL) && Find_(T, y) -> parent -> right == NULL)    // 只缺少一个右兄弟的中间节点

        printf("\n%d 的双亲为:%d 左孩子为:%d 右孩子为:%d 左兄弟为自己本身:%d 无右兄弟\n", Find_(T, y) -> DATA, Find_(T, y) -> parent -> DATA, Find_(T, y) -> left -> DATA, Find_(T, y) -> right -> DATA, Find_(T, y) -> parent -> right -> DATA);

    else if((Find_(T, y) -> left == NULL || Find_(T, y) -> right == NULL) && (Find_(T, y) -> parent -> left == NULL || Find_(T, y) -> parent -> right == NULL))        // 缺少左孩子+左兄弟 或者 缺少右孩子+右兄弟的中间节点的中间节点

    {

        if(Find_(T, y) -> left == NULL && Find_(T, y) -> parent -> left == NULL)

            printf("\n%d 的双亲为:%d 无左孩子 右孩子为:%d 无左兄弟 右兄弟为自己本身: %d\n", Find_(T, y) -> DATA, Find_(T, y) -> parent -> DATA, Find_(T, y) -> right -> DATA, Find_(T, y) -> parent -> right -> DATA);

        else

            printf("\n%d 的双亲为:%d 左孩子为:%d 无右孩子 左兄弟为自己本身: %d 无右兄弟\n", Find_(T, y) -> DATA, Find_(T, y) -> parent -> DATA, Find_(T, y) -> left -> DATA, Find_(T, y) -> parent -> left -> DATA);

    }

    else                    // 健全的中间节点

        printf("\n%d 的双亲为:%d 左孩子为:%d 右孩子为:%d 左兄弟%s:%d 右兄弟%s:%d\n", Find_(T, y) -> DATA, Find_(T, y) -> parent -> DATA, Find_(T, y) -> left -> DATA, Find_(T, y) -> right -> DATA, (y == Find_(T, y) -> parent -> left -> DATA ? "为自己本身" : " "), Find_(T, y) -> parent -> left -> DATA, (y == Find_(T, y) -> parent -> right -> DATA ? "为自己本身" : " "), Find_(T, y) -> parent -> right -> DATA);

}

　　二叉树总结：

　　二叉树是一种每个节点至多有两个子节点的具有一对多的数据关系的数据结构。如果每个根节点都具有两个子节点，我们便将这种二叉树叫做“满二叉树”；如果每个节点都是连续的，我们便将这种二叉树称作“完全二叉树”，所以“满二叉树”一定是“完全二叉树”，但完全二叉树不一定是满二叉树；还有“斜树”这种特殊的二叉树，顾名思义，这种树要么线性的左斜，要么线性的右斜，每个节点只有一个子节点，具有前驱后继的线性关系，故而单链表就是二叉树的特殊情况。还有一种二叉树叫做线索二叉树，运用其中的技术可以将一个二叉树转换为一个双向链表（膜拜前人...）。

　　哈夫曼树也是一种二叉树，它也很强大，它可以应用于实现对数据的压缩（哈夫曼编码），还可以运用哈夫曼树的知识找到一些实用的最优二叉树。

　　二叉树还可以与树之间相互转换，怎样判断二叉树转换成树之后是成为森林还是一个树就看根节点是否有右孩子。

----------------------Update 2017.9.14 13:12:30 ------------------------

　　这几天因为开学所以没怎么碰电脑，昨天才开始继续我的数据结构的学习，然后认真的分析了二叉树的删除操作...虽然独立写出完整的删除可能还是不行，但对它的理解有了新的想法，于是想把这个想法先记录下来。

　　二叉树的删除操作在我看过的书上分成两个不同的处理方法：

　　　　1.找到恰好比删除的节点数据大的节点；

　　　　2.找到恰好比删除的节点数据小的节点。

　　这两个对实际进行删除操作的代码的编写有些不同。

　　用图形可视化来解释最简单:

　　这是一个高度为3的满二叉树，进行删除时也是情况最复杂的一种，因为删除非叶节点时，所有的节点都有两个子节点。这里假设删除右子树中的数据为65的节点：

　　实际上按照上面说的两个不同的删除方式，它最终可以得到两种不同的二叉树：

　　　对应第一种情况为:

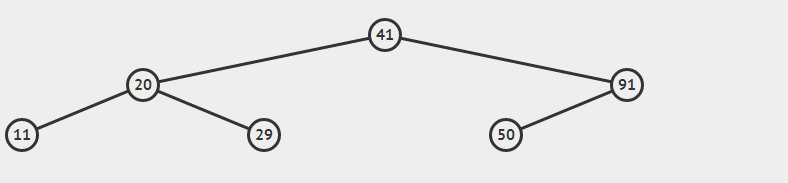
　　　　对应第二种情况为:

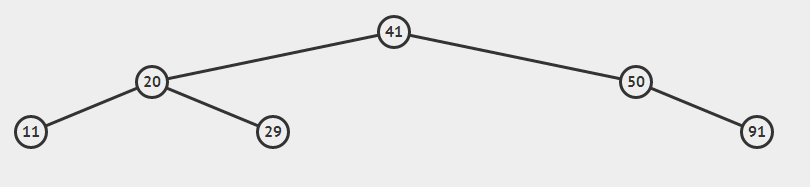
　　我来解释一下这里两种的不同情况的具体过程:

　　第一种情况：

　　　　因为编写代码的想法是先找到输入的数据对应的节点，然后判断该节点是否有子节点（无、一个或两个），无和有一个的情况很简单就不多说了，有两个子节点时，我们要在删除节点下去找到比删除节点大却又比右边的子节点都要小的节点（就是恰好比删除节点大的节点）并且找到的节点不能有左孩子（毕竟要比删除的节点大又要比其他节点小，所以最终一定会找到某个左节点身上），这样子再把删除节点的左孩子接到这个左节点的左边，把删除节点的右子树接到该左节点的右边，如果左节点有右孩子则把它接到左节点的父节点的左边。

　　　　如图（删除图中的65）：

　　　　　　按第一种情况就应该是找到69，把50接到69的左边，69有右孩子71，把71接到72左边，91接到69的右边,69接到41的右边就完成了

　　　　删除后得到的二叉树是这样的：

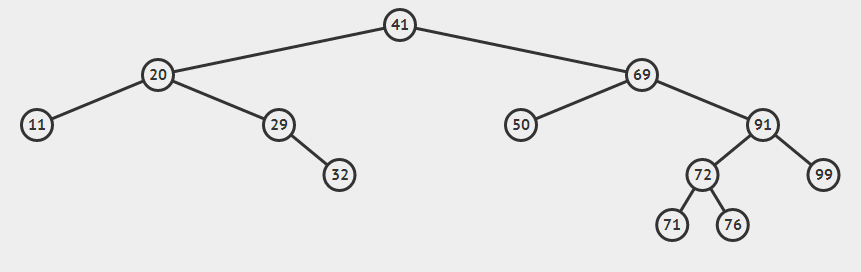
　　　第二种情况：

　　　　先找到输入的数据对应的节点，与第一种情况相反，编写一个函数来找比要删除的节点小但又比其他左边的子节点都要大的节点（也就是我说的恰好比该节点要小的节点）并且找到的节点不能有右孩子（因为有右孩子说明肯定比找到的节点要大一点），然后的操作就和第一种情况就差不多。

　　　　如图1（删除节点65）：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　图一

　　　　　　　　　　　　　　按第二种情况先找到恰比65小的节点50，把50接到41右边，91接到50右边就完成了

　　　　删除后的二叉树是这样的：

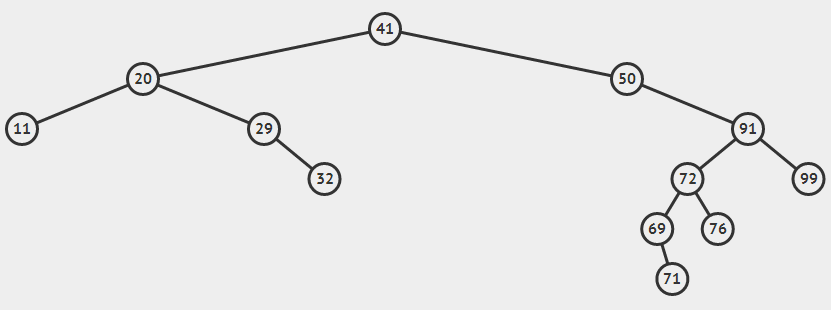
　　　　图一情况简单，再举例看看复杂点的，如图二（删除节点65）：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　图二

　　　　　按第二种情况先找到恰比65小的55，把55接到41右边，55有左孩子53，将53接到50右边，50接到55的左边，91接到55右边就完成了

　　　最后得到的二叉树就是这样的：

　　好了，我的想法就是这样，因为没有看到有人提到这两种不同的删除方式（也可能是我没认真看书，貌似《数据结构与算法分析》上有提到，我嫌字太多，没认真读...后来认真看了以后发现在习题里确实有说这两种不同的实现方法）加上最近对二叉树有怨念，就认真的分析了一下删除过程，然后发现其实不一定非要按第一种删除来编写代码，虽然我还是不会写删除，但也算是对它的理解更进一步了。

----------------Update 2017 9.16 17:06:26------------------

　　总算解决了个人对二叉树的学习，比较完整的解释请点击这里。

----------------Update 2017 9.20 12:57:04------------------

　　补充一段我理解的删除节点的第二种情况中找恰比删除节点小的节点的代码：

#include<stdio.h>

#include<stdlib.h>

#include<conio.h>

typedef int ElemType;

typedef struct tree {

    ElemType val;

    struct tree * left;

    struct tree * right;

    struct tree * parent;

}BiTree, * Tree;

BiTree * initBiTree();

static BiTree * MallocNode();

static BiTree * InsertNodePos();

BiTree * InsertNode();

static BiTree * Find();

static BiTree * FindDelNode_Min();

static void SubtreeChange();

static BiTree * DeleteNode();

BiTree * removeNode();

void In_Onder_Traverse();

BiTree * initBiTree(void)

{

    Tree root;

    root = NULL;

    return root;

}

static BiTree * MallocNode(Tree root, ElemType X)

{

    Tree newNode;

    newNode = (struct tree *)malloc(sizeof(struct tree));

    newNode -> val = X;

    newNode -> parent = newNode -> left = newNode -> right = NULL;

    return newNode;

}

static BiTree * InsertNodePos(Tree root, Tree newNode)

{

    Tree p, q;

    q = NULL;

    p = root;

    while(p != NULL)

    {

        q = p;

        if(newNode -> val < p -> val)

            p = p -> left;

        else if(newNode -> val > p -> val)

            p = p -> right;

        else

            break;

    }

    newNode -> parent = q;

    if(q == NULL)

        root = newNode;

    else if(newNode -> val < q -> val)

        q -> left = newNode;

    else

        q -> right = newNode;

    return root;

}

BiTree * InsertNode(Tree root, ElemType X)

{

    Tree newNode;

    if((newNode = MallocNode(root, X)) == NULL)

        return root;

    return InsertNodePos(root, newNode);

}

static BiTree * Find(Tree root, ElemType X)

{

    if(root == NULL)

        return root;

    else if(X < root -> val)

        return Find(root -> left, X);

    else if(X > root -> val)

        return Find(root -> right, X);

    else

        return root;

}

static BiTree * FindDelNode_Min(Tree root)        //找最大值节点。此处用来寻找恰比删除节点小的最大节点

{

    if(root == NULL)

        return NULL;

    else if(root -> right == NULL)

        return root;

    else

        return FindDelNode_Min(root -> right);

}

static void SubtreeChange(Tree root, Tree tempNode, Tree contNode)

{

    if(tempNode -> parent == NULL)

        root = contNode;

    else if(tempNode -> parent -> left == tempNode)

        tempNode -> parent -> left = contNode;

    else

        tempNode -> parent -> right = contNode;

    if(contNode != NULL)

        contNode -> parent = tempNode -> parent;

}

static BiTree * DeleteNode(Tree root, Tree delNode)

{

    Tree tempNode;

    if(delNode -> left == NULL)

        SubtreeChange(root, delNode, delNode -> right);

    else if(delNode -> left == NULL)

        SubtreeChange(root, delNode, delNode -> left);

    else

    {

        tempNode = FindDelNode_Min(delNode -> left);    //这里往该节点的左子树中查找即可找到该节点左子树中最大的节点

        if(tempNode -> parent != delNode)

        {

            SubtreeChange(root, tempNode, tempNode -> left);

            tempNode -> left = delNode -> left;

            tempNode -> left -> parent = tempNode;

        }

        SubtreeChange(root, delNode, tempNode);

        tempNode -> right = delNode -> right;

        tempNode -> right -> parent = tempNode;

    }

    free(delNode);

    return root;

}

BiTree * removeNode(Tree root, ElemType X)

{

    Tree delNode;

    if((delNode = Find(root, X)) == NULL)

        return root;

    return DeleteNode(root, delNode);

}

void In_Onder_Traverse(Tree root)

{

    if(root != NULL)

    {

        In_Onder_Traverse(root -> left);

        printf("%d ", root -> val);

        In_Onder_Traverse(root -> right);

    }

}

int main()

{

    Tree T;

    ElemType X;

    char c;

    T = initBiTree();

    puts("1) Add        2) Display");

    puts("3) Delete     4) Exit");

    while((c = getch()) != '4')

    {

        if(c == '1')

        {

            printf("Add:");

            scanf("%d", &X);

            T = InsertNode(T, X);

        }

        if(c == '2')

        {

            printf("Display:\n");

            In_Onder_Traverse(T);

        }

        if(c == '3')

        {

            printf("Delete:");

            scanf("%d", &X);

            removeNode(T, X);

        }

    }

    return 0;

}

　　至于第一种情况的代码就在上面 9.16的更新中给出的链接里面，所以就不重复了。

BinaryTree(二叉树)的更多相关文章

[BinaryTree] 二叉树类的实现
二叉树结点的抽象数据类型: template<class T> class BinaryTreeNode { friend class BinaryTree<T>; priva ...
[BinaryTree] 二叉树常考知识点
1.二叉树第i层至多有2^(i-1)个结点(i>=1). 2.深度为k的二叉树上,至多含2^k-1个结点(k>=1) 3.n0 = n2 + 1(度) 4.满二叉树:深度为k且含有2^k- ...
BinaryTree(二叉树) - 再谈二叉树
经过两天的研究,总算是完全梳理清二叉树的基本操作了,然后我又发现了一些对二叉树的新的认识. 先具体说说删除操作,前面在对二叉树的补充中,我说到了二叉树的删除操作可以有两种不同的代码编写方式(可点这里去 ...
二叉树JAVA实现
为了克服对树结构编程的畏惧感和神秘感,下定决心将二叉树的大部分操作实现一遍,并希望能够掌握二叉树编程的一些常用技术和技巧.关于编程实现中的心得和总结,敬请期待!~ [1] 数据结构和表示: 二叉树的 ...
数据结构与算法系列研究五——树、二叉树、三叉树、平衡排序二叉树AVL
树.二叉树.三叉树.平衡排序二叉树AVL 一.树的定义树是计算机算法最重要的非线性结构.树中每个数据元素至多有一个直接前驱,但可以有多个直接后继.树是一种以分支关系定义的层次结构. a.树是n ...
Python实现二叉树及其4种遍历
Python & BinaryTree 1. BinaryTree (二叉树) 二叉树是有限个元素的集合,该集合或者为空.或者有一个称为根节点(root)的元素及两个互不相交的.分别被称为左子 ...
C++实现二叉树的基本操作：建立、遍历、计算深度、节点数、叶子数等
题意: 代码实现: #include<iostream> #include<queue> #include<stack> using namespace std; ...
computer English
算法常用术语中英对照Data Structures 基本数据结构Dictionaries 字典PriorityQueues 堆Graph Data Structures 图Set Data Struc ...
给jdk写注释系列之jdk1.6容器(7)-TreeMap源码解析
TreeMap是基于红黑树结构实现的一种Map,要分析TreeMap的实现首先就要对红黑树有所了解. 要了解什么是红黑树,就要了解它的存在主要是为了解决什么问题,对比其他数据结构比如数组,链 ...

随机推荐

mongo日常命令集锦
查询某个字段是否存在 db.student.findOne({name:{$exists:true}}) db.student.findOne({'department.name':{$exists: ...
HBase 启动后HMaster进程自动消失
原因分析 1.hadoop 与 hbase 版本不兼容,导致的异常. 2.log日志信息显示 org.apache.hadoop.hbase.TableExistsException: hbase:n ...
实战【docker 镜像制作与使用】
一.制作docker 镜像使用spring boot 构建一个简单的web 项目,返回 “Hello,World ”字符串,使用 Maven 打成 jar 包,使用的Linux 环境是 Centos ...
Android学习10
SharedPreferences 今天练习了利用SharedPreferences保存登录用户名密码: layout布局: <?xml version="1.0" enco ...
Day0 认识Java与变量类型
字节码与虚拟机 Java介于编译型语言和解释型语言之间.编译型语言如C.C++,代码是直接编译成机器码执行,但是不同的平台(x86.ARM等)CPU的指令集不同,因此,需要编译出每一种平台的对应机器码 ...
BFSDFS模板
BFS模板: private static void bfs(HashMap<Character, LinkedList<Character>> graph,HashMap&l ...
cookie的封装
今天逛论坛,看到一个看起来写得好的函数,特此贴出分享: 原文地址[http://www.html-js.com/article/2638 ] 这个地址[https://github.com/jaywc ...
C：字符数组与字符串
字符串与字符数组 C语言中没有字符串这种数据类型,可以通过char的数组来替代: 字符串一定是一个char的数组,但char的数组未必是字符串: 数字0(和字符'\0'等价)结尾的char数组就是一个 ...
[Python] [转] python.exe和pythonw.exe的区别（区分.py、.pyw、.pyc文件）
Windows系统搭建好Python的环境后,进入Python的安装目录,大家会发现目录中有python.exe和pythonw.exe两个程序.如下图所示: 它们到底有什么区别和联系呢? 概括说明一 ...
JavaScript 对象的深复制
对象的深复制源对象的属性更改,不会引起复制后的对象个属性的更改源对象的任何属性与子属性与新对象的之间没有任何引用关系 Coding: /* 对象的深复制: 1 初始化目标对象如果没有指定目标对象 ...

BinaryTree(二叉树)

BinaryTree(二叉树)的更多相关文章

随机推荐

热门专题