LeetCode——230. 二叉搜索树中第K小的元素

给定一个二叉搜索树，编写一个函数 kthSmallest 来查找其中第 k 个最小的元素。

说明：

你可以假设 k 总是有效的，1 ≤ k ≤ 二叉搜索树元素个数。

示例 1:

输入: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
输出: 1

示例 2:

输入: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
输出: 3

进阶：

如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化 kthSmallest 函数？

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/kth-smallest-element-in-a-bst

一

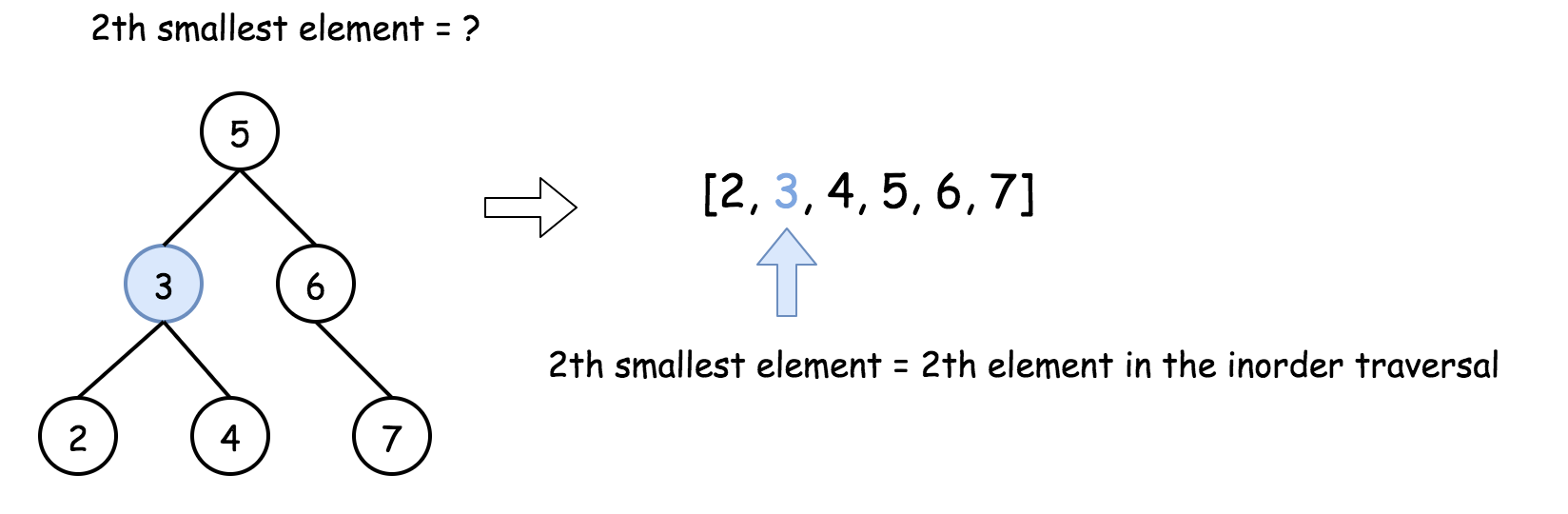
为了解决这个问题，可以使用 BST 的特性：BST 的中序遍历是升序序列。

方法一：递归

算法：

通过构造 BST 的中序遍历序列，则第 k-1 个元素就是第 k 小的元素。

Python

class Solution:
    def kthSmallest(self, root, k):
        def inorder(r):
            return inorder(r.left) + [r.val] + inorder(r.right) if r else []

        return inorder(root)[k - 1]

java

class Solution {
  public ArrayList<Integer> inorder(TreeNode root, ArrayList<Integer> arr) {
    if (root == null) return arr;
    inorder(root.left, arr);
    arr.add(root.val);
    inorder(root.right, arr);
    return arr;
  }

  public int kthSmallest(TreeNode root, int k) {
    ArrayList<Integer> nums = inorder(root, new ArrayList<Integer>());
    return nums.get(k - 1);
  }
}

复杂度分析

时间复杂度：O(N)，遍历了整个树。

空间复杂度：O(N)，用了一个数组存储中序序列。

方法二：迭代

算法：

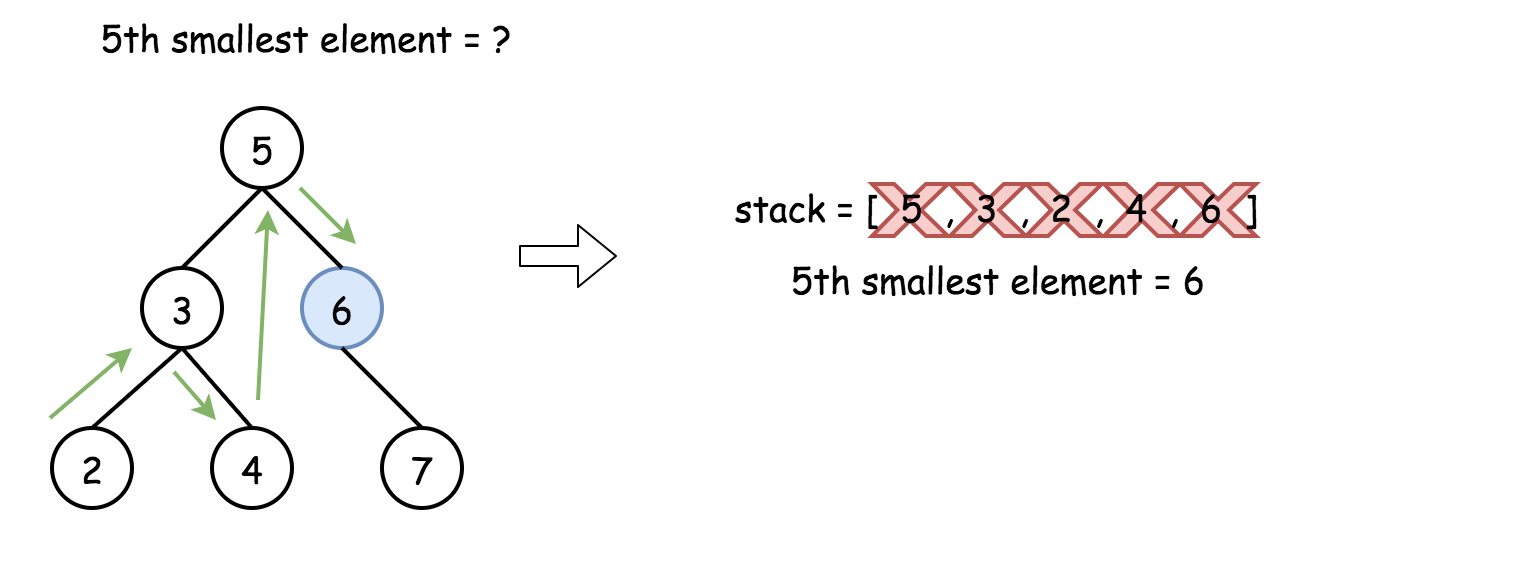
在栈的帮助下，可以将方法一的递归转换为迭代，这样可以加快速度，因为这样可以不用遍历整个树，可以在找到答案后停止。

Python

class Solution:
    def kthSmallest(self, root, k):
        stack = []

        while True:
            while root:
                stack.append(root)
                root = root.left
            root = stack.pop()
            k -= 1
            if not k:
                return root.val
            root = root.right

java

class Solution {
  public int kthSmallest(TreeNode root, int k) {
    LinkedList<TreeNode> stack = new LinkedList<TreeNode>();

    while (true) {
      while (root != null) {
        stack.add(root);
        root = root.left;
      }
      root = stack.removeLast();
      if (--k == 0) return root.val;
      root = root.right;
    }
  }
}

复杂度分析

时间复杂度：O(H+k)，其中 HH 指的是树的高度，由于我们开始遍历之前，要先向下达到叶，当树是一个平衡树时：复杂度为 O(logN+k)。当树是一个不平衡树时：复杂度为 O(N+k)，此时所有的节点都在左子树。

空间复杂度：O(H+k)。当树是一个平衡树时：O(logN+k)。当树是一个非平衡树时：O(N+k)。

二

LeetCode 中关于 BST 的题有 [Validate Binary Search Tree]， [Recover Binary Search Tree]， [Binary Search Tree Iterator]， [Unique Binary Search Trees]， [Unique Binary Search Trees II]，[Convert Sorted Array to Binary Search Tree] 和 [Convert Sorted List to Binary Search Tree]。那么这道题给的提示是让我们用 BST 的性质来解题，最重要的性质是就是左<根<右，如果用中序遍历所有的节点就会得到一个有序数组。所以解题的关键还是中序遍历啊。先来看一种非递归的方法，中序遍历最先遍历到的是最小的结点，只要用一个计数器，每遍历一个结点，计数器自增1，当计数器到达k时，返回当前结点值即可，参见代码如下：

解法一：

class Solution {
public:
    int kthSmallest(TreeNode* root, int k) {
        int cnt = 0;
        stack<TreeNode*> s;
        TreeNode *p = root;
        while (p || !s.empty()) {
            while (p) {
                s.push(p);
                p = p->left;
            }
            p = s.top(); s.pop();
            ++cnt;
            if (cnt == k) return p->val;
            p = p->right;
        }
        return 0;
    }
};

当然，此题我们也可以用递归来解，还是利用中序遍历来解，代码如下：

解法二：

class Solution {
public:
    int kthSmallest(TreeNode* root, int k) {
        return kthSmallestDFS(root, k);
    }
    int kthSmallestDFS(TreeNode* root, int &k) {
        if (!root) return -1;
        int val = kthSmallestDFS(root->left, k);
        if (k == 0) return val;
        if (--k == 0) return root->val;
        return kthSmallestDFS(root->right, k);
    }
};

再来看一种分治法的思路，由于 BST 的性质，可以快速定位出第k小的元素是在左子树还是右子树，首先计算出左子树的结点个数总和 cnt，如果k小于等于左子树结点总和 cnt，说明第k小的元素在左子树中，直接对左子结点调用递归即可。如果k大于 cnt+1，说明目标值在右子树中，对右子结点调用递归函数，注意此时的k应为 k-cnt-1，应为已经减少了 cnt+1 个结点。如果k正好等于 cnt+1，说明当前结点即为所求，返回当前结点值即可，参见代码如下：

解法三：

class Solution {
public:
    int kthSmallest(TreeNode* root, int k) {
        int cnt = count(root->left);
        if (k <= cnt) {
            return kthSmallest(root->left, k);
        } else if (k > cnt + 1) {
            return kthSmallest(root->right, k - cnt - 1);
        }
        return root->val;
    }
    int count(TreeNode* node) {
        if (!node) return 0;
        return 1 + count(node->left) + count(node->right);
    }
};

这道题的 Follow up 中说假设该 BST 被修改的很频繁，而且查找第k小元素的操作也很频繁，问我们如何优化。其实最好的方法还是像上面的解法那样利用分治法来快速定位目标所在的位置，但是每个递归都遍历左子树所有结点来计算个数的操作并不高效，所以应该修改原树结点的结构，使其保存包括当前结点和其左右子树所有结点的个数，这样就可以快速得到任何左子树结点总数来快速定位目标值了。定义了新结点结构体，然后就要生成新树，还是用递归的方法生成新树，注意生成的结点的 count 值要累加其左右子结点的 count 值。然后在求第k小元素的函数中，先生成新的树，然后调用递归函数。在递归函数中，不能直接访问左子结点的 count 值，因为左子节结点不一定存在，所以要先判断，如果左子结点存在的话，那么跟上面解法的操作相同。如果不存在的话，当此时k为1的时候，直接返回当前结点值，否则就对右子结点调用递归函数，k自减1，参见代码如下：

解法四：

// Follow up
class Solution {
public:
    struct MyTreeNode {
        int val;
        int count;
        MyTreeNode *left;
        MyTreeNode *right;
        MyTreeNode(int x) : val(x), count(1), left(NULL), right(NULL) {}
    };

    MyTreeNode* build(TreeNode* root) {
        if (!root) return NULL;
        MyTreeNode *node = new MyTreeNode(root->val);
        node->left = build(root->left);
        node->right = build(root->right);
        if (node->left) node->count += node->left->count;
        if (node->right) node->count += node->right->count;
        return node;
    }

    int kthSmallest(TreeNode* root, int k) {
        MyTreeNode *node = build(root);
        return helper(node, k);
    }

    int helper(MyTreeNode* node, int k) {
        if (node->left) {
            int cnt = node->left->count;
            if (k <= cnt) {
                return helper(node->left, k);
            } else if (k > cnt + 1) {
                return helper(node->right, k - 1 - cnt);
            }
            return node->val;
        } else {
            if (k == 1) return node->val;
            return helper(node->right, k - 1);
        }
    }
};