Cracking Digital VLSI Verification Interview 第一章

欢迎关注个人公众号摸鱼范式

目录

• Digital Logic Design
  • Number Systems, Arithmetic and Codes
    • [1] 将下列十进制数转换为有符号二进制，八进制和十六进制，使用尽可能少的比特位
    • [2] 0x3A的十进制数是多少？
    • [3] 什么是格雷码，格雷码相对于普通二进制码有什么好处？
    • [4] 什么是奇偶校验位，如何计算？
    • [5] 计算二进制数111001的奇校验位
    • [6] 什么是BCD码，他和二进制码有什么区别？十进制27的二进制码和BCD码是什么？
  • Basic Gates
    • [7] 以下哪个是通用门？为什么？
    • [8] 如何使用两个两输入与非门实现，两输入与门，两输入或门，非门？
    • [9] 如何使用两个两输入或非门实现，两输入与门，两输入或门，非门？
    • [10] 用一个2:1MUX构成下面的门
    • [11] 异或门在数据通信中的典型应用是什么？
    • [12] 三输入与非门的输出何时为0？
    • [13] 如何使用异或门实现一个非门
  • Combinational Logic Circuits
    • [14] 请用2:1选择器实现4:1选择器
    • [15] 什么是环形振荡器？如果每个门的延迟是2ps，使用三个非门的环形振荡器的频率是什么？
  • Sequential Circuits and State Machines
    • [16] 同步电路和异步电路有什么不同？
    • [17] 阐述建立时间和保持时间
    • [18] 解释什么是clock skew
    • [19] 下图output delay为10ns，setup time为5ns，hold time为2ns，组合逻辑delay为10ns，请计算该电路的最大工作频率
    • [20] 触发器和锁存器的区别什么？
    • [21] 什么是竞争？什么时候会出现？如何避免？
    • [22] 用2:1mux实现D触发器
    • [23] 用D触发器实现T触发器
    • [24] 用JK触发器实现D触发器
    • [25] 行波进位加法器和超前进位加法器的区别是？
    • [26] 实现一个32bit寄存器需要几个flip-flop？
    • [27] mealy型FSM和moore型FSM有什么区别？
    • [28] 九个状态的记录最少需要几个FF？
    • [29] 使用尽可能少的DFF实现二分频和四分频

对Cracking Digital VLSI Verification Interview：Interview Success这本书的汉化，最新更新请关注微信公众号 摸鱼范式

Digital Logic Design

Number Systems, Arithmetic and Codes

[1] 将下列十进制数转换为有符号二进制，八进制和十六进制，使用尽可能少的比特位

a)17

b)-17

a: 对17辗转相除，得到其二进制为010001，八进制为21，十六进制为0x11。注意二进制必须是010001，而不是10001，不能缺少符号位

b: 根据17的二进制，-17的二进制数原码位110001，取反加一得到补码为101111，因此八进制为57，十六进制为0x2f

二进制转八进制，取三合一，二进制转十六进制，取四合一

[2] 0x3A的十进制数是多少？

ans=3*16^1+10*160=58

[3] 什么是格雷码，格雷码相对于普通二进制码有什么好处？

格雷码是一种二值编码，相邻的编码之间只有一位的区别。因此与普通二进制码相比，在递增时出错概率更加小。下表是3bit的格雷码编码：

十进制	二进制	格雷码
0	000	000
1	001	001
2	010	011
3	011	010
4	100	110
5	101	111
6	110	101
7	111	100

此外，由于格雷码中比特位变化比较少，与二进制码相比，使用格雷码的功耗更加低

[4] 什么是奇偶校验位，如何计算？

奇偶校验位是在一串二进制码的最后添加的一位，它使得整个二进制串的1的个数为奇数或者偶数。因此奇偶校验分为两种，奇校验和偶校验。

计算校验位需要对二进制码中的1进行计数。如果1的数量为奇数，并且使用偶校验，则校验位为1，使得整体1的个数为偶数。如果1的数量为偶数，并且使用偶校验，则校验位为0，使得整体1的个数为偶数。奇校验类似。奇偶校验位可以通过对所有的比特位进行异或得到。

[5] 计算二进制数111001的奇校验位

111001中1的个数为4个，所以校验位为1，带上校验位以后为1110011，1的个数为5，为奇数

[6] 什么是BCD码，他和二进制码有什么区别？十进制27的二进制码和BCD码是什么？

BCD码也称二进码十进数，BCD码可分为有权码和无权码两类。其中，常见的有权BCD码有8421码、2421码、5421码，无权BCD码有余3码、余3循环码、格雷码。8421BCD码是最基本和最常用的BCD码，它和四位自然二进制码相似，各位的权值为8、4、2、1，故称为有权BCD码。

2的二进制位0010，7的二进制位0111，十进制27的8421BCD码为，00100111，二进制码为11011

Basic Gates

[7] 以下哪个是通用门？为什么？

• AND
• NAND
• OR
• NOR
• XOR

通用门是可以实现任何布尔函数而无需使用任何其他门类型的门。 与非门或非门是通用门。

[8] 如何使用两个两输入与非门实现，两输入与门，两输入或门，非门？

与门：

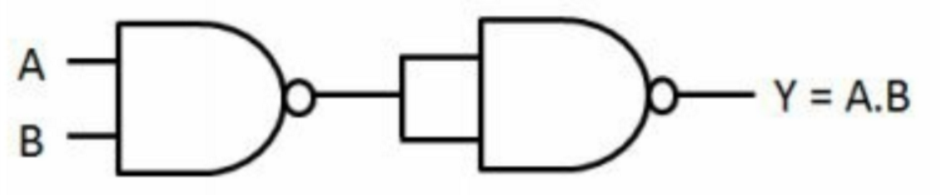
或门：

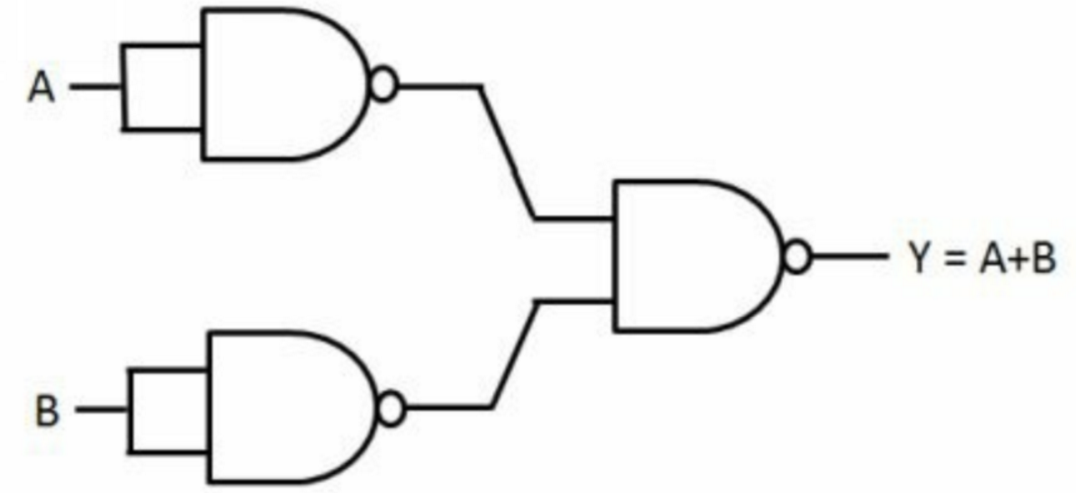
非门：

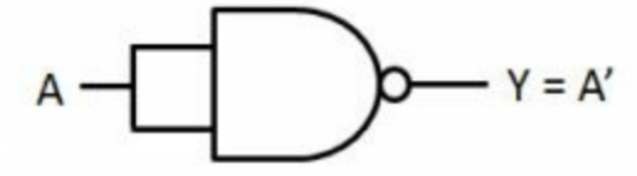
[9] 如何使用两个两输入或非门实现，两输入与门，两输入或门，非门？

与门：

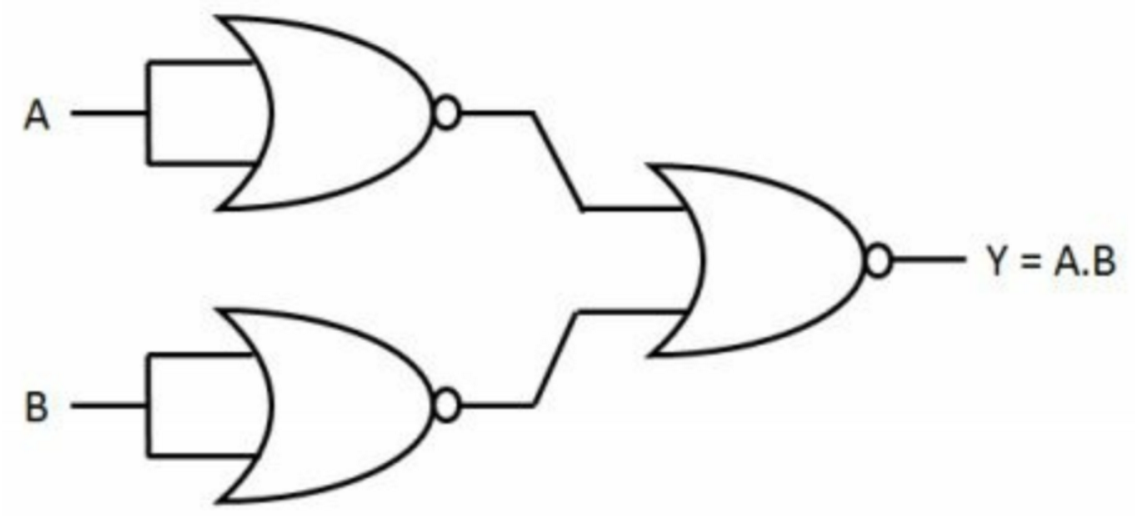
或门：

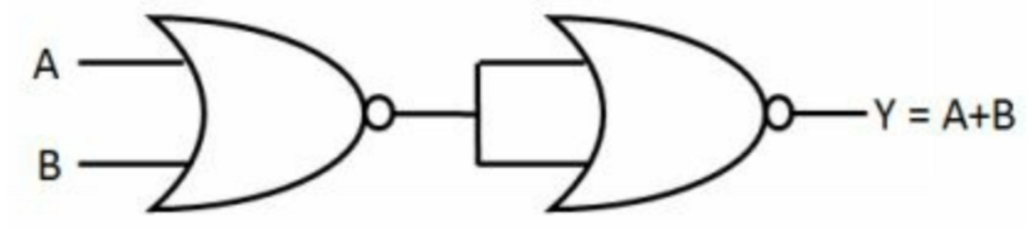
非门：

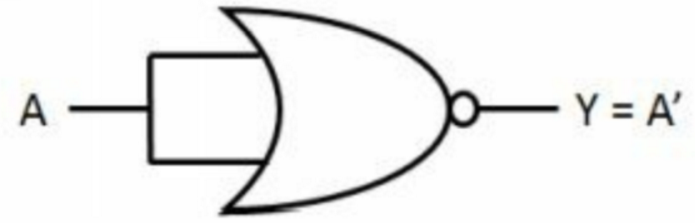
[10] 用一个2:1MUX构成下面的门

• 非门
• 两输入与门
• 两输入或门
• 两输入或非门
• 两输入与非门
• 两输入异或门

非门：

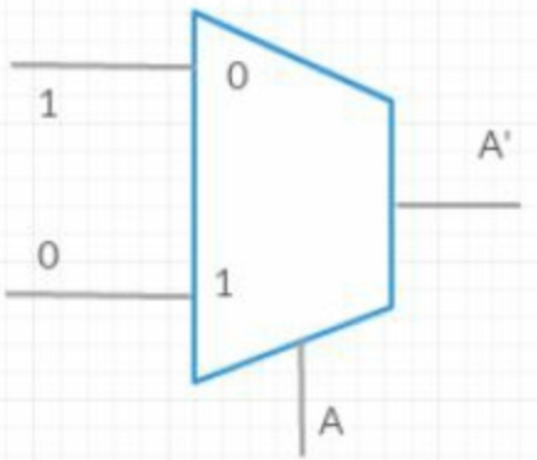
与门：

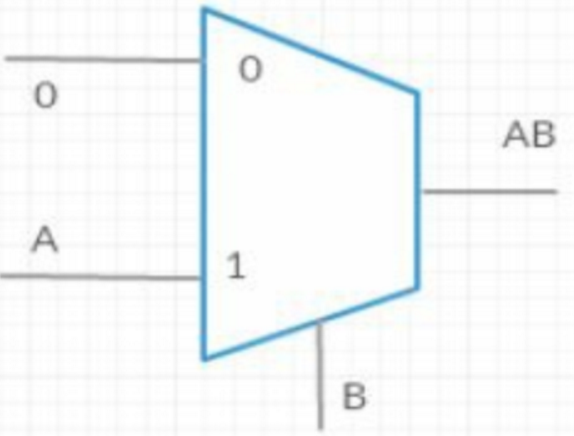
或门：

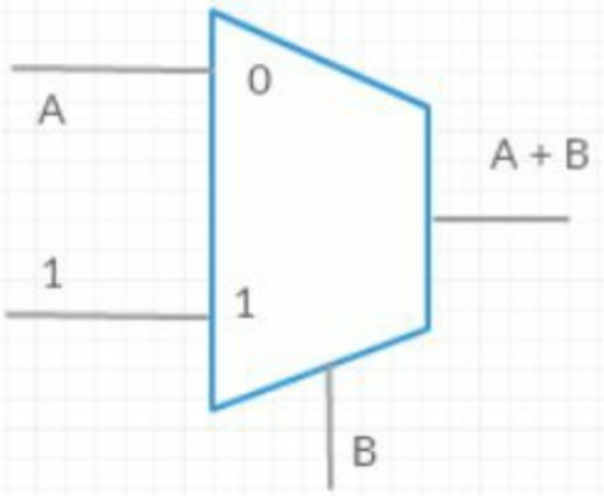
或非门：用或门和非门组成

与非门：用与门和非门组成

异或门：

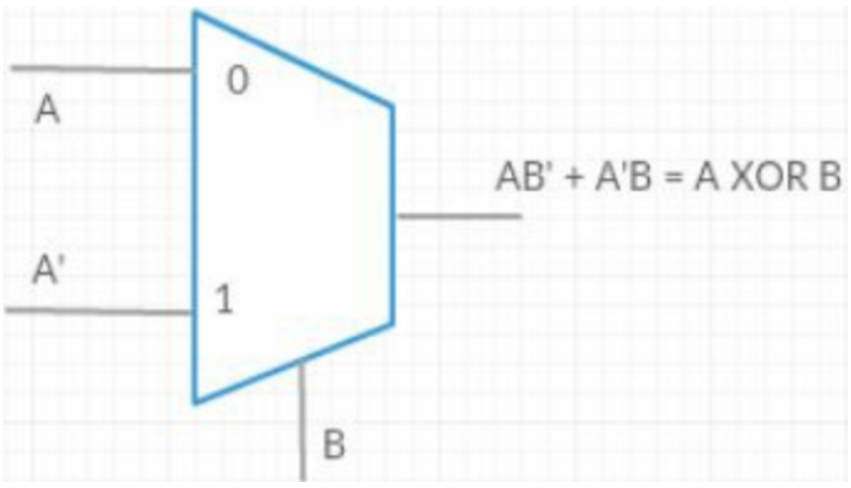
[11] 异或门在数据通信中的典型应用是什么？

通常被用于错误检测，例如，奇偶校验，CRC校验，ECC。异或门也可以用于伪随机数生成。

[12] 三输入与非门的输出何时为0？

所有输入都为1

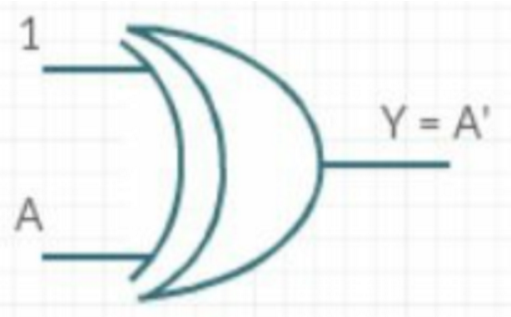
[13] 如何使用异或门实现一个非门

Combinational Logic Circuits

[14] 请用2:1选择器实现4:1选择器

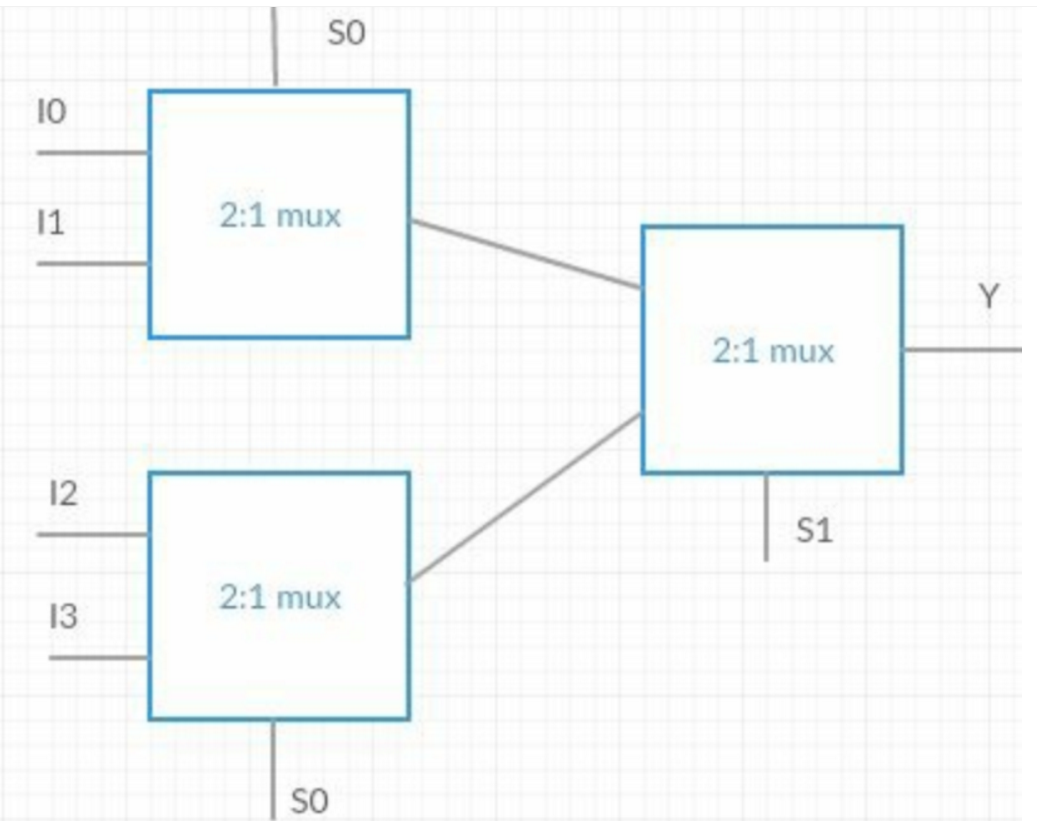
[15] 什么是环形振荡器？如果每个门的延迟是2ps，使用三个非门的环形振荡器的频率是什么？

环形振荡器可以由奇数个非门组成，非门或者反相器连接成链后，最后一个输出反馈回第一个反相器。

三个反相器，信号需要经过两次反馈，即2*3个反相器，振荡频率为1/(6*2ps) = 1000/12 GHz = 83.33 GHz

Sequential Circuits and State Machines

[16] 同步电路和异步电路有什么不同？

时序电路分为两种，同步时序电路和异步时序电路

同步时序电路在适中的上升沿或者下降沿改变状态和输出值。常见的例子是flip-flop，在时钟边沿根据输入改变输出。

异步时序电路的状态和输出值是根据使能信号进行控制，这更加类似于一个带有反馈的组合逻辑。

[17] 阐述建立时间和保持时间

建立时间是在时钟进行有效转换前数据信号应该保持稳定的最短时间。

保持时间是在时钟进行有效转换后数据信号应该保持稳定的最短时间。

[18] 解释什么是clock skew

时钟信号到达两个FF的时间差称之为clock skew(时钟偏斜)

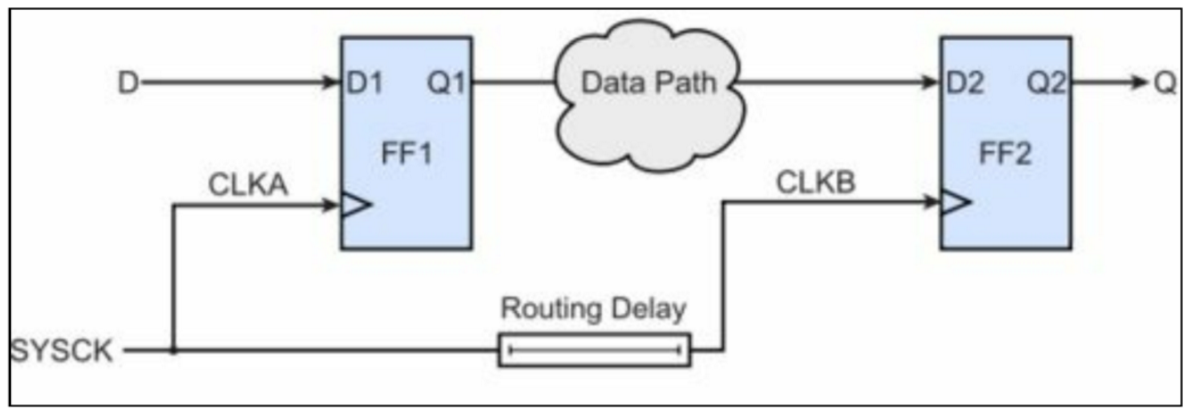
例如图中两个FF的时钟，虽然是同一个时钟源，但是由于走线的延迟，导致a的时钟比b的快。

[19] 下图output delay为10ns，setup time为5ns，hold time为2ns，组合逻辑delay为10ns，请计算该电路的最大工作频率

建立时间约束为\(t_{clk-q}+t_{plogic}+t_{setup}<=T\),即\(T>=25ns\)，最大工作频率为40Mhz

[20] 触发器和锁存器的区别什么？

触发器和锁存器都是存储信息的基本单元。一个触发器或者锁存器能够存储一bit的信息。两者的主要不同点是，触发器只在时钟上升沿或者下降沿根据采样改变输出，而锁存器在enable信号拉高期间都会跟随输入。

[21] 什么是竞争？什么时候会出现？如何避免？

当输出取决于不同信号的顺序或者时序时，被称为竞争。竞争可以分为两种

1. 实际的硬件中的竞争
2. 仿真行为中的竞争

实际硬件中的竞争：以SR锁存器为例，当SR都是1的时候，输出为1，此时如果SR同时变成0，那么Q和Q'就会进入竞争的情况。可以通过添加合适的逻辑避免。

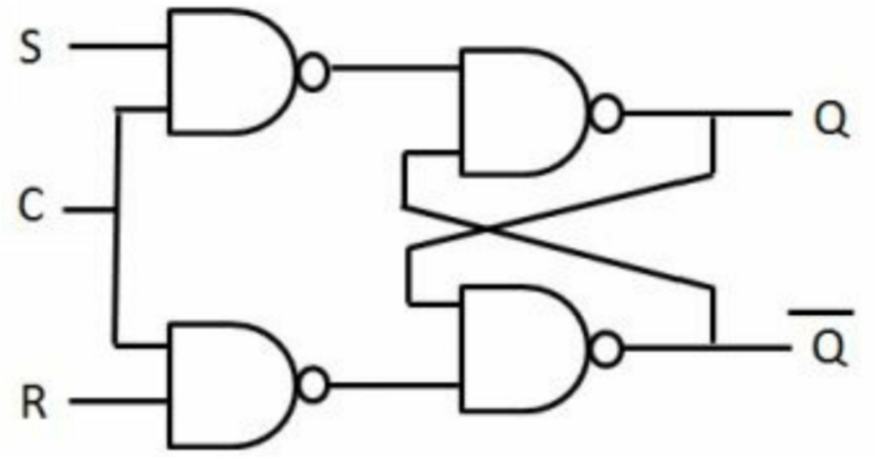
仿真行为中的竞争：例如下面的代码

always @(posedge clk or posedge reset)
    if (reset) X1 = 0; // reset
    else X1 = X2;
always @(posedge clk or posedge reset)
    if (reset) X2 = 1; // reset
    else X2 = X1;

由于使用了阻塞赋值，便会发生竞争的情况，通过改为非阻塞赋值可以解决

[22] 用2:1mux实现D触发器

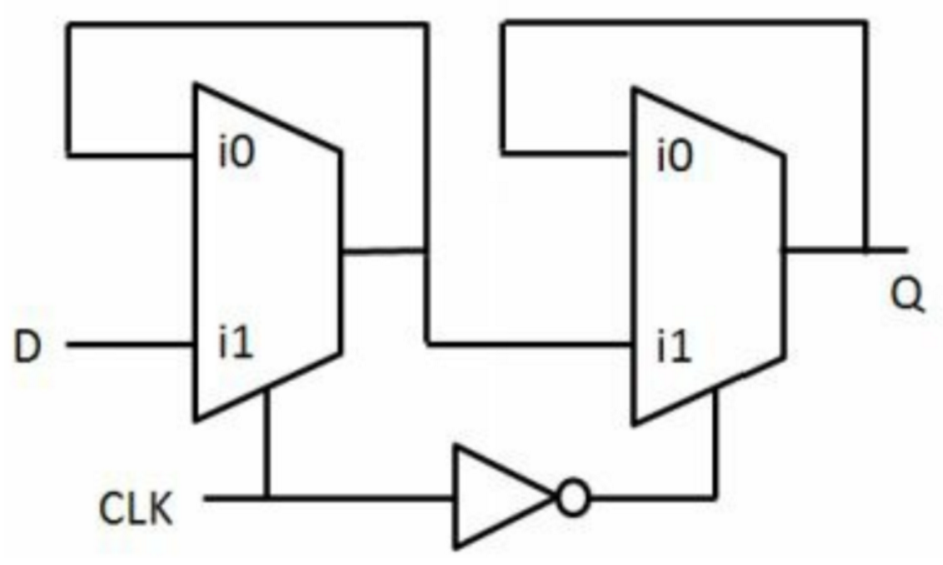
[23] 用D触发器实现T触发器

T触发器，T为0时输出不变，1时翻转。写出真值表就能看出来，将输入和Q异或再输入到D端。

[24] 用JK触发器实现D触发器

J=D，K=D'

[25] 行波进位加法器和超前进位加法器的区别是？

行波进位加法器：

结构类似于我们拿笔在纸上做加法的方法。从最低位开始做加法，将进位结果送到下一级做和。由于本级的求和需要等待前一级的进位结果才可以得到，所以对于两个N-bit的求和。即使有N个一位的全加器，也需要N个延迟。

超前进位加法器：

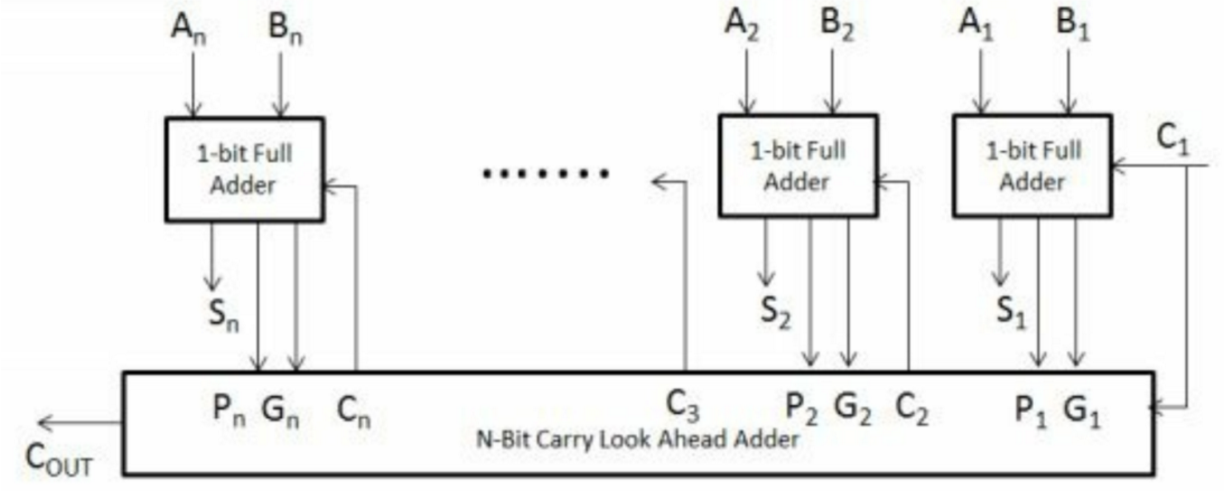
事实上，在以下两种情况中，Ci=1：

1. Ai和Bi都为1
2. Ai和Bi有一个为1，且Ci-1为1

其对应的表达式为

递归后

可以看出每一级的进位信号可以不通过上一级的结果产生，只与输入有关系。因此减少了时间。

[26] 实现一个32bit寄存器需要几个flip-flop？

一个FF存储一bit信息，因此需要32个FF。

[27] mealy型FSM和moore型FSM有什么区别？

mealy型FSM的输出和当前的状态以及当前的输入有关系。

moore型FSM的输出只和当前的状态有关系。

[28] 九个状态的记录最少需要几个FF？

2^3 < 9 < 2^4，因此是4个

[29] 使用尽可能少的DFF实现二分频和四分频

二分频：

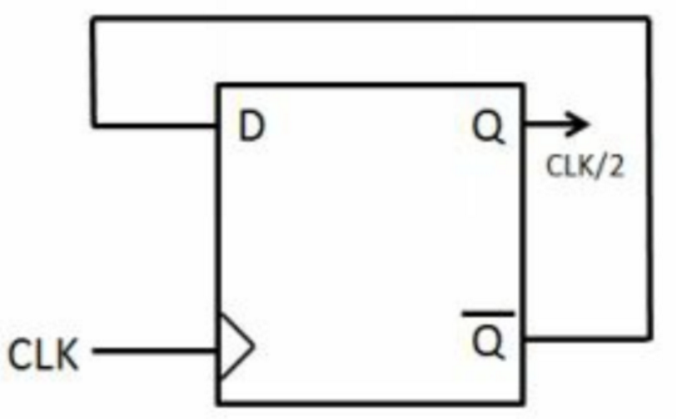
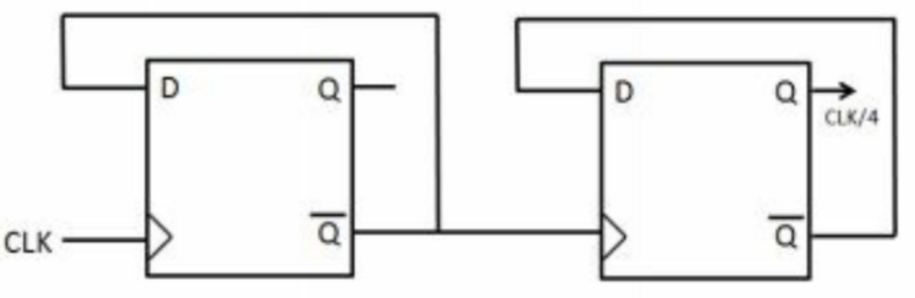
四分频：