K-means聚类分析

一、原理

1. 先确定簇的个数，K
2. 假设每个簇都有一个中心点 centroid
3. 将每个样本点划分到距离它最近的中心点所属的簇中

选择K个点做为初始的中心点
while（）
{
      将所有点分配个K个中心点形成K个簇
      重新计算每个簇的中心点
      if（簇的中心点不再改变）
break；
}

• 目标函数：定义为每个样本与其簇中心点的距离的 平方和（theSum of Squared Error, SSE）

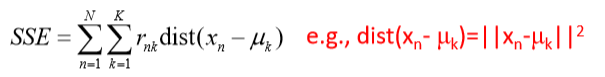
　　– μk 表示簇Ck 的中心点（或其它能代表Ck的点）

　　– 若xn被划分到簇Ck则rnk=1，否则rnk= 0

• 目标：找到簇的中心点μk及簇的划分rnk使得目标 函数SSE最小

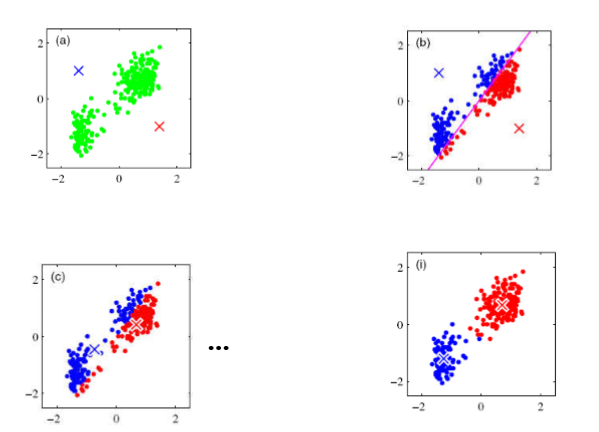
• 初始中心点通常是随机选取的（收敛后得到的是局部最优解）

不同的中心点会对聚类结果产生不同的影响：

1、

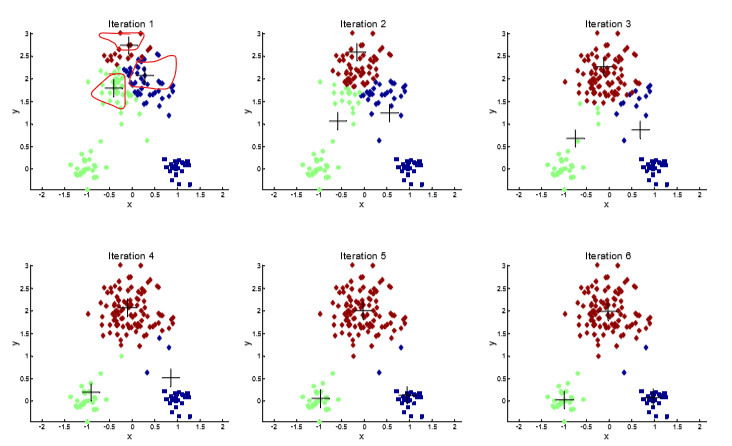
2、

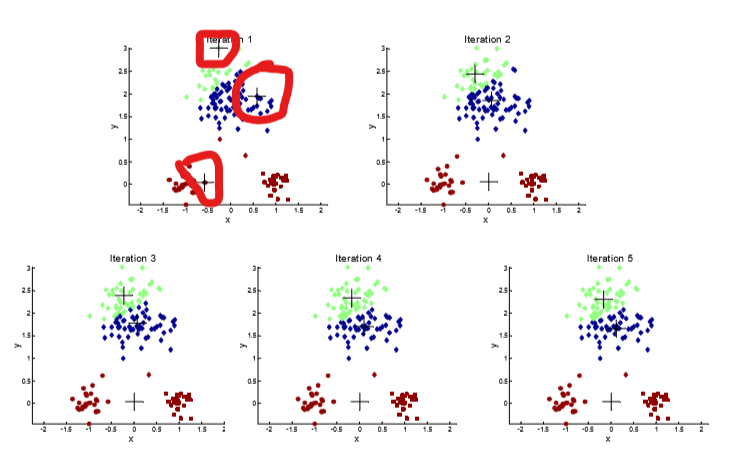
此时你一定会有疑问：如何选取"较好的"初始中心点？

1. 凭经验选取代表点
2. 将全部数据随机分成c类，计算每类重心座位初始点
3. 用“密度”法选择代表点
4. 将样本随机排序后使用前c个点作为代表点
5. 从(c-1)聚类划分问题的解中产生c聚类划分问题的代表点

　　　　结论：若对数据不够了解，可以直接选择2和4方法

• 需要预先确定K

　　　Q：如何选取K

　　SSE一般随着K的增大而减小

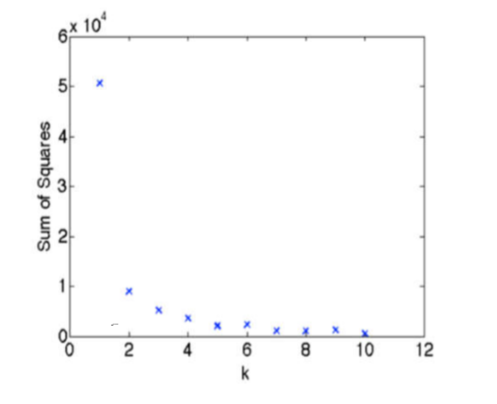
A：emmm你多尝试几次吧，看看哪个合适。斜率改变最大的点比如k=2

总结：

简单的来说，K-means就是假设有K个簇，然后通过上面找初始点的方法，找到K个初始点，将所有的数据分为K个簇，然后一直迭代，在所有的簇里面找到找到簇的中心点μk及簇的划分rnk使得目标函数SSE最小或者中心点不变之后，迭代完成。成功把数据分为K类。

预告：下一篇博文讲K-means代码实现