第11章 支撑向量机SVM
Support Vector Machine
 ,
,
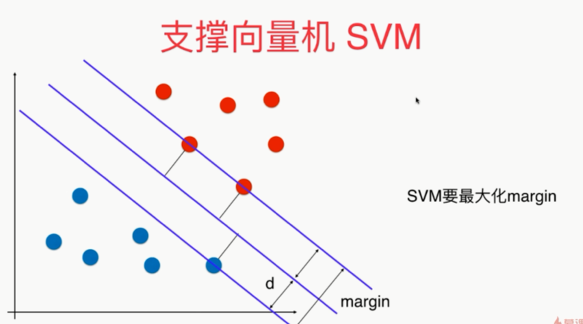
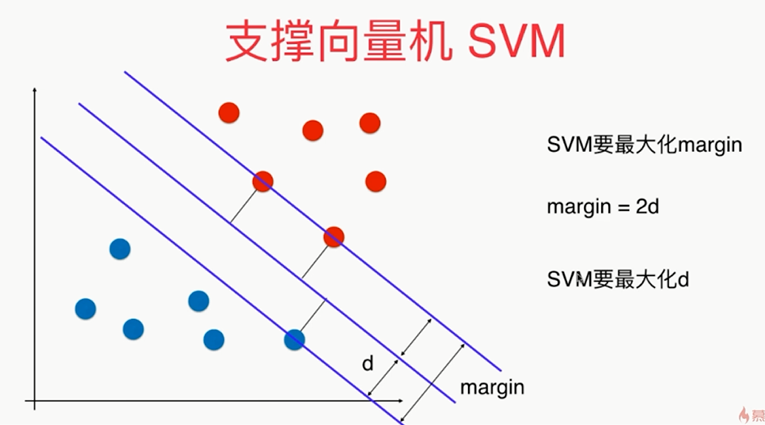
问题:如果决策边界不唯一
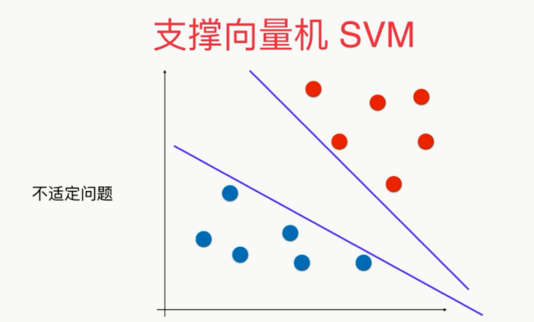 ,
,
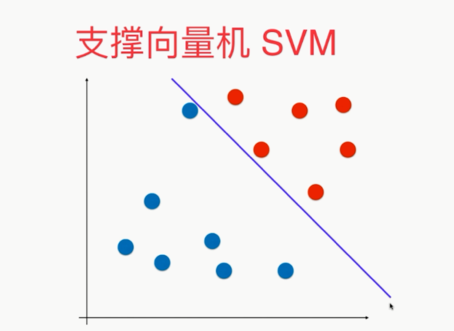 ,
,
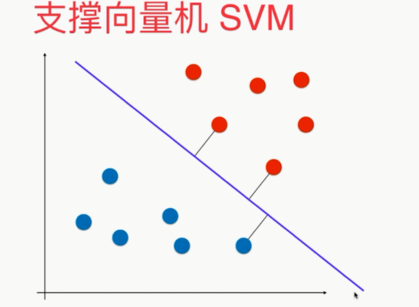 ,
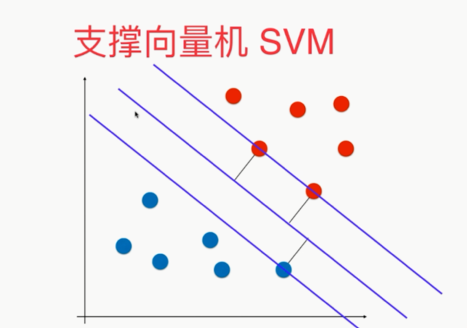
,
 ,
,
 ,
,
 ,
,
 ,
,
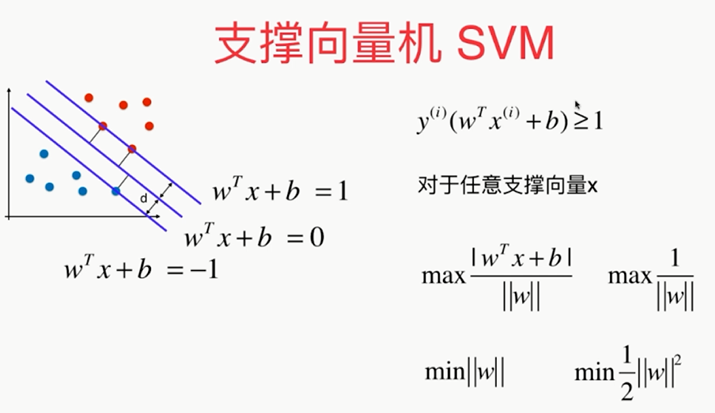 ,
,
s.t.(such that):之前都是全局最优化问题,这次是有条件的最优化问题
hard margin svm:首先保证能正确的分类
 ,
,
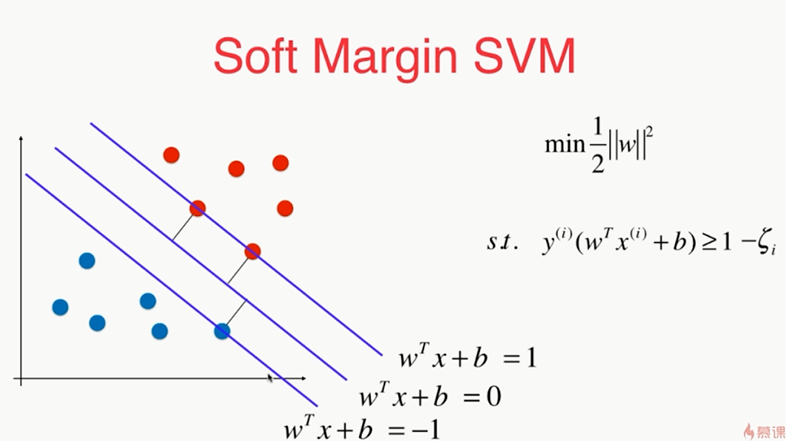
soft margin SVM:
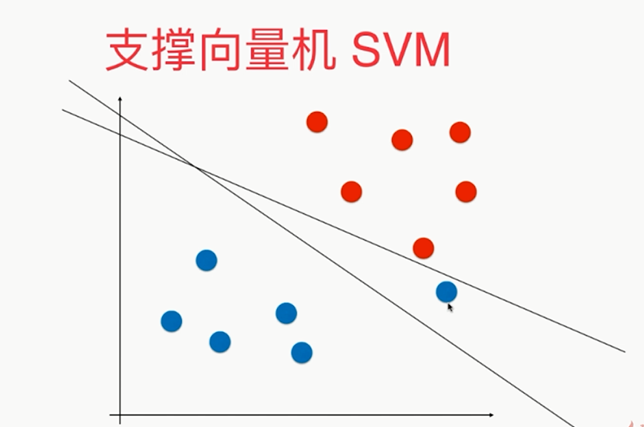 ,
,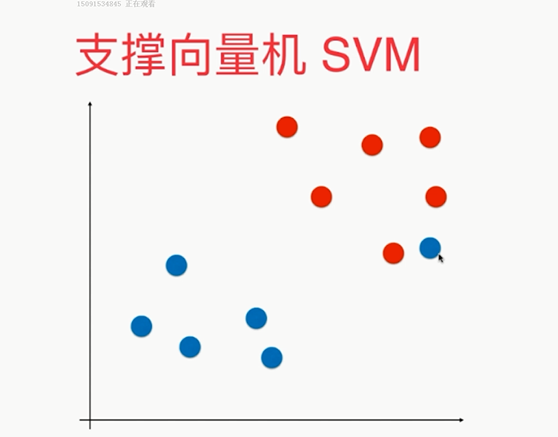
若是这种更不行了,:因此需soft margin SVM
 ,
,
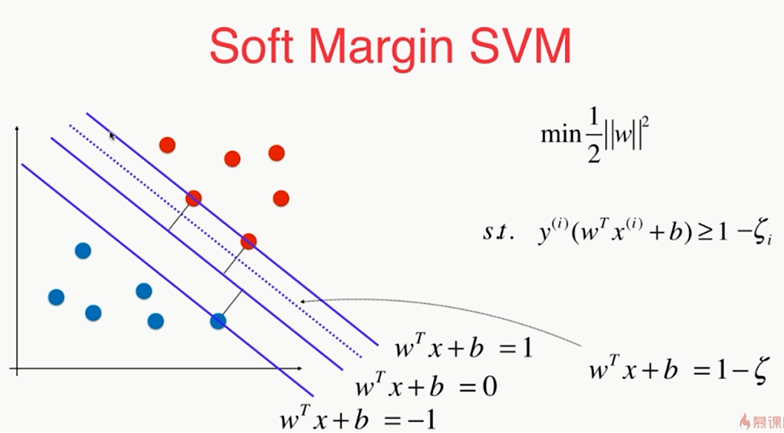 ,
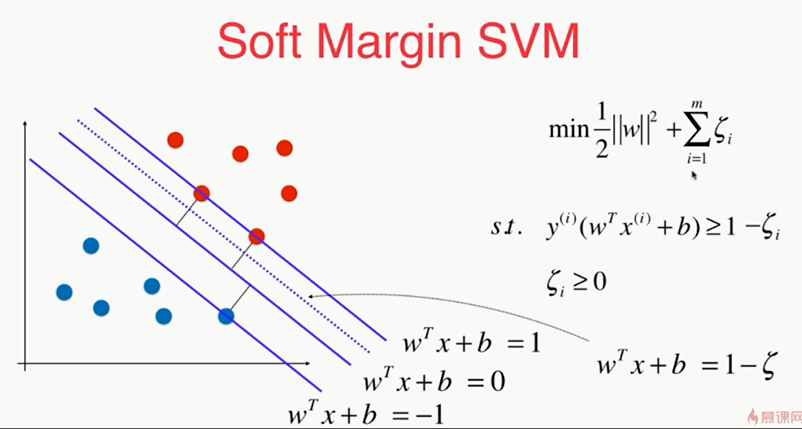
,
 ,
,
此时称L1正则

scikit-learn中的SVM
实际使用SVM:和kNN一样,要做数据标椎化处理!
涉及距离!!!
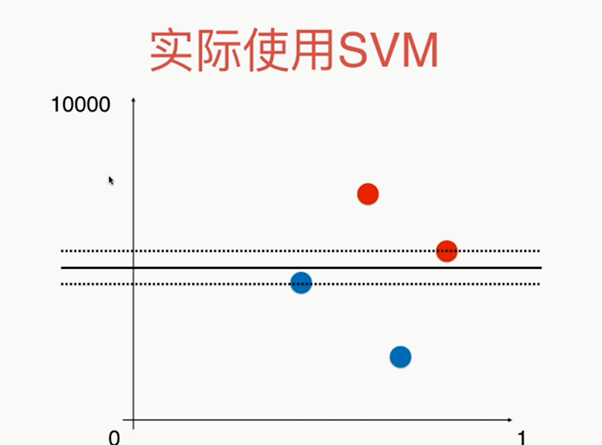 ,
,
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1,1),
np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1,1)
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmp = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])
plt.contourf(x0, x1, zz,cmap=custom_cmp) plot_decision_boundary(svc,axis=[-3,3,-3,3])
plt.scatter(X_standard[y==0,0],X_standard[y==0,1])
plt.scatter(X_standard[y==1,0],X_standard[y==1,1])
plt.show()
plot_decision_boundary
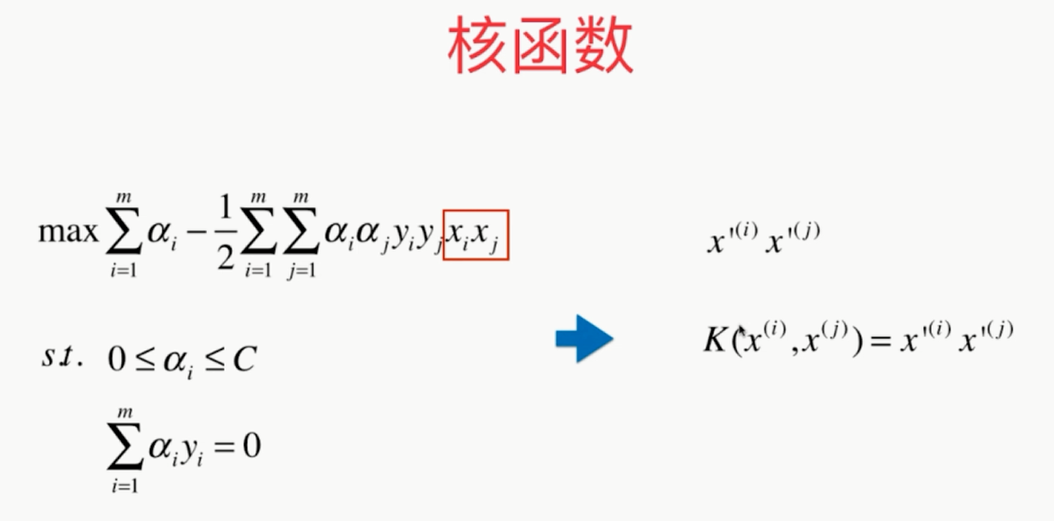
什么是核函数?
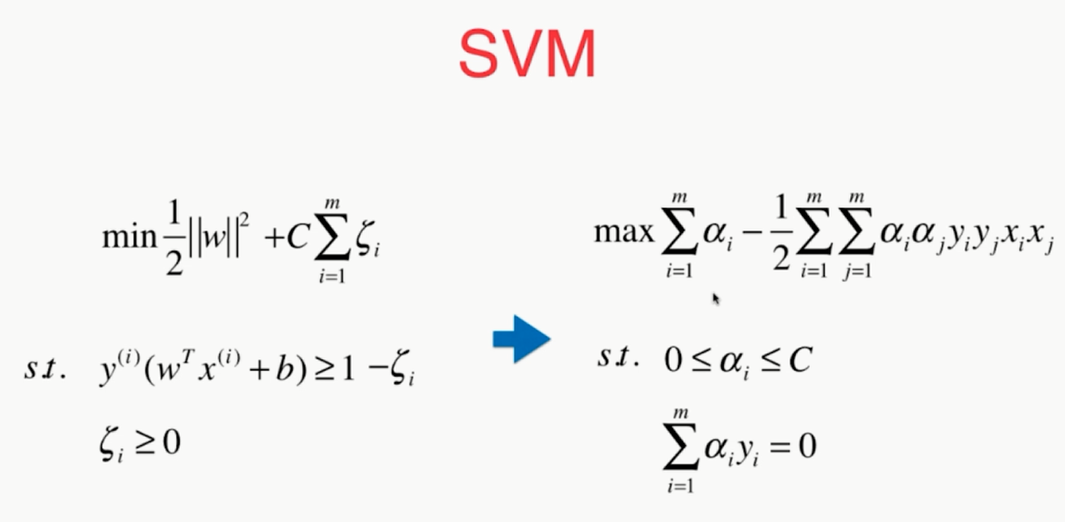 ,
,
 ,
,
 ,
, ,
,
 ,
,

高斯核函数亦称径向基函数:

 ,
,
 ,
,
 ,
,
scikit-learn中的高斯核函数:

SVM思想解决回归问题
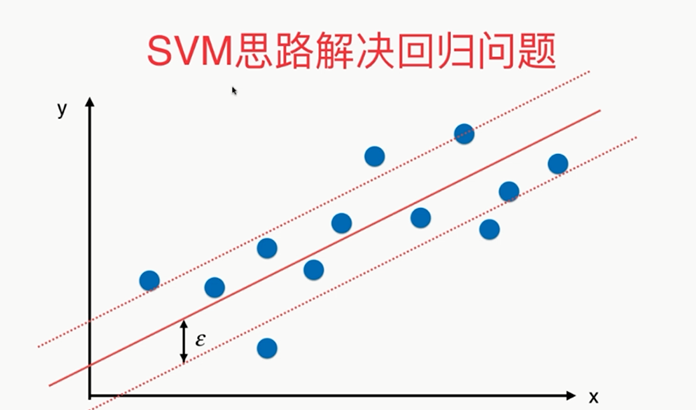
第11章 支撑向量机SVM的更多相关文章
- 走过路过不要错过 包你一文看懂支撑向量机SVM
假设我们要判断一个人是否得癌症,比如下图:红色得癌症,蓝色不得. 看一下上图,要把红色的点和蓝色的点分开,可以画出无数条直线.上图里黄色的分割更好还是绿色的分割更好呢?直觉上一看,就是绿色的线更好.对 ...
- 8.支撑向量机SVM
1.什么是SVM 下面我们就来介绍一些SVM(Support Vector Machine),首先什么是SVM,它是做什么的?SVM,中文名是支撑向量机,既可以解决分类问题,也可以解决回归问题,我们来 ...
- SVM学习笔记-线性支撑向量机
对于PLA算法来说,最终得到哪一条线是不一定的,取决于算法scan数据的过程. 从VC bound的角度来说,上述三条线的复杂度是一样的 Eout(w)≤Ein0+Ω(H)dvc= ...
- 统计学习方法:支撑向量机(SVM)
作者:桂. 时间:2017-05-13 21:52:14 链接:http://www.cnblogs.com/xingshansi/p/6850684.html 前言 主要记录SVM的相关知识,参考 ...
- 支撑向量机(SVM)
转载自http://blog.csdn.net/passball/article/details/7661887,写的很好,虽然那人也是转了别人的做了整理(最原始文章来自http://www.blog ...
- 支撑矢量机SVM
1.线性SVM 首先,回顾一下SVM问题的定义,如下: 线性约束很烦,不方便优化,是否有一种方法可以将线性约束放到优化问题本身,这样就可以无拘无束的优化,而不用考虑线性约束了.其对应的拉格朗日对偶形式 ...
- 模式识别笔记3-支持向量机SVM
1. 线性SVM 对两类点的划分问题,这里对比下逻辑回归和SVM的区别: 逻辑回归的思想是,将所有点到决策平面的距离作为损失来进行训练,目标是到决策平面的距离和最小 SVM的思想是,只关注支持向量(图 ...
- SVM支撑向量机原理
转自:http://blog.csdn.net/v_july_v/article/details/7624837 目录(?)[-] 支持向量机通俗导论理解SVM的三层境界 前言 第一层了解SVM 1分 ...
- 机器学习实战笔记(Python实现)-05-支持向量机(SVM)
--------------------------------------------------------------------------------------- 本系列文章为<机器 ...
随机推荐
- Forrester:开源APM发展势头强劲
在企业的运营团队看来,系统的稳定性和可靠运行时间是至关重要的.因此,企业更乐意向能够负责的技术提供商购买开发完整的.有文档记录的,并且有售后支持的工具或软件. 一般来说,运营团队没有额外精力来应付新奇 ...
- CF思维联系--CodeForces -214C (拓扑排序+思维+贪心)
ACM思维题训练集合 Furik and Rubik love playing computer games. Furik has recently found a new game that gre ...
- C. Cave Painting(最小公倍数的应用)
\(\color{Red}{网上的题解都是投机取巧啊,虽然也没错}\) \(Ⅰ.先说一下投机取巧的方法\) \(自己写几个例子会发现k很小的时候满足条件的n就变得很大\) \(所以我们直接暴力从1判断 ...
- maven基本配置
1.maven 是一个项目构建工具,如果在公司做大的项目 ,需要把项目拆分成很多子项目,为了方便各子项目之间协同开发和调试,一般都会使用maven.使用maven和以前web项目最大的不同是jar包的 ...
- spring mvc实现转发和重定向
转发:服务器端请求的跳转 同一个请求之内 重定向:客户端请求的跳转 两次请求 转发和重定向的区别: 1,转发地址栏不会发生变化,重定向地址栏会发生变化. 2,转发请求的参数不会丢失 重定向参数会丢失. ...
- 【x64软路由】OpenWrt(LEDE) 20200329编译 反追踪 抗污染 加速 PSW 无缝集成 UPnP NAS
固件说明 基于Lede OpenWrt R2020.3.19版本(源码更新截止20200329)Lienol Feed及若干自行维护的软件包 结合家庭x86软路由场景需要定制 按照家庭应用场景对固件及 ...
- Android 源码结构分析
源码版本:AOSP_7.1.1 硬件平台:Rockchip 由于工作要求,需要对rockchip平台的安卓系统进行剪裁.安卓源码比较庞大,会让人感到无从下手,对此,有必要了解一下源码的大致目录结构以及 ...
- YOLOV4所用到的一些tricks
原文链接:http://arxiv.org/abs/2004.10934 整体框架 Bag of Freebies(BoF) & Bag of Specials (BoS) B ...
- Istio的流量管理(实操一)(istio 系列三)
Istio的流量管理(实操一)(istio 系列三) 使用官方的Bookinfo应用进行测试.涵盖官方文档Traffic Management章节中的请求路由,故障注入,流量迁移,TCP流量迁移,请求 ...
- Asp.Net Core 3.1学习-读取、监听json配置文件(7)
1.前言 文件配置提供程序默认的给我们提供了ini.json.Xml等.都是读取不同格式的文件.文件配置提供程序支持文件可寻.必选.文件变更的监视. 2.读取配置文件 主要运用的包:需要Ini.xml ...
