PCA的原理简述

PCA的实质就是要根据样本向量之间的相关性排序，去掉相关性低的信息，也就是冗余的特征信息。

我们都知道噪声信号与待测量的信号之间实际上是没有相关性的，所以我我们利用这个原理就可以将与待测量无关的噪声信号PCA去噪

PCA的原理也就是它的简单的实现过程就是：

首先将样本数据构造成对应的数据矩阵，然后求取该数据矩阵的协方差矩阵，协方差矩阵实际上就是表示随机向量之间的相关性的矩阵，那么为什么协方差矩阵可以表示随机向量之间的相关性呢？

协方差矩阵是怎么求解的呢？我们都知道方差实际上表示的是数据偏离中心的程度，方差越大越偏离中心。那么可以理解协方差表示的是任意两个样本之间的相关程度。

仿照方差的定义：

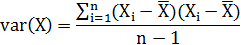
来度量各个维度偏离其均值的程度，协方差可以这样来定义：

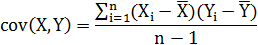
接下来就是求解协方差矩阵的特征值和特征向量，那么关于特征值与特征向量（特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征是什么，可以将每一个特征向量理解为一个线性的子空间，我们可以利用这些线性的子空间干很多的事情。不过，特征值分解也有很多的局限，比如说变换的矩阵必须是方阵。https://jingyan.baidu.com/article/3065b3b68c6bb6becff8a488.html），根据特征值对特征向量进行排序就可以得到特征直方图，抽取其中的几个维度的特征向量组成特征矩阵，这个矩阵就是所谓的投影矩阵，然后用投影矩阵对原样本数据做一个转换（即相乘的过程）。这样就得到了提取特征值下的处理数据结果了。