欧拉工程第68题：Magic 5-gon ring

题目链接

任意一条线上的三个数的和都等于9，顺时针，从最小的外圈开始，得到的序列是：432621213

和             序列

9位的字符串；三角环所能形成的最大字符串为432621513。

使用数字1到10，通过不同的安排，可以得到16位或17位的字符串。五角环所能形成的最大的16位的字符串是什么？

16位的字符，10在外圈

17位的字符，10在内圈

求最大的字符串

6,7,8,9,10应该在外圈，1,2,3,4,5在内圈

2*(1+2+3+4+5) +6+7+8+9+10 = 70，每三个数的和是14

下面其实可以手工做出来了

以外圈最小的数开始：6，在1-5找出两个数使得这三个数的和是14只有5,3，最大数，5要在中间

外圈数还剩：7,8,9,10，内圈数还剩：1,2,4.在3所在的线上还差11，只有10+1=11

外圈数还剩：7,8,9,内圈数还剩：2,4.在1所在的线上还差13，只有9+4=11

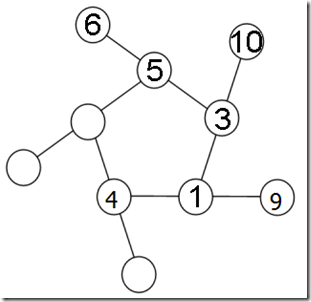
外圈数还剩：7，8，内圈数还剩：2

下面就是这样的了

答案就是：6531031914842725

下面用Python暴露破解

导入产生排列的包

from itertools import permutations

下面你该知道怎么做了吧

遍历所有的排列，选择满足上面条件的数

全部程序 ：

from itertools import permutations

import time as time

def run():
    digits=['1','2','3','4','5','6','7','8','9','10']
    perm =  permutations(digits)
    res = 0
    for p in perm:
        arr = map(int,p)
        candidate =      p[0] + p[1] + p[2] +\
                         p[3] + p[2] + p[4]+\
                         p[5] + p[4] + p[6]+\
                         p[7] + p[6] + p[8]+\
                         p[9] + p[8] + p[1];
    #     print candidate
        if arr[0] > arr[3] or arr[0]> arr[5] or arr[0] > arr[7] or arr[0]> arr[9]:continue
        if arr[1]==10 or arr[2]==10 or arr[4]==10 or arr[8] ==10 :continue
        if (arr[0]+arr[1]+arr[2]) != (arr[3] + arr[2] + arr[4]) :continue
        if (arr[0]+arr[1]+arr[2]) != (arr[5] + arr[4] + arr[6]) :continue
        if (arr[0]+arr[1]+arr[2]) != (arr[7] + arr[6] + arr[8]) :continue
        if (arr[0]+arr[1]+arr[2]) != (arr[9] + arr[8] + arr[1]) :continue
        if int(candidate)>res and len(candidate)==16:
            res = int(candidate)
#             print res ,arr

    print res

if __name__ == '__main__':
    start = time.time()
    run()
    print "running time:",(time.time() - start),'s'

结果

6531031914842725
running time: 30.3180000782 s

这个时间真是太长了。

package project61;

public class P68{
    int[] p = {1,2,3,4,5,6,7,8,9,10};
    void run(){
        for(int i=1;i<20;i++){
            GetNextPerm();
            System.out.println(""+p[0]+p[1]+p[2]+p[3]+p[4]+p[5]+p[6]+p[7]+p[8]+p[9]);
        }

        String result="";
        while(true){
            if(!GetNextPerm()) break;
            if(CheckResult()){
                String candidate ="" + p[0] + p[1] + p[2]
                                + p[3] + p[2] + p[4]
                                + p[5] + p[4] + p[6]
                                + p[7] + p[6] + p[8]
                                + p[9] + p[8] + p[1];
                System.out.println(candidate);
            }
        }

    }
    // 类似于快速排序
    boolean GetNextPerm(){
        int N = p.length;
        int i= N -1;
        while(p[i-1]>=p[i]){
            i--;
            if(i<1) return false;
        }
        int j = N;
        while(p[j-1]<=p[i-1]){
            j = j-1;
        }
        swap(i-1,j-1);
        i++;
        j=N;
        while(i<j){
            swap(i-1,j-1);
            i++;
            j--;
        }

        return true;

    }
    boolean CheckResult(){
        if(p[1]==10||
           p[2]==10||
           p[4]==10||
           p[8]==10) return false;
        if(p[0] > p[3]||
           p[0] > p[5]||
           p[0] > p[7]||
           p[0] > p[9]) return false;
        if(p[0] + p[1]+ p[2] != p[3] + p[2] +p[4]) return false;
        if(p[0] + p[1]+ p[2] != p[5] + p[4] +p[6]) return false;
        if(p[0] + p[1]+ p[2] != p[7] + p[6] +p[8]) return false;
        if(p[0] + p[1]+ p[2] != p[9] + p[8] +p[1]) return false;
        return true;
    }
    void swap(int i,int j){
        int k=p[i];
        p[i] = p[j];
        p[j] = k;
    }
    public static void main(String[] args){
        long t0 = System.currentTimeMillis();
        new P68().run();
        long t1 = System.currentTimeMillis();
        System.out.println("running time:"+(t1 - t0)+"ms");
    }
}

这个自己参数所以的排列，再找满足条件的数

程序跑的倒是很快

6531031914842725
running time:77ms

参考链接