WC前的颓废——带花树

QAQ现在很不想写题解博客那就来写个算法吧QAQ...

带花树

题目

来看个题...

UOJ79.

某机房里有\(n\)个OIer，其中有\(n\)个男生，\(0\)个女生。现在他们要两两配对。

有\(m\)个关系，每个关系是一个无序对\((a_i,b_i)\)，表示这两个人之间愿意配对。

求：最多能配成多少对，并找出一组方案。

说人话：一般图最大匹配。

算法

既然是匹配，我们能不能直接模仿匈牙利算法呢？答案是不可以（废话，可以的话还要什么带花树啊）。

原因是：我们在二分图中，如果dfs找增广路时经过某个点找不到，那么我们可以证明这一轮中这个点的确是无用的（也即，这一轮里所有的增广路都不经过这个点），于是我们就能保证每个点至多走一遍，时间复杂度得到保证。

但是如果是一般图，这个性质不一般成立。比如下图：

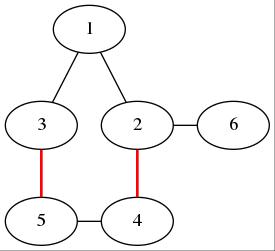
图中红线是已匹配的边。那么，如果我从\(1\)开始dfs时先经过\(2\)，那么接下来就只能到\(4\)（因为只能走匹配边），然后是\(5,3\)，同时我们会给这四个节点都打一个“找不到增广路”的标记。

但是实际上存在\(1\rightarrow3\rightarrow5\rightarrow4\rightarrow2\rightarrow6\)这条增广路。仔细观察我们就能发现：这种现象之所以存在，是由于奇环\(1-3-5-4-2-1\)的存在（如果没有奇环，就变成了二分图匹配，这时候匈牙利算法就是对的）。

那么，对于奇环，有什么后果呢？显然，如果我们dfs出了一个奇环，那么无论环上那个点dfs出了增广路都是可行的。（例如，上图中，如果从\(5\)处dfs出一条增广路，使得\(5\)匹配到别的点且\(3\)成为未盖点，那么可以走\(1-3\)。同样，如果\(5\)被孤立，我们可以走\(1-2-4-5\)来把\(5\)匹配上）

于是，我们可以把一个奇环当做一个点（这个奇环被称为“花”，这就是带花树名字的来历），然后继续找增广路。

形式化的，如果我们在图\(G=(V,E)\)中找到了一个奇环\(v_1-v_2-\dots-v_k-v_1\)（称为“花”），其中\(v_1\)是环上的深度最小的结点，不难证明，\(v_1\)的配偶不在此话中（因为在找到这个花之前所有边组成一个二分图，那么由于\(v_1\)向下dfs/bfs出了一个花，它一定是X结点，只有X结点会向外扩展），且\((v_2,v_3),(v_4,v_5)\dots(v_{k-1},v_{k})\)都是匹配边。那么我们构建一个图

\[\begin{aligned}G'&=(V', E'),\\ V'&=V/\{v_2,v_3\dots,v_k\},\\ E'&=\{(f(a),f(b))|(a,b)\in E, a,b\neq v_i, i=1\dots k\}\end{aligned}
\]

其中\(f(v_i)=v_1, f(a)=a(a\neq v_j), i, j=1,2,\dots,k\)

并且原本\(G\)中的所有匹配除掉\((v_2,v_3),(v_4,v_5)\dots(v_{k-1},v_{k})\)构成\(G'\)的一个匹配。

那么，\(G\)中存在增广路\(\Leftrightarrow\)\(G'\)中存在增广路。

证明：

\(\Rightarrow\)：对于\(G\)中的任意一条增广路，若其不经过这朵花，那么在\(G'\)中也存在这条增广路；否则，令这条从\(s\)开始的增广路上的最后一个在花上的点为\(v_j\)，那么这条增广路形如 \(s\leadsto v_j \leadsto t\)，我们在\(G'\)上构造如下增广路：先从\(s \leadsto v_1 \leadsto t\)，其中第一段路程沿着bfs/dfs树走，第二段路程沿着原图中的增广路走，唯一不同的是\(v_j\)变成了\(v_1\)（这是合法的，因为所有从\(v_j\)出发的边都被连到了\(v_1\)上，而且我们根据所有\(v\)都是已盖点可以知道\(v_j\)出发的边是非匹配边）。

\(\Leftarrow\)：对于\(G'\)中的一条增广路，若它不经过\(v_1\)，则\(G\)中也存在；否则，设这条增广路为\(s\leadsto v_1\rightarrow x \leadsto t\)（\(x\)可能等于\(t\)），根据\(E'\)的定义存在\((v_i, x)\in E\)，从而我们构造\(G\)中的增广路：\(s\leadsto v_1\leadsto v_i \rightarrow x \leadsto t\)，其中第一段和第三段不变（因为增广路上\(v_1\)至多出现1次，所以这两段在\(G\)中存在），第二段是在花里走（或者精确一点，若\(i\)是奇数，走\(v_1\rightarrow v_2 \dots v_i\)，否则走\(v_1\rightarrow v_k \dots v_i\)。证毕。

bfs时，我们可以\(O(n)\)求出LCA并\(O(kn)\)缩花，从而单次bfs至多\(O(n^2)\)，总复杂度至多\(O(n^3)\)。

实现上，我们不实际缩点，而是对于每个点维护一个\(fa\)，表示它所处的最大的花的LCA（就是\(v_1\)）。由于花里可能还有花，这个\(fa\)要用并查集维护。在证明中构造增广路是通过判断\(i\)奇偶性，但实际上我们可以直接维护每个点要往哪边走，也即维护一个\(link_i\)表示如果\(i\)失配要和谁匹配（例如，\(link_{v_2}=v_1,link_{v_3}=v_4\)）。找LCA的时候直接暴力\(O(n)\)，但要注意只找每个并查集的根节点（因为非根节点都缩到花里了）；缩花时要注意如果两个点已经在一朵花里就不要再缩了。

代码

#include <algorithm>
#include <cstdio>
const int N = 550;
const int M = 250050;
int pre[N], nxt[M], to[M], cnt, n;
int vis[N], fa[N], link[N], mate[N];
int que[N], head, tail;
int ss[N], time;
inline void addEdge(int x, int y) {
  nxt[cnt] = pre[x];
  to[pre[x] = cnt++] = y;
}
int Find(int x) { return fa[x] == x ? x : fa[x] = Find(fa[x]); }
int LCA(int x, int y) {
  ++time;
  while (ss[x] != time) {
    if (x) {
      ss[x] = time;
      x = Find(link[mate[x]]);
    }
    std::swap(x, y);
  }
  return x;
}
void flower(int x, int y, int p) {
  while (Find(x) != p) {
    link[x] = y;
    fa[y = mate[x]] = fa[x] = p;
    if (vis[y] == 1)
      vis[que[tail++] = y] = 2;
    x = link[y];
  }
}
bool match(int x) {
  head = tail = 0;
  for (int i = 1; i <= n; ++i)
    vis[fa[i] = i] = 0;
  vis[que[tail++] = x] = 2;
  while (head != tail) {
    x = que[head++];
    for (int i = pre[x]; ~i; i = nxt[i]) {
      int u = to[i];
      if (!vis[u]) {
        vis[u] = 1;
        link[u] = x;
        if (mate[u])
          vis[que[tail++] = mate[u]] = 2;
        else {
          while (u) {
            x = mate[link[u]];
            mate[mate[u] = link[u]] = u;
            u = x;
          }
          return true;
        }
      } else if (vis[u] == 2 && Find(u) != Find(x)) {
        int p = LCA(x, u);
        flower(x, u, p);
        flower(u, x, p);
      }
    }
  }
  return false;
}
int main() {
  int m, x, y, ans = 0;
  scanf("%d%d", &n ,&m);
  std::fill(pre + 1, pre + n + 1, -1);
  while (m--) {
    scanf("%d%d", &x, &y);
    addEdge(x, y);
    addEdge(y, x);
    if (!mate[x] && !mate[y])
      mate[mate[x] = y] = x, ++ans;
  }
  for (int i = 1; i <= n; ++i)
    if (!mate[i] && match(i))
      ++ans;
  printf("%d\n", ans);
  for (int i = 1; i <= n; ++i)
    printf("%d ", mate[i]);
  return 0;
}