P3629 [APIO2010]巡逻

题目描述

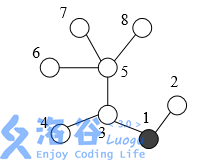
在一个地区中有 n 个村庄，编号为 1, 2, ..., n。有 n – 1 条道路连接着这些村庄，每条道路刚好连接两个村庄，从任何一个村庄，都可以通过这些道路到达其他任一个村庄。每条道路的长度均为 1 个单位。为保证该地区的安全，巡警车每天要到所有的道路上巡逻。警察局设在编号为 1 的村庄里，每天巡警车总是从警察局出发，最终又回到警察局。下图表示一个有 8 个村庄的地区，其中村庄用圆表示（其中村庄 1 用黑色的圆表示），道路是连接这些圆的线段。为了遍历所有的道路，巡警车需要走的距离为 14 个单位，每条道路都需要经过两次。

为了减少总的巡逻距离，该地区准备在这些村庄之间建立 K 条新的道路，每条新道路可以连接任意两个村庄。两条新道路可以在同一个村庄会合或结束（见下面的图例（c））。一条新道路甚至可以是一个环，即，其两端连接到同一个村庄。由于资金有限，K 只能是 1 或 2。同时，为了不浪费资金，每天巡警车必须经过新建的道路正好一次。下图给出了一些建立新道路的例子：

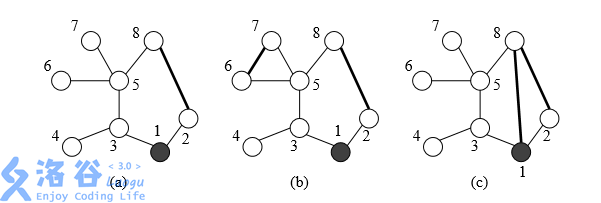
在(a)中，新建了一条道路，总的距离是 11。在(b)中，新建了两条道路，总的巡逻距离是 10。在(c)中，新建了两条道路，但由于巡警车要经过每条新道路正好一次，总的距离变为了 15。试编写一个程序，读取村庄间道路的信息和需要新建的道路数，计算出最佳的新建道路的方案使得总的巡逻距离最小，并输出这个最小的巡逻距离。

输入输出格式

输入格式：

第一行包含两个整数 n, K(1 ≤ K ≤ 2)。接下来 n – 1 行，每行两个整数 a, b，表示村庄 a 与 b 之间有一条道路(1 ≤ a, b ≤ n)。

输出格式：

输出一个整数，表示新建了 K 条道路后能达到的最小巡逻距离。

输入输出样例

输入样例#1：

输出样例#1：

输入样例#2：

输出样例#2：

输入样例#3：

输出样例#3：

说明

10%的数据中，n ≤ 1000, K = 1；

30%的数据中，K = 1；

80%的数据中，每个村庄相邻的村庄数不超过 25；

90%的数据中，每个村庄相邻的村庄数不超过 150； 100%的数据中，3 ≤ n ≤ 100,000, 1 ≤ K ≤ 2。

Solution：

　　本题ZYYS。

　　题意给出了一棵树，由1出发最后回到1，每条边都得走2次，所以一定得走$2(n-1)$的距离，然后可以加1或2条新边（可以连接任意两个点，点可以相同），新边必须至少走1次，求最小化距离。

　　当我们加入一条边，原树就存在一个环，环上的边可以只走1次，设环的长度为$len$，我们就要最大化$len$。

　　而$len-1$就是原树上的一条简单路径，要使$len$最大，那么$len-1$显然是树的直径。

　　对于$k=1$的情况，只要求出直径就能算出答案了。

　　对于$k=2$的情况，先求出一条直径，再对直径路径上的边权取反（类似于最大流中的反向边的作用），这样第二次求直径就不会和上次的冲突，即使两者有重复的部分因为边取反了，所以等价于抵消掉重合部分，答案还是照常算就好了，坑点是第二次求直径有负边，所以不能两边dfs（或bfs），只能dp去求（证明就是第二个样例），其次就是第二次直径可能为负值，直接把其当作0（因为新边可以连本身）。

代码：

/*Code by 520 -- 8.17*/
#include<bits/stdc++.h>
#define il inline
#define ll long long
#define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++)
#define Bor(i,a,b) for(int (i)=(b);(i)>=(a);(i)--)
using namespace std;
const int N=;
int ans,n,m,to[N],net[N],h[N],cnt=,p,c[N],d[N],tot,pre[N],w[N],mx;
bool vis[N];
 
int gi(){
    int a=;char x=getchar();
    while(x<''||x>'')x=getchar();
    while(x>=''&&x<='')a=(a<<)+(a<<)+(x^),x=getchar();
    return a;
}
 
il void add(int u,int v){to[++cnt]=v,net[cnt]=h[u],h[u]=cnt,w[cnt]=;}
 
il void bfs(int s){
    queue<int>q;
    memset(c,-0x3f,sizeof(c));
    memset(vis,,sizeof(vis));
    memset(d,,sizeof(d));
    q.push(s),vis[s]=,c[s]=;
    while(!q.empty()){
        int u=q.front();q.pop();
        for(int i=h[u];i;i=net[i])
            if(!vis[to[i]]) d[to[i]]=u,pre[to[i]]=i,c[to[i]]=c[u]+w[i],q.push(to[i]),vis[to[i]]=;
    }
    mx=-;
    For(i,,n) if(c[i]>mx)p=i,mx=c[i];
}
 
int f[N];
 
void dp(int u){
    vis[u]=;
    for(int i=h[u];i;i=net[i])
        if(!vis[to[i]]){
            dp(to[i]);
            mx=max(mx,f[u]+f[to[i]]+w[i]);
            f[u]=max(f[u],f[to[i]]+w[i]);
        }
}
 
int main(){
    n=gi(),m=gi();
    int u,v;
    For(i,,n-) u=gi(),v=gi(),add(u,v),add(v,u);
    bfs(),bfs(p);
    for(int i=p;i;i=d[i]) w[pre[i]]=w[pre[i]^]=-;
    ans=(n-<<)-mx+;
    if(m==)cout<<ans,exit();
    else {
        mx=-,memset(vis,,sizeof(vis));
        dp();
        mx=mx<?:mx;
        ans=ans-mx+;
        cout<<ans;
    }
    return ;
}