028-B+树(一)

B+ 树

这部分主要学习：什么是B+树？

了解了 B 树后再来了解下它的变形版：B+ 树，它比 B 树的查询性能更高。

一棵 B+ 树需要满足以下条件：

1. 节点的子树数和关键字数相同（B 树是关键字数比子树数少一）
2. 节点的关键字表示的是子树中的最大数，在子树中同样含有这个数据
3. 叶子节点包含了全部数据，同时符合左小右大的顺序

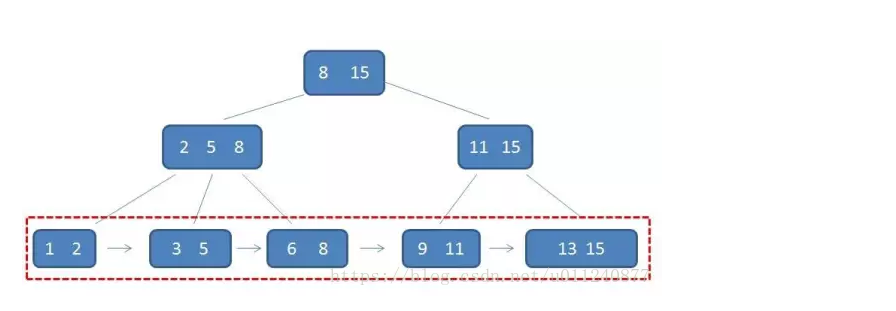
简单概括下 B+ 树的三个特点：

1. 关键字数和子树相同
2. 非叶子节点仅用作索引，它的关键字和子节点有重复元素
3. 叶子节点用指针连在一起

首先第一点不用特别介绍了，在 B 树中，节点的关键字用于在查询时确定查询区间，因此关键字数比子树数少一；而在 B+ 树中，节点的关键字代表子树的最大值，因此关键字数等于子树数。

第二点，除叶子节点外的所有节点的关键字，都在它的下一级子树中同样存在，最后所有数据都存储在叶子节点中。

根节点的最大关键字其实就表示整个 B+ 树的最大元素。父节点的每个数据都是其对应子节点的最大值

第三点，叶子节点包含了全部的数据，并且按顺序排列，B+ 树使用一个链表将它们排列起来，这样在查询时效率更快。

由于 B+ 树的中间节点不含有实际数据，只有子树的最大数据和子树指针，因此磁盘页中可以容纳更多节点元素，也就是说同样数据情况下，B+ 树会 B 树更加“矮胖”，因此查询效率更快。

B+ 树的查找必会查到叶子节点，更加稳定。

有时候需要查询某个范围内的数据，由于 B+ 树的叶子节点是一个有序链表，只需在叶子节点上遍历即可，不用像 B 树那样挨个中序遍历比较大小。

B+ 树的三个优点：

1. 层级更低，IO 次数更少
2. 每次都需要查询到叶子节点，查询性能稳定
3. 叶子节点形成有序链表，范围查询方便