NOIP模拟

1.要选一个{1,2,...n}的子集使得假如a和b在所选集合里且(a+b)/2∈{1,2,...n}那么(a+b)/2也在所选集合里

f[i]=2*f[i-1]-f[i-2]+g[i]

g[n]:选1，n的方案数

观察性质，模拟+元素的过程推知集合中元素是等差数列，且公差=1(mod 2)

故g[n] = n-1的奇约数

f长这样:

1 : 2
2 : 4
3 : 7
4 : 12
5 : 18
6 : 26
7 : 36
8 : 48
9 : 61
10 : 77
11 : 95
12 : 115
13 : 137
14 : 161
15 : 187
16 : 217
17 : 248
18 : 281
19 : 317

2.（7）.Ever Forever

将一个数的置换看做一条有向边，最后得到的图是很多环（入度=出度=0）。

求每个环初始与最终是否循环同构，并求相差距离，构出一个x=a[i](mod b[i])的方程组

判定方程组x=a[i] (mod b[i])是否有整数根

（1）暴力解，可能会爆long long

（2）将b[i]分解质因数，对于每个p,求出a[i] % (p^k)，若有矛盾则不成立

a%b=c可规约到a%p1=c%p1; a%p2=c%p2; 若p次数>1，则同理

3.字符消除——尽可能长的t使得S的长度为t的前后缀循环同构。

M1：枚举总长度——如果在1~i和n-i+1~n这一段字母acsii和相同则在做下一步判断

考虑循环同构性质

在S中枚举A，即S长为|A|的前后缀相同，考虑在删去前后各|A|个字符的S中如何快速求出最长的B。
定义f[i]为|A|=i时B的最大长度。 ==> f[i]-2≤f[i+1]

4.

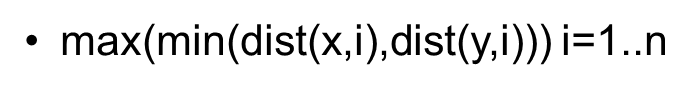
方法1

借助直径搞一搞，求两点连到直径上的点（a,b），预处理每个直径上点到分支的最长距离，RMQ处理(序号+dis)的最大值，

---

至于中间那一部分，观察到点到询问点间距离均单调，得到一个Border就可以RMQ询问啦

lalala一遍过rank1

方法2 ：暴力求中间点，维护最长链次长链+倍增

找到mid，分两半考虑。

大概是这样。 次长链是为了防止最长链的终点为询问中的x点的子孙（即经过mid后回到x）

max(f1(x),f2(x)) 值在f1(x)或f2(x)中任意一个取到Max时得到

5.bitset优化高斯消元

每一个位置取还是不取设一个变量，然后分每一个质因子考虑就可以列出一些异或方程，解有几个自由元就好了。——jiry_2

对于每个质因数，将所有该因数的次数为奇数的变量异或起来=0

对于每行每列，所有数异或起来=1

答案=2的k次幂

（取奇数个，取偶数个这种东西，是异或方程组的经典题目）

6. （这题是大结论性质难题，等以后变强了继续啃这些推导过程）

本原串：一个字符串s除|s|以外的周期，都不是|s|的约数，则称s是本原串。（不会存在形如aaaa的串，a=string）

若p, q ∈ Per(s)且 p + q <= |s|，则gcd(p, q) ∈ Per(s)

如果一个串不是本原串，修改其中任意一个字符，它就会变成本原串。(eg. ababab --> ababaa)

定义PS(s)为s的所有前后缀的长度组成的集合。即PS(s) = {x | s[1, x]是s的前后缀}

规定0 不属于 PS(s), 而|s| ∈ PS(s)

=>PS(s) = {next[|s|], next[next[|s|]], next[next[next[|s|]]], ...}

将PS(s)里的元素从小到大排序，得到p[1], p[2], p[3], ..., p[|PS(s)|]。(eg. p={1,3,4,7})

//p就是把PS中的元素列出来

再设 strP[i] 为 PS(r) = {p[1], p[2], ... p[i]}的字典序最小的01串。当然了……|strP[i]| = p[i]

(strP[|PS(s)|] = 最终答案, p[|PS(s)|] = len(s))

从strP[1]..strP[|PS(s)|]顺序递推

1.p[i+1]<=p[i]*2，则strP[i]一定是strP[i + 1]的前后缀。 只需将strP[i]后加上长为p[i+1]-p[i]的后缀，得到strP[i+1]

2.中间全接0或末尾扔一个1

结论：若有一个字符串P，设U = P . "0" * j . P，则不存在q，|P| < q < |U|，使得q ∈ PS(U)的充要条件是P . "0" * j是本原串。

KMP：每次在后面添加一个字符，在后面删除一个字符，维护next数组，均摊O(1)

字符串s不是本原串当且仅当它的最小周期不为|s|且最小周期是|s|的约数。

{

1.KMP得到PS集合，得到p[]

2.初始strP[0] ：

if p[1] = 1 then strP[1] = "0"

else strP[1] = ("0" * (p[1] - 1)) . "1";

3.递推得到每一个p[]对应的strP[], strP[|PS(s)|]即为答案

}

7.三角形面积S=

->     ->

x   *  y  / 2 = |x1y2-x2y1| / 2

可通过行列式、割补法等求（计算几何）

通过极角坐标排序可去掉绝对值，求叉积之和可通过前缀和解决。

8. [No.9]第三题(disanti)  容斥原理

思想很简单：容斥，判一判某种方案是否符合“匹配”的定义，（就算某种情况值=0，容斥也是正确的）就好了。 //大家的做法好像都用dfs，然后几乎没有什么预处理？ 我写的好复杂。。

我的思路是枚举每个集合，判可行性，再求类似边权和的东西。事先维护 1.一个集合所有点都不选的最大匹配权值和　　2.A中每个点分别到B中所有点的边权和

(如果没有集合间的关系，可以O(k^2)求上1，即简单的容斥 ==> 应用广泛)

O(2^k*k) //如果不加一些优化可能退化成O(2^k*n)或O(2^k*k^2)

但是，犯了很多小错，比如数组大小。。　　（类似状压的题，数组大小要小心啊）

总之，这大概是容斥的大致模板了吧。

9. [No.9]第一题(diyiti) 压位

每次询问把整块的部分扔到一起，多出部分特判即可，细节超多

{

这种题全是位运算, '&' --> "&&"就狗带了

2串长度不同

修改时在原string中也要修改

}

反正考场上一般来说都不太敢打这种东西

压位的正确姿势好像是32位一起，unsigned int