网格弹簧质点系统模拟（Spring-Mass System by Verlet Integration）附源码

　　模拟物体变形最简单的方法就是采用弹簧质点系统（Spring-Mass System），由于模型简单并且实用，它已被广泛应用于服饰、毛发以及弹性固体的动态模拟。对于三角网格而言，弹簧质点系统将网格中的顶点看作系统中的质点，而网格的边则是连接这些质点的弹簧。这样，弹簧质点系统模型就将物体简化成由弹簧和质点组成的系统，并利用弹簧质点的运动规律来描述物体的弹性变形过程。

　　Verlet积分是求解牛顿运动方程的数值方法，原理简单描述如下：首先将系统t+dt时刻的位置x(t+dt)以及系统t-dt时刻的位置x(t-dt)用泰勒公式展开：

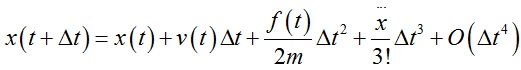
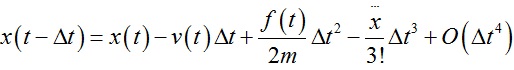
　　上面两式相加后得到：

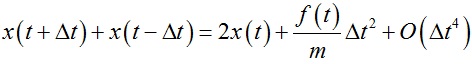
　　进一步变化得到：

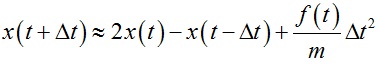
　　因此通过上式可以根据系统前两时刻的状态求解系统的当前状态，这与”基于网格的波动方程模拟“一文中的求解过程有些类似。

　　为了真实模拟物体变形效果，需要对弹簧质点系统进行受力分析：1. 每个质点有自身重力的影响；2. 每个质点受到与它相连的弹簧弹力影响，弹簧弹力遵守胡克定律；3. 质点运动时受到与其速度成正比的阻尼约束；4. 质点会受到其他外力的影响，由于施加的外力在每个三角面片上有一个法向分量，我们只需对每个质点周围三角片上的这些分量相加即可。

% constrains option
wind = false;
ball = true;
pins = false;

figure('Position', [, , , ]);
fh = drawMesh(V,F,'facecolor','y','edgecolor','none');
if ball
    center = [  -];
    radius = ;
    drawSphere([center radius], 'facecolor','r', 'nPhi',, 'nTheta',);
end
if pins
    plot3([-;], [;], [;], 'k-', 'linewidth',);
end
view([- ])
axis equal
axis off
axis([-  -  - ]);
camlight
lighting gouraud

set(gca, 'position', [   ]);

% initial condition
x_pre = V;
x_cur = V;

% rest length
E = edges(F);
l0 = vectorNorm3d(V(E(:,),:) - V(E(:,),:)); 

nV = size(V,);
draw_t = ;
tic;
while true
    % spring force
    Fs = stiffness * (vectorNorm3d(x_cur(E(:,),:) - x_cur(E(:,),:)) - l0);
    dir = normalizeVector3d(x_cur(E(:,),:) - x_cur(E(:,),:));

    M1 = sparse(E, E, [Fs.*dir(:,);-Fs.*dir(:,)]);
    M2 = sparse(E, E, [Fs.*dir(:,);-Fs.*dir(:,)]);
    M3 = sparse(E, E, [Fs.*dir(:,);-Fs.*dir(:,)]);
    as = [diag(M1), diag(M2), diag(M3)] ./ m;

    % wind force
    aw = zeros(nV,);
    if wind
        N = normalizeVector3d(normals(x_cur,F));
        Fw = N * wind_force(i/)' .* wind_strength;

        M1 = sparse(F, F, repmat(Fw.*N(:,),,));
        M2 = sparse(F, F, repmat(Fw.*N(:,),,));
        M3 = sparse(F, F, repmat(Fw.*N(:,),,));
        aw = [diag(M1), diag(M2), diag(M3)] ./ m;
    end

    % verlet integration with a simple damping model
    x_new = drag*(x_cur - x_pre) + x_cur + bsxfun(@plus, as+aw, g)*dt*dt;

    x_pre = x_cur;
    x_cur = x_new;

    % ball constrains
    if ball
        diff = bsxfun(@minus, x_cur, center);
        index = vectorNorm3d(diff) < radius+;
        x_cur(index,:) = bsxfun(@plus, center, bsxfun(@times, normalizeVector3d(diff(index,:)), radius+));
    end

    % pin constrains
    if pins
        x_pre(pin_idx,:) = V(pin_idx,:);
        x_cur(pin_idx,:) = V(pin_idx,:);
    end

    % updata figure
    if toc > 0.033
        set(fh, 'Vertices', x_cur);
        drawnow;
        tic;
    end
end

本文为原创，转载请注明出处：http://www.cnblogs.com/shushen。