将递归函数非递归化的一般方法(cont)

本文通过模拟汇编里的stack机制，构建一个自己的stack，然后将上一篇blog末尾的递归函数void bst_walk(bst_node_t *root)非递归化。

o libstack.h

 #ifndef _LIBSTACK_H
 #define _LIBSTACK_H

 #ifdef    __cplusplus
 extern "C" {
 #endif

 typedef void * uintptr_t; /* generic pointer to any struct */

 uintptr_t *stack_init(size_t size);
 void stack_fini();
 int stack_isFull();
 int stack_isEmpty();
 void push(uintptr_t e);
 void pop(uintptr_t *e);

 #ifdef    __cplusplus
 }
 #endif

 #endif /* _LIBSTACK_H */

o libstack.c

 #include <stdio.h>
 #include <stdlib.h>
 #include "libstack.h"

 /**
  * Basic Stack OPs are supported, including:
  *
  * 1. Construct/Destruct a stack
  * 2. Tell stack is full or empty
  * 3. push() and pop()
  *
  * == DESIGN NOTES ==
  *
  * There are 3 static variables reserved,
  *
  *     ss: stack segment
  *     sp: stack pointer
  *     sz: stack size
  *
  * And the stack looks like:
  *
  *               | RED | ss[-1]  ; SHOULD NEVER BE ACCESSED
  *     low-addr  +-----+ <------------TopOfStack-----------
  *        ^      |     | ss[0]
  *        |      |     | ss[1]
  *        |      | ... |
  *        |      |     |
  *        |      |     | ss[sz-1]
  *        |      +-----+ <------------BottomOfStack--------
  *     high-addr | RED | ss[sz]  ; SHOULD NEVER BE ACCESSED
  *
  * (1) If (sp - ss) == 0,  stack is full
  * (2) If (sp - ss) == sz, stack is empty
  * (3) Push(E): { sp -= 1;   *sp = E; }
  * (4) Pop(&E): { *E  = *sp; sp += 1; }
  */

 static uintptr_t *ss = NULL; /* stack segment */
 static uintptr_t *sp = NULL; /* stack pointer */
 static size_t sz = ;        /* stack size */

 int stack_isFull()  { return (sp == ss); }
 int stack_isEmpty() { return (sp == ss + sz); }

 uintptr_t *
 stack_init(size_t size)
 {
     ss = (uintptr_t *)malloc(sizeof (uintptr_t) * size);
     if (ss == NULL) {
         fprintf(stderr, "failed to malloc\n");
         return NULL;
     }

     sz = size;
     sp = ss + size;
     return ss;
 }

 void
 stack_fini()
 {
     free(ss);
 }

 void
 push(uintptr_t e)
 {
     sp -= ;
     *sp = e;
 }

 void
 pop(uintptr_t *e)
 {
     *e = *sp;
     sp += ;
 }

1. 一旦栈被初始化后，栈指针sp一定是指向栈底，*sp不可访问（尤其是写操作），因为不在分配的内存有效范围内；

2. 对于入栈操作(push), 第一步是将sp-=1, 第二步是写入要入栈的元素 (*sp = E); (因为初始化后*sp的内存不可写，所以push操作一定率先改写sp)

3. 对于出栈操作(pop), 顺序与push相反，第一步取出sp指向的内存地址里的内容(E = *sp), 第二步才是将sp+=1;

o foo.c (简单测试)

 /**
  * A simple test against stack OPs, including:
  * o stack_init(),   stack_fini()
  * o stack_isFull(), stack_isEmpty()
  * o push(), pop()
  */

 #include <stdio.h>
 #include "libstack.h"

 static void
 dump_stack(uintptr_t *ss, size_t size)
 {
     (void) printf("%p: ", ss);
     for (int i = ; i < size; i++) {
         if (ss[i] != NULL)
             (void) printf("%-10p ", *(ss+i));
         else
             (void) printf("0x%-8x ", 0x0);
     }
     printf("\n");
 }

 int
 main(int argc, char *argv[])
 {
     size_t size = ;

     uintptr_t *ss = stack_init(size);
     dump_stack(ss, size);

     for (int i = ; !stack_isFull(); i++) {
         push((uintptr_t)(ss+i));
         dump_stack(ss, size);
     }

     (void) printf("\n");

     uintptr_t e = NULL;
     for (; !stack_isEmpty();) {
         pop(&e);
         (void) printf(" (pop) got %-10p\n", e);
     }

     stack_fini();

     return ;
 }

o Makefile

 CC      = gcc
 CFLAGS  = -g -Wall -std=gnu99 -m32
 INCS    =

 TARGET  = foo

 all: ${TARGET}

 foo: foo.o libstack.o
     ${CC} ${CFLAGS} -o $@ $^

 foo.o: foo.c
     ${CC} ${CFLAGS} -c $< ${INCS}

 libstack.o: libstack.c libstack.h
     ${CC} ${CFLAGS} -c $<

 clean:
     rm -f *.o
 clobber: clean
     rm -f ${TARGET}

o 编译和运行测试

$ make
gcc -g -Wall -std=gnu99 -m32 -c foo.c
gcc -g -Wall -std=gnu99 -m32 -c libstack.c
gcc -g -Wall -std=gnu99 -m32 -o foo foo.o libstack.o

$ ./foo
0x8ecc008: 0x0        0x0        0x0        0x0
0x8ecc008: 0x0        0x0        0x0        0x8ecc008
0x8ecc008: 0x0        0x0        0x8ecc00c  0x8ecc008
0x8ecc008: 0x0        0x8ecc010  0x8ecc00c  0x8ecc008
0x8ecc008: 0x8ecc014  0x8ecc010  0x8ecc00c  0x8ecc008

 (pop) got 0x8ecc014
 (pop) got 0x8ecc010
 (pop) got 0x8ecc00c
 (pop) got 0x8ecc008
$

测试简单且直接，不解释。如果还不确信，可以用gdb调试。

现在对上一篇blog末尾的递归函数使用上面实现的stack进行去递归化改写，改写后的代码如下：

 void
 bst_walk(bst_node_t *root)
 {
     if (root == NULL)
         return;

     (void) stack_init(STACK_SIZE);

     while (root != NULL || !stack_isEmpty()) {
         if (root != NULL) {
             push((uintptr_t)root);
             root = root->left;
             continue;
         }

         pop((uintptr_t *)(&root));
         printf("%d\n", root->key);

         root = root->right;
     }

     stack_fini();
 }

为方便阅读，下面给出使用meld进行diff后的截图，

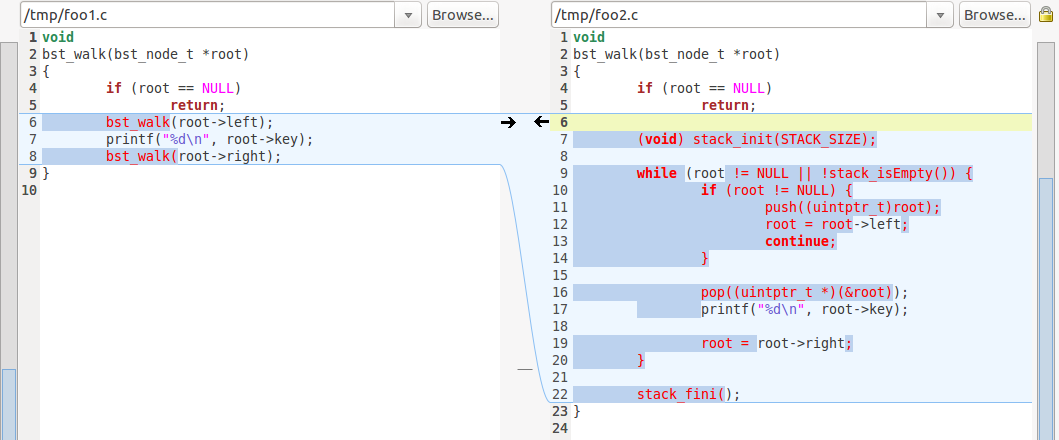
• L7: 构建一个stack, 其中STACK_SIZE是一个宏
• L22: 将stack销毁
• L9-14: 首先遍历左子树，不断将结点压入栈中，直到到达最左的叶子结点，那么则执行L16-17 （最左的叶子结点也会被压入栈中）
• L16-17: 出栈并打印结点的key
• L19: 将新的根结点设置为刚刚出栈的结点的右儿子， 重新执行L9-17， 直到所有结点都被遍历到(当然, stack为空)

注： 左图中的函数使用了两次递归，所以将其转化成非递归函数的难度相对较大。