CoderForces999E-Reachability from the Capital

E. Reachability from the Capital

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

There are nn cities and mm roads in Berland. Each road connects a pair of cities. The roads in Berland are one-way.

What is the minimum number of new roads that need to be built to make all the cities reachable from the capital?

New roads will also be one-way.

Input

The first line of input consists of three integers nn, mm and ss (1≤n≤5000,0≤m≤5000,1≤s≤n1≤n≤5000,0≤m≤5000,1≤s≤n) — the number of cities, the number of roads and the index of the capital. Cities are indexed from 11 to nn.

The following mm lines contain roads: road ii is given as a pair of cities uiui, vivi (1≤ui,vi≤n1≤ui,vi≤n, ui≠viui≠vi). For each pair of cities (u,v)(u,v), there can be at most one road from uu to vv. Roads in opposite directions between a pair of cities are allowed (i.e. from uu to vv and from vv to uu).

Output

Print one integer — the minimum number of extra roads needed to make all the cities reachable from city ss. If all the cities are already reachable from ss, print 0.

Examples

input

Copy

9 9 1
1 2
1 3
2 3
1 5
5 6
6 1
1 8
9 8
7 1

output

Copy

3

input

Copy

5 4 5
1 2
2 3
3 4
4 1

output

Copy

1

Note

The first example is illustrated by the following:

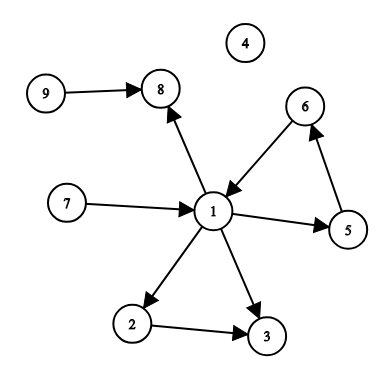
For example, you can add roads (6,46,4), (7,97,9), (1,71,7) to make all the cities reachable from s=1s=1.

The second example is illustrated by the following:

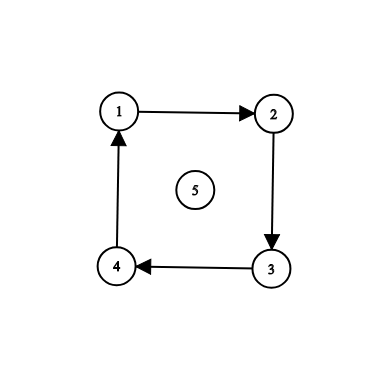
In this example, you can add any one of the roads (5,15,1), (5,25,2), (5,35,3), (5,45,4) to make all the cities reachable from s=5s=5.

题意：就是给你很多条路，这些路，城市之间的是无向的，而城市与首都之间的只能由首都到达城市不能由城市到首都。

题解：用到了拓扑图，我们可以把不能通到首都的城市加一条需边使其能到达城市，然后遍历每一条虚边，如果新加的虚边能够使前面加的虚边联通的城市联通，则取消原来的标记。最后标记的数量即为答案；

AC代码为：

#include<bits/stdc++.h>
using namespace std;
const int maxn=5010;
int n,m,k,u,v,tot,cnt;
int first[maxn],vis[maxn],judge[maxn],connect[maxn];

struct Node{
    int to,net;
} node[maxn<<1];

void Init()
{
    tot=1,cnt=0;
    memset(first,-1,sizeof first);
}

void add(int u,int v)
{
    node[tot].to=v;
    node[tot].net=first[u];
    first[u]=tot++; 
}

void dfs(int st)
{
    vis[st]=connect[st]=1;
    for(int e=first[st];e!=-1;e=node[e].net)
    {
        int v=node[e].to;
        if(!vis[v])
        {
            judge[v]=0;
            dfs(v);
        }
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin>>n>>m>>k;
    Init();
    for(int i=0;i<m;i++) 
    {
        cin>>u>>v;
        add(u,v);
    }
    dfs(k);
    memset(vis,0,sizeof vis);
    for(int i=1;i<=n;i++)
    {
        if(!connect[i])
        {
            judge[i]=1;
            dfs(i);
            memset(vis,0,sizeof vis);
        }
    }
    for(int i=1;i<=n;i++) if(judge[i]) cnt++;
    cout<<cnt<<endl;
    return 0;
}