[数学基础]奇异值分解SVD

　　之前看到过很多次奇异值分解这个概念，但我确实没有学过。大学线性代数课教的就是坨屎，我也没怎么去上课，后来查了点资料算是搞清楚了，现在写点东西总结一下。

　　奇异值分解，就是把一个矩阵拆成一组矩阵之和。在数学里面，因式分解，泰勒展开，傅里叶展开，特征值分解，奇异值分解都是这个路数。就是把当前数据表示成一组某种意义下互相独立的数据叠加的形式。目的在于简化计算处理或舍弃次要信息。

　　　　　　　　　　数学表达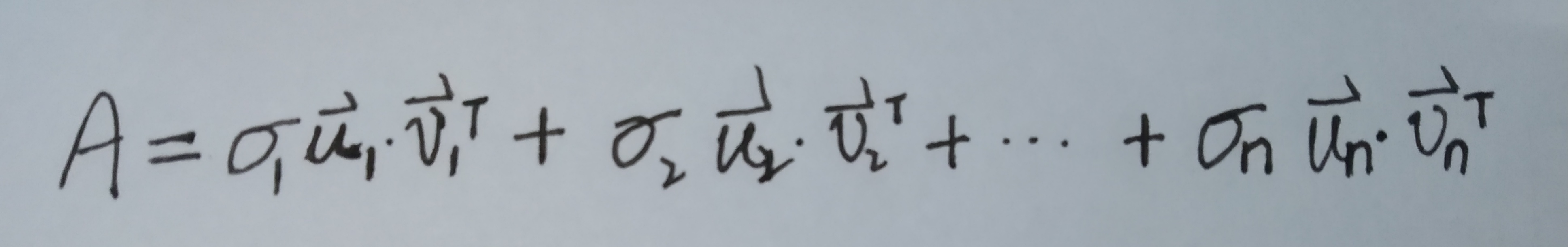：或

　　其中系数是每一项的奇异值，u，v是列向量，可以发现每一项的都是秩为一的矩阵，我们人为假定。跟矩阵特征值分解在形式上还是有很大相似之处的。

　　每个矩阵都可以表示成多个秩为一的矩阵的和，而每一项前的系数也就是奇异值的大小反映了这一项相对于A的权重大小。

　　然后说一下SVD的物理应用，主要举例图像压缩与图像去噪。

　　图像压缩，即适当降低图像精度，假设矩阵A表示了目标图片，对A作SVD分解，那么我们把A的分解式末端权重较小的部分舍弃(或者说只保留前面权重大的若干项)，那么这张图片所需存储量便大大降低了，进而达到了图像压缩。

　　图像去噪，如果一副图像包含噪声，我们有理由相信那些较小的奇异值就是由噪声引起的。例如图像矩阵A奇异值分解后得到的奇异值为：15.29，7.33，5.23，4.16，0.24，0.03。最后两项相对于前面几项权重太小了，把它们舍掉，便直观地看出图像噪声减少了。