python 树与二叉树的实现
1.树的基本概念
1.树的定义
树的定义是递归的，树是一种递归的数据结构。
1）树的根结点没有前驱结点，除根结点之外所有结点有且只有一个前驱结点
2）树中所有结点可以有零个或多个后继结点
2.树的术语
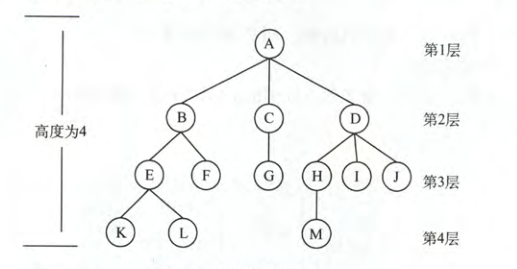
1）B是K的祖先结点，K是B的子孙结点，E是K的双亲结点，K是E的孩子结点，K是L的兄弟结点
2）树中一个结点的子节点个数为该结点的度，树中结点最大度数为树的度
3）度大于0为节点结点，度等于0为叶子结点
4）结点层次如图，结点深度是从根结点从顶往下累加，结点高度从低往上累加，树的高度（深度）是树的最大层数
5）有序树：从左到右有次序，有关联。反之为无序树
6）两结点之间的路径是两个结点之间所经过的结点序列构成的，路径长度是路径上所经过的边的个数
7）森林是m(m>=0)棵互不相交的树的集合
2.二叉树的概念
1.二叉树的定义
至多只有两颗子树，二叉树有左右之分，次序不能颠倒，也是递归形式定义
1）或者为空二叉树，即n=0
2）或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树
二叉树与度为2的有序树的区别：
1）度为2的树至少有3个结点，而二叉树可以为空
2）左右次数
2.几个特殊的二叉树
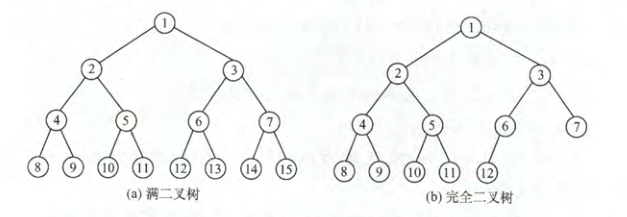
1）满二叉树
2）完全二叉树
3）二叉排序树
一棵二叉树或者是空二叉树，如：左子树上所有关键字均小于根结点的关键字，右子树上的所有结点的关键字均大于根结点的关键字，左子树和右子树又各是一棵二叉排序树
4）平衡二叉树
树上任何一结点的左子树和右子树的深度之差不超过1
3.二叉树的python3实现
import operator class BinaryTree:
"""
A recursive implementation of Binary Tree
Using links and Nodes approach. Modified to allow for trees to be constructed from other trees
rather than always creating a new tree in the insert_feft or insert_right
""" def __init__(self, key):
"""Create new tree"""
self._key = key
self._child_left = None
self._child_right = None def get_root_val(self):
"""Get root key value"""
return self._key def set_root_val(self, key):
"""Set root key value"""
self._key = key root = property(get_root_val, set_root_val) def get_child_left(self):
"""Get left child"""
return self._child_left def set_child_left(self, node):
"""Set left child"""
self._child_left = node child_left = property(get_child_left, set_child_left) def get_child_right(self):
"""Get right child"""
return self._child_right def set_child_right(self, node):
"""Set right child"""
self._child_right = node child_right = property(get_child_right, set_child_right) def is_leaf(self):
"""Check if a node is leaf"""
return (not self._child_left) and (not self._child_right) def insert_left(self, new_node):
"""Insert left subtree"""
if isinstance(new_node, BinaryTree):
new_subtree = new_node
else:
new_subtree = BinaryTree(new_node) if self._child_left:
new_subtree.set_child_left(self._child_left) self._child_left = new_subtree def insert_right(self, new_node):
"""Insert right subtree"""
if isinstance(new_node, BinaryTree):
new_subtree = new_node
else:
new_subtree = BinaryTree(new_node) if self._child_right:
new_subtree.set_child_right(self._child_right)
self._child_right = new_subtree def preorder(self):
"""Pre-order tree traversal"""
print(self._key, end=" ")
if self._child_left:
self._child_left.preorder()
if self._child_right:
self._child_right.preorder() def inorder(self):
"""In-order tree traversal"""
if self._child_left:
self._child_left.inorder()
print(self._key, end=" ")
if self._child_right:
self._child_right.inorder() def postorder(self):
"""Post-order tree traversal"""
if self._child_left:
self._child_left.postorder()
if self._child_right:
self._child_right.postorder()
print(self._key, end=" ") def print_exp(self):
"""Print an expression"""
if self._child_left:
print("(", end=" ")
self._child_left.print_exp()
print(self._key, end=" ")
if self._child_right:
self._child_right.print_exp()
print(")", end=" ") def postorder_eval(self):
"""Postorder evaluation"""
operations = {
"+": operator.add,
"-": operator.sub,
"*": operator.mul,
"/": operator.truediv,
}
result_1 = None
result_2 = None
if self._child_left:
result_1 = self._child_left.postorder_eval()
if self._child_right:
result_2 = self._child_right.postorder_eval()
if result_1 and result_2:
return operations[self._key](result_1, result_2)
return self._key def height(self):
"""Height of a tree"""
if not self._key:
return -1
if self._child_left:
height_left = self._child_left.height()
else:
height_left = -1 if self._child_right:
height_right = self._child_right.height()
else:
height_right = -1 return 1 + max(height_left, height_right) def __len__(self):
"""Size of a tree"""
return self.size() def size(self):
"""Count nodes in a tree"""
if not self._key:
return 0
if self._child_left:
children_left = self._child_left.size()
else:
children_left = 0 if self._child_right:
children_right = self._child_right.size()
else:
children_right = 0 return 1 + children_left + children_right
4.二叉排序树的python3实现
class BinaryTreeNode:
"""Binary Tree Node class""" def __init__(self, key, value, left=None, right=None, parent=None):
"""Create new Tree Node"""
self._key = key
self._value = value
self._child_left = left
self._child_right = right
self._parent = parent def get_child_left(self):
"""Return the node's left child"""
return self._child_left def set_child_left(self, node):
"""Assign the node's left child"""
self._child_left = node child_left = property(get_child_left, set_child_left) def get_child_right(self):
"""Return the node's right child"""
return self._child_right def set_child_right(self, node):
"""Assign the node's right child"""
self._child_right = node child_right = property(get_child_right, set_child_right) def get_parent(self):
"""Return the node's parent"""
return self._parent def set_parent(self, node):
"""Assign the node's parent"""
self._parent = node parent = property(get_parent, set_parent) def is_child_left(self):
"""Check if the node is a left child"""
return self._parent and self._parent.child_left == self def is_child_right(self):
"""Check if the node is a right child"""
return self._parent and self._parent.child_right == self def is_root(self):
"""Check if the node is a tree root"""
return not self._parent def is_leaf(self):
"""Check if the node is a leaf"""
return not (self._child_right or self._child_left) def has_a_child(self):
"""Check if the node has any child"""
return self._child_right or self._child_left def has_children(self):
"""Check if the node has both children"""
return self._child_right and self._child_left def get_key(self):
"""Get node key"""
return self._key def set_key(self, key):
"""Set node key"""
self._key = key key = property(get_key, set_key) def get_value(self):
"""Get node value"""
return self._value def set_value(self, value):
"""Set node value"""
self._value = value value = property(get_value, set_value) def replace_payload(self, key, value, left, right):
"""Change node payload"""
self._key = key
self._value = value
self._child_left = left
self._child_right = right
if self.child_left:
self._child_left.parent = self
if self.child_right:
self._child_right.parent = self def find_successor(self):
"""Find the node's successor"""
successor = None
if self._child_right:
successor = self._child_right.find_min()
else:
if self._parent:
if self.is_child_left():
successor = self._parent
else:
self._parent.child_right = None
successor = self._parent.find_successor()
self._parent.child_right = self
return successor def find_min(self):
"""Find the smallest node in the right subtree"""
current = self
while current.child_left:
current = current.child_left
return current def splice_out(self):
"""Splice out"""
if self.is_leaf():
if self.is_child_left():
self._parent.child_left = None
else:
self._parent.child_right = None
elif self.has_a_child():
if self.child_left:
if self.is_child_left():
self._parent.child_left = self._child_left
else:
self._parent.child_right = self._child_left
self._child_left.parent = self._parent
else:
if self.is_child_left():
self._parent.child_left = self._child_right
else:
self._parent.child_right = self._child_right
self._child_right.parent = self._parent def __iter__(self):
"""The standard inorder traversal of a binary tree"""
if self:
if self._child_left:
for elem in self._child_left:
yield elem
yield self._key
if self._child_right:
for elem in self._child_right:
yield elem class BinarySearchTree:
"""Binary search tree implementation""" def __init__(self):
self._root = None
self._size = 0 def __len__(self):
"""Tree size"""
return self._size def size(self):
"""Tree size"""
return self._size def __iter__(self):
"""Iterator"""
return self._root.__iter__() def __getitem__(self, key):
"""[] getter operator override"""
result = self.get(key)
if result:
return result
raise KeyError("Error, key not in tree") def get_root(self):
"""Get tree root"""
return self._root def set_root(self, node):
"""Set tree root"""
self._root = node root = property(get_root, set_root) def get(self, key):
"""Retrieve a value by the key"""
if self._root:
result = self._get(key, self._root)
if result:
return result.value
return None
else:
return None def _get(self, key, current_node):
"""Retrieve a value by the key (helper function)"""
if not current_node:
return None
if current_node.key == key:
return current_node
elif key < current_node.key:
return self._get(key, current_node.child_left)
else:
return self._get(key, current_node.child_right) def __setitem__(self, key, value):
"""[] setter operator override"""
self.put(key, value) def put(self, key, value):
"""Add new node"""
if self._root:
self._put(key, value, self._root)
else:
self._root = BinaryTreeNode(key, value)
self._size = self._size + 1 def _put(self, key, value, current_node):
"""Add new node (helper function)"""
if key < current_node.key:
if current_node.child_left:
self._put(key, value, current_node.child_left)
else:
current_node.child_left = BinaryTreeNode(
key, value, parent=current_node
)
else:
if current_node.child_right:
self._put(key, value, current_node.child_right)
else:
current_node.child_right = BinaryTreeNode(
key, value, parent=current_node
) def __contains__(self, key):
"""in operator override"""
return bool(self._get(key, self._root)) def __delitem__(self, key):
"""del operator override"""
self.delete(key) def delete(self, key):
"""Remove a node by its key"""
if self._size > 1:
node_to_remove = self._get(key, self._root)
if node_to_remove:
self._delete(node_to_remove)
self._size = self._size - 1
else:
raise KeyError("Error, key not in tree")
elif self._size == 1 and self._root.key == key:
self._root = None
self._size = self._size - 1
else:
raise KeyError("Error, key not in tree") def _delete(self, current_node):
"""Remove a node by its key (helper function)"""
if current_node.is_leaf(): # removing a leaf
if current_node == current_node.parent.child_left:
current_node.parent.child_left = None
else:
current_node.parent.child_right = None
elif current_node.has_children(): # removing a node with two children
successor = current_node.find_successor()
successor.splice_out()
current_node.key = successor.key
current_node.value = successor.value
else: # removing a node with one child
if current_node.get_child_left():
if current_node.is_child_left():
current_node.child_left.parent = current_node.parent
current_node.parent.child_left = current_node.child_left
elif current_node.is_child_right():
current_node.child_left.parent = current_node.parent
current_node.parent.child_right = current_node.child_left
else:
current_node.replace_payload(
current_node.child_left.key,
current_node.child_left.value,
current_node.child_left.child_left,
current_node.child_left.child_right,
)
else:
if current_node.is_child_left():
current_node.child_right.parent = current_node.parent
current_node.parent.child_left = current_node.child_right
elif current_node.is_child_right():
current_node.child_right.parent = current_node.parent
current_node.parent.child_right = current_node.child_right
else:
current_node.replace_payload(
current_node.child_right.key,
current_node.child_right.value,
current_node.child_right.child_left,
current_node.child_right.child_right,
) def inorder(self):
"""In-order tree traversal"""
self._inorder(self._root) def _inorder(self, tree):
"""In-order tree traversal (helper function)"""
if tree:
self._inorder(tree.child_left)
print(tree.key, end=" ")
self._inorder(tree.child_right) def postorder(self):
"""Post-order tree traversal"""
self._postorder(self._root) def _postorder(self, tree):
"""Post-order tree traversal (helper function)"""
if tree:
self._postorder(tree.child_left)
self._postorder(tree.child_right)
print(tree.key, end=" ") def preorder(self):
"""Pre-order tree traversal"""
self._preorder(self._root) def _preorder(self, tree):
"""Pre-order tree traversal (helper function)"""
if tree:
print(tree.key, end=" ")
self._preorder(tree.child_left)
self._preorder(tree.child_right) def clear(self):
"""Remove all nodes"""
while self._root:
self.delete(self._root.key)
5.平衡二叉树的python3实现
from pythonds3.trees.binary_search_tree import BinarySearchTree
from pythonds3.trees.binary_search_tree import BinaryTreeNode class AVLTreeNode(BinaryTreeNode):
"""AVL Tree Node""" def __init__(self, key, val, balance_factor, left=None, right=None, parent=None):
"""Create an AVL tree node"""
BinaryTreeNode.__init__(self, key, val, left, right, parent)
self._balance_factor = balance_factor def get_balance_factor(self):
"""Get the node balance factor"""
return self._balance_factor def set_balance_factor(self, value):
"""Set the node balance factor"""
self._balance_factor = value balance_factor = property(get_balance_factor, set_balance_factor) class AVLTree(BinarySearchTree):
"""AVL tree implementation""" def __init__(self):
"""Create a new AVL tree"""
BinarySearchTree.__init__(self) def put(self, key, value):
"""Add new node"""
if self._root:
self._put(key, value, self._root)
else:
self._root = AVLTreeNode(key, value, 0)
self._size = self._size + 1 def _put(self, key, value, current_node):
"""Add a new node to the tree (helper function)"""
if key < current_node.key:
if current_node.get_child_left():
self._put(key, value, current_node.child_left)
else:
current_node.child_left = AVLTreeNode(
key, value, 0, parent=current_node
)
self.update_balance(current_node.child_left)
else:
if current_node.get_child_right():
self._put(key, value, current_node.child_right)
else:
current_node.child_right = AVLTreeNode(
key, value, 0, parent=current_node
)
self.update_balance(current_node.child_right) def update_balance(self, node):
"""Update the tree balance"""
if node.balance_factor > 1 or node.balance_factor < -1:
self.rebalance(node)
return
if node.parent:
if node.is_child_left():
node.parent.balance_factor += 1
elif node.is_child_right():
node.parent.balance_factor -= 1 if node.parent.balance_factor != 0:
self.update_balance(node.parent) def rebalance(self, node):
"""Rebalance the tree"""
if node.balance_factor < 0:
if node.child_right.balance_factor > 0:
# Do an LR Rotation
self.rotate_right(node.child_right)
self.rotate_left(node)
else:
# single left
self.rotate_left(node)
elif node.balance_factor > 0:
if node.child_left.balance_factor < 0:
# Do an RL Rotation
self.rotate_left(node.child_left)
self.rotate_right(node)
else:
# single right
self.rotate_right(node) def rotate_left(self, rotation_root):
"""Left rotation"""
new_root = rotation_root.child_right
rotation_root.child_right = new_root.child_left
if new_root.child_left:
new_root.child_left.parent = rotation_root
new_root.parent = rotation_root.parent
if rotation_root.is_root():
self._root = new_root
else:
if rotation_root.is_child_left():
rotation_root.parent.child_left = new_root
else:
rotation_root.parent.child_right = new_root
new_root.child_left = rotation_root
rotation_root.parent = new_root
rotation_root.balance_factor = (
rotation_root.balance_factor + 1 - min(new_root.balance_factor, 0)
)
new_root.balance_factor = (
new_root.balance_factor + 1 + max(rotation_root.balance_factor, 0)
) def rotate_right(self, rotation_root):
"""Right rotation"""
new_root = rotation_root.child_left
rotation_root.child_left = new_root.child_right
if new_root.child_right:
new_root.child_right.parent = rotation_root
new_root.parent = rotation_root.parent
if rotation_root.is_root():
self._root = new_root
else:
if rotation_root.is_child_right():
rotation_root.parent.child_right = new_root
else:
rotation_root.parent.child_left = new_root
new_root.child_right = rotation_root
rotation_root.parent = new_root
rotation_root.balance_factor = (
rotation_root.balance_factor - 1 - max(new_root.balance_factor, 0)
)
new_root.balance_factor = (
new_root.balance_factor - 1 + min(rotation_root.balance_factor, 0)
)
6.最小二叉堆（一种完全二叉树，父结点键值比子结点小）
class BinaryHeap:
"""Minimal Binary Heap""" def __init__(self):
"""Create a heap"""
self._heap = [] def _perc_up(self, cur_idx):
"""Move a node up"""
while (cur_idx - 1) // 2 >= 0:
parent_idx = (cur_idx - 1) // 2
if self._heap[cur_idx] < self._heap[parent_idx]:
self._heap[cur_idx], self._heap[parent_idx] = (
self._heap[parent_idx],
self._heap[cur_idx],
)
cur_idx = parent_idx def _perc_down(self, cur_idx):
"""Move a node down"""
while 2 * cur_idx + 1 < len(self._heap):
min_child_idx = self._get_min_child(cur_idx)
if self._heap[cur_idx] > self._heap[min_child_idx]:
self._heap[cur_idx], self._heap[min_child_idx] = (
self._heap[min_child_idx],
self._heap[cur_idx],
)
else:
return
cur_idx = min_child_idx def _get_min_child(self, parent_idx):
"""Get a smaller child"""
if 2 * parent_idx + 2 > len(self._heap) - 1:
return 2 * parent_idx + 1
if self._heap[2 * parent_idx + 1] < self._heap[2 * parent_idx + 2]:
return 2 * parent_idx + 1
return 2 * parent_idx + 2 def heapify(self, not_a_heap, show_details=False):
"""Build a heap from any list"""
self._heap = not_a_heap[:]
cur_idx = len(self._heap) // 2 - 1
while cur_idx >= 0:
self._perc_down(cur_idx)
cur_idx = cur_idx - 1
if show_details:
print(self._heap) def insert(self, item):
"""Add a new item"""
self._heap.append(item)
self._perc_up(len(self._heap) - 1) def delete(self):
"""Remove an item"""
self._heap[0], self._heap[-1] = self._heap[-1], self._heap[0]
result = self._heap.pop()
self._perc_down(0)
return result def is_empty(self):
"""Check if the heap is empty"""
return not bool(self._heap) def __len__(self):
"""Get heap size"""
return len(self._heap) def __str__(self):
"""Heap as a string"""
return str(self._heap) def __contains__(self, item):
"""__contains__in method override"""
return item in self._heap
python 树与二叉树的实现的更多相关文章
- python数据结构之树和二叉树(先序遍历、中序遍历和后序遍历)
python数据结构之树和二叉树(先序遍历.中序遍历和后序遍历) 树 树是\(n\)(\(n\ge 0\))个结点的有限集.在任意一棵非空树中,有且只有一个根结点. 二叉树是有限个元素的集合,该集合或 ...
- python数据结构树和二叉树简介
一.树的定义 树形结构是一类重要的非线性结构.树形结构是结点之间有分支,并具有层次关系的结构.它非常类似于自然界中的树.树的递归定义:树(Tree)是n(n≥0)个结点的有限集T,T为空时称为空树,否 ...
- python实战--数据结构二叉树
此文将讲述如何用python实战解决二叉树实验 前面已经讲述了python语言的基本用法,现在让我们实战一下具体明确python的用法 点击我进入python速成笔记 先看一下最终效果图: 首先我们要 ...
- python数据结构之二叉树的统计与转换实例
python数据结构之二叉树的统计与转换实例 这篇文章主要介绍了python数据结构之二叉树的统计与转换实例,例如统计二叉树的叶子.分支节点,以及二叉树的左右两树互换等,需要的朋友可以参考下 一.获取 ...
- Python实现打印二叉树某一层的所有节点
不多说,直接贴程序,如下所示 # -*- coding: utf-8 -*- # 定义二叉树节点类 class TreeNode(object): def __init__(self,data=0,l ...
- Java数据结构之树和二叉树（2）
从这里始将要继续进行Java数据结构的相关讲解,Are you ready?Let's go~~ Java中的数据结构模型可以分为一下几部分: 1.线性结构 2.树形结构 3.图形或者网状结构 接下来 ...
- Java数据结构之树和二叉树
从这里开始将要进行Java数据结构的相关讲解,Are you ready?Let's go~~ Java中的数据结构模型可以分为一下几部分: 1.线性结构 2.树形结构 3.图形或者网状结构 接下来的 ...
- lintcode :前序遍历和中序遍历树构造二叉树
解题 前序遍历和中序遍历树构造二叉树 根据前序遍历和中序遍历树构造二叉树. 样例 给出中序遍历:[1,2,3]和前序遍历:[2,1,3]. 返回如下的树: 2 / \ 1 3 注意 你可以假设树中不存 ...
- lintcode: 中序遍历和后序遍历树构造二叉树
题目 中序遍历和后序遍历树构造二叉树 根据中序遍历和后序遍历树构造二叉树 样例 给出树的中序遍历: [1,2,3] 和后序遍历: [1,3,2] 返回如下的树: 2 / \ 1 3 注意 你可 ...
随机推荐
- 企业账号发布APP
做了一个公司内部人使用的项目,公司申请了企业开发者账号.现将企业开发者账号发布app的过成总结如下: 1.生成Certificate Signing Request (CSR)文件 2.2 请求Cer ...
- ABP进阶教程3 - 优化编辑
点这里进入ABP进阶教程目录 我们尝试在新增/编辑界面增加一个下拉框用来代替输入框编辑Status 添加实体 打开领域层(即JD.CRS.Core)的Entitys目录 //用以存放实体对象添加一个类 ...
- [b0030] python 归纳 (十五)_多进程使用Pool
1 usePool.py #coding: utf-8 """ 学习进程池使用 multiprocessing.Pool 总结: 1. Pool 池用于处理 多进程,并不 ...
- 联邦学习 Federated Learning 相关资料整理
本文链接:https://blog.csdn.net/Sinsa110/article/details/90697728代码微众银行+杨强教授团队的联邦学习FATE框架代码:https://githu ...
- 5. git-lab 项目操作
项目操作 一.给成员授权项目权限 之前我们是给组增加成员. 当有的项目需要给组下面的成员授权不一样的时候. 我们需要在项目里面给成员授权权限 点击管理区域 点这个项目 看下图,我们可以看到 现在这 ...
- 简述ECMAScript6新增特性
1.变量 var 可以重复声明.只有函数级的作用域.存在变量提升 let 不能重复声明.有块级作用域.没有变量提升.变量 const 不能重复声明.具有块级作用域.常量 2.箭头函数 a.为了方便而存 ...
- LeetCode 回文串问题
5. Longest Palindromic Substring 647. Palindromic Substrings 解法一:从中心一点向两边扩展,需要考虑中心为一点,中心为两点. 解法二:马拉车 ...
- jieba、NLTK学习笔记
中文分词 - jiebaimport re import jieba news_CN = ''' 央视315晚会曝光湖北省知名的神丹牌.莲田牌“土鸡蛋”实为普通鸡蛋冒充,同时在商标上玩猫腻, 分别注册 ...
- BZOJ1688 「USACO05OPEN」Disease Manangement 背包+状压DP
问题描述 BZOJ1688 题解 背包,在转移过程中使用状压. \(\mathrm{Code}\) #include<bits/stdc++.h> using namespace std; ...
- C++面向对象程序设计学习笔记（6）
多态性 编译时的多态性与运行时的多态性 在面向对象方法中,所谓多态性就是不同对象收到相同信息时,产生不同的行为.在c++程序设计中,即"一个接口,多种方法" 在C++中,多态性的实 ...