（数据科学学习手札70）面向数据科学的Python多进程简介及应用

本文对应脚本已上传至我的Github仓库https://github.com/CNFeffery/DataScienceStudyNotes

一、简介

　　进程是计算机系统中资源分配的最小单位，也是操作系统可以控制的最小单位，在数据科学中很多涉及大量计算、CPU密集型的任务都可以通过多进程并行运算的方式大幅度提升运算效率从而节省时间开销，而在Python中实现多进程有多种方式，本文就将针对其中较为易用的几种方式进行介绍。

二、利用multiprocessing实现多进程

　　multiprocessing是Python自带的用于管理进程的模块，通过合理地利用multiprocessing，我们可以充分榨干所使用机器的CPU运算性能，在multiprocessing中实现多进程也有几种方式。

2.1 Process

　　Process是multiprocessing中最基础的类，用于创建进程，先来看看下面的示例：

single_process.py

import multiprocessing
import datetime
import numpy as np
import os

def job():

    print(f'进程{os.getpid()}开始计算：', datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S'))
    for j in range(100):
        _ = np.sum(np.random.rand(10000000))
    print(f'进程{os.getpid()}结束运算：', datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S'))

if __name__ == '__main__':

    process = multiprocessing.Process(target=job)
    process.start()

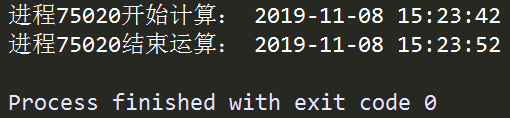
图1 single_process.py运行结果

　　在上面的例子中，我们首先定义了函数job()，其连续执行一项运算任务100次，并在开始和结束的时刻打印该进程对应的pid，用来唯一识别一个独立的进程，接着利用Process()将一个进程实例化，其主要参数如下：

target: 需要执行的运算函数

args: target函数对应的传入参数，元组形式传入

　　在process创建完成之后，我们对其调用.start()方法执行运算，这样我们就实现了单个进程的创建与使用，在此基础上，我们将上述例子多线程化：

multi_processes.py

import multiprocessing
import datetime
import numpy as np
import os

def job():

    print(f'进程{os.getpid()}开始计算：', datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S'))
    for j in range(100):
        _ = np.sum(np.random.rand(10000000))
    print(f'进程{os.getpid()}结束运算：', datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S'))

if __name__ == '__main__':

    process_list = []

    for i in range(multiprocessing.cpu_count() - 1):
        process = multiprocessing.Process(target=job)
        process_list.append(process)

    for process in process_list:
        process.start()

    for process in process_list:
        process.join()

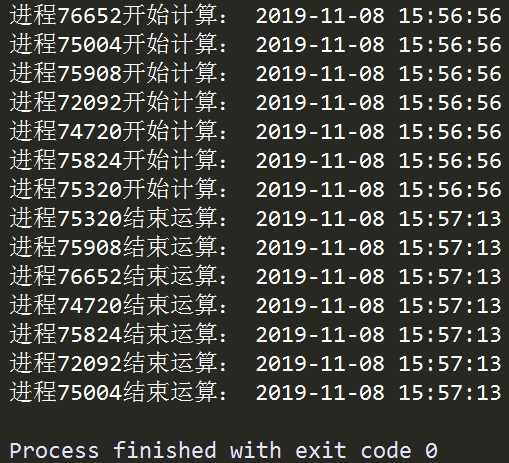
图2 multi_processes.py运行结果

　　在上面的例子中，我们首先初始化用于存放多个线程的列表process_list，接着用循环的方式创建了CPU核心数-1个进程并添加到process_list中，再接着用循环的方式将所有进程逐个激活，最后使用到.join()方法，这个方法用于控制进程之间的并行，如下例：

join_demo.py

import multiprocessing
import os
import datetime
import time

def job():

    print(f'进程{os.getpid()}开始：', datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S'))
    time.sleep(5)
    print(f'进程{os.getpid()}结束：', datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S'))

if __name__ == '__main__':

    process1 = multiprocessing.Process(target=job)
    process2 = multiprocessing.Process(target=job)

    process1.start()
    process1.join()

    process2.start()
    process2.join()
    print('='*200)
    process3 = multiprocessing.Process(target=job)
    process4 = multiprocessing.Process(target=job)

    process3.start()
    process4.start()

    process3.join()
    process4.join()

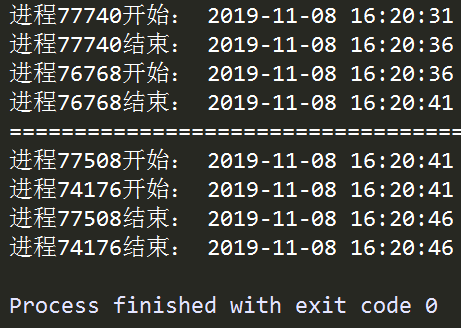
图2 multi_processes.py运行结果

　　观察对应进程执行的开始结束时间信息可以发现，一个进程对象在.start()之后，若在其他的进程对象.start()之前调用.join()方法，则必须等到先前的进程对象运行结束才会接着执行.join()之后的非.join()的内容，即前面的进程阻塞了后续的进程，这种情况下并不能实现并行的多进程，要想实现真正的并行，需要现行对多个进程执行.start()，接着再对这些进程对象执行.join()，才能使得各个进程之间相互独立，了解了这些我们就可以利用Process来实现多进程运算；

2.2 Pool

　　除了上述的Process，在multiprocessing中还可以使用Pool来快捷地实现多进程，先来看下面的例子：

Pool_demo.py

from multiprocessing import Pool
import numpy as np
from pprint import pprint

def job(n):
    return np.mean(np.random.rand(n)), np.std(np.random.rand(n))

if __name__ == '__main__':
    with Pool(5) as p:
        pprint(p.map(job, [i**10 for i in range(1, 6)]))

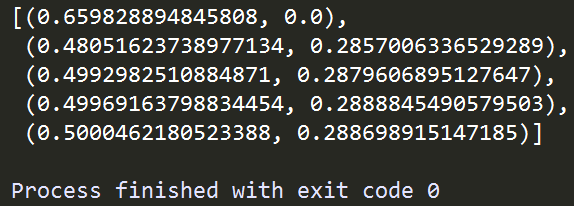
图3 Pool_demo.py运行结果

　　在上面的例子中，我们使用Pool这个类，将自编函数job利用.map()方法作用到后面传入序列每一个位置上，与Python自带的map()函数相似，不同的是map()函数将传入的函数以串行的方式作用到传入的序列每一个元素之上，而Pool()中的.map()方法则根据前面传入的并行数量5，以多进程并行的方式执行，大大提升了运算效率。

三、利用joblib实现多进程

　　与multiprocessing需要将执行运算的语句放置于含有if name == 'main'：的脚本文件中下不同，joblib将多进程的实现方式大大简化，使得我们可以在IPython交互式环境下中灵活地使用它，先看下面这个例子：

from joblib import Parallel, delayed
import numpy as np
import time
import datetime

def job(i):
    start = datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S')
    time.sleep(5)
    end = datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S')

    return start, end

result = Parallel(n_jobs=5, verbose=1)(delayed(job)(j) for j in range(5))
result

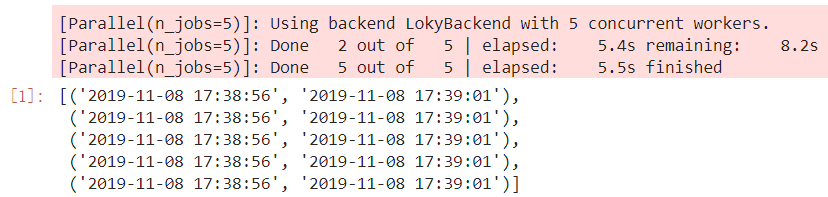
图4 joblib并行示例

　　在上面的例子中，我们从joblib中导入Parallel和delayed，仅用Parallel(n_jobs=5, verbose=1)(delayed(job)(j) for j in range(5))一句就实现了并行运算的功能，其中n_jobs控制并行进程的数量，verbose参数控制是否打印进程运算过程，如果你熟悉scikit-learn，相信这两个参数你一定不会陌生，因为scikit-learn中RandomForestClassifier等可以并行运算的算法都是通过joblib来实现的。

　　以上就是本文的全部内容，如有笔误望指出！