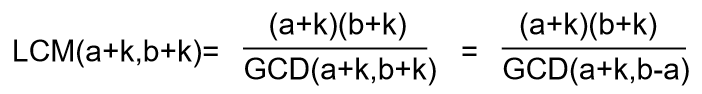Codeforces Round #554 (Div. 2) C. Neko does Maths (数论 GCD(a,b) = GCD(a,b-a))
•题意
给出两个正整数 a,b;
求解 k ,使得 LCM(a+k,b+k) 最小,如果有多个 k 使得 LCM() 最小,输出最小的k;
•思路
时隔很久,又重新做这个题
温故果然可以知新❤
重要知识点
GCD(a,b)=GCD(a,b-a)=GCD(b,b-a) (b>a)
证明:
设GCD(a,b)=c
则a%c=0,b%c=0,(b-a)%c=0
所以GCD(a,b-a)=c
得GCD(a,b)=GCD(a,b-a)
gcd(a+k,b-a)肯定是(b-a)的因子
所以gcd(a+k,b+k)是(b-a)的因子,所以我们就枚举(b-a)的因子(把因子称为i)
使得 (a+k)为i的倍数
解出k,再判断lcm是否符合最小
注意这里枚举的i只是(a+k)和(b+k)的公约数,不一定是最大公约数gcd
两者的公约数得到的是公倍数 公倍数=a*b/公约数
如果是最大公约数的话两者的公倍数一定是最小,
这里是没有甄别是否是最大公约数而是简单的得到公约数,然后得到的是公倍数
在所有的公倍数中,最小公倍数是最小的
所以并不影响解最小公倍数的答案
例如:
12 30
12 30
公约数i=1 k=1 a+k=13 b+k=31 公倍数=403
公约数i=2 k=2 a+k=14 b+k=32 公倍数=224
公约数i=3 k=3 a+k=15 b+k=33 公倍数=165
公约数i=6 k=6 a+k=18 b+k=36 公倍数=108
公约数i=9 k=6 a+k=18 b+k=36 公倍数=72
公约数i=18 k=6 a+k=18 b+k=36 公倍数=36最小公约数36,此时k=6
另外一个思路可以求最大公约数 然后求最小公倍数,看HHHyacinth的博客
•代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll a,b;
ll ans,lcm=0x3f3f3f3f3f3f3f3f;
int main()
{
cin>>a>>b;
ll d=abs(a-b);
for(ll i=;i*i<=d;i++)
{
if(d%i==)//枚举b-a的因数i
{
ll k=(i-a%i)%i;//把a凑成i的倍数需要+k
ll t=(a+k)*(b+k)/i;// a*b/i得公倍数
if(t<lcm)
{
lcm=t;
ans=k;
} ll ii=d/i;
k=(ii-a%ii)%ii;
t=(a+k)*(b+k)/ii;
if(t<lcm)
{
lcm=t;
ans=k;
}
}
}
cout<<ans<<endl;
}
Codeforces Round #554 (Div. 2) C. Neko does Maths (数论 GCD(a,b) = GCD(a,b-a))的更多相关文章
- Codeforces Round #554 (Div. 2) C.Neko does Maths (gcd的运用)
题目链接:https://codeforces.com/contest/1152/problem/C 题目大意:给定两个正整数a,b,其中(1<=a,b<=1e9),求一个正整数k(0&l ...
- Codeforces Round #554 (Div. 2) C. Neko does Maths (简单推导)
题目:http://codeforces.com/contest/1152/problem/C 题意:给你a,b, 你可以找任意一个k 算出a+k,b+k的最小公倍数,让最小公倍数尽量小,求出 ...
- Codeforces Round #554 (Div. 2) C. Neko does Maths(数学+GCD)
传送门 题意: 给出两个整数a,b: 求解使得LCM(a+k,b+k)最小的k,如果有多个k使得LCM()最小,输出最小的k: 思路: 刚开始推了好半天公式,一顿xjb乱操作: 后来,看了一下题解,看 ...
- Codeforces Round #554 (Div. 2) 1152B. Neko Performs Cat Furrier Transform
学了这么久,来打一次CF看看自己学的怎么样吧 too young too simple 1152B. Neko Performs Cat Furrier Transform 题目链接:"ht ...
- Codeforces Round #554 (Div. 2) 1152A - Neko Finds Grapes
学了这么久,来打一次CF看看自己学的怎么样吧 too young too simple 1152A - Neko Finds Grapes 题目链接:"https://codeforces. ...
- Codeforces Round #554 (Div. 2) B. Neko Performs Cat Furrier Transform(思维题+log2求解二进制位数的小技巧)
传送门 题意: 给出一个数x,有两个操作: ①:x ^= 2k-1; ②:x++; 每次操作都是从①开始,紧接着是② ①②操作循环进行,问经过多少步操作后,x可以变为2p-1的格式? 最多操作40次, ...
- Codeforces Round #554 (Div. 2) E Neko and Flashback (欧拉路径 邻接表实现(当前弧优化..))
就是一欧拉路径 贴出邻接表欧拉路径 CODE #include <bits/stdc++.h> using namespace std; const int MAXN = 100005; ...
- Codeforces Round #554 (Div. 2) F2. Neko Rules the Catniverse (Large Version) (矩阵快速幂 状压DP)
题意 有nnn个点,每个点只能走到编号在[1,min(n+m,1)][1,min(n+m,1)][1,min(n+m,1)]范围内的点.求路径长度恰好为kkk的简单路径(一个点最多走一次)数. 1≤n ...
- Codeforce Round #554 Div.2 C - Neko does Maths
数论 gcd 看到这个题其实知道应该是和(a+k)(b+k)/gcd(a+k,b+k)有关,但是之后推了半天,思路全无. 然而..有一个引理: gcd(a, b) = gcd(a, b - a) = ...
随机推荐
- Java基础(四) StringBuffer、StringBuilder原理浅析
StringBuilder与StringBuffer作用就是用来处理字符串,但String类本身也具备很多方法可以用来处理字符串,那么为什么还要引入这两个类呢? 关于String的讲解请看Java基础 ...
- 开源|性能优化利器:数据库审核平台Themis的选型与实践
作者:韩锋 出处:DBAplus社群分享:来源:宜信技术学院 Themis开源地址:https://github.com/CreditEaseDBA 一.面临的挑战 1.运维规模及种类 我相信,这也是 ...
- Swift的访问控制讲解
Swift中访问修饰符总共有5种,分别为fileprivate,private,internal,public和open,其中,fileprivate以及open是Swift 3新添加的.因为过去的S ...
- spring 5.x 系列第20篇 ——spring简单邮件、附件邮件、内嵌资源邮件、模板邮件发送 (代码配置方式)
源码Gitub地址:https://github.com/heibaiying/spring-samples-for-all 一.说明 1.1 项目结构说明 邮件发送配置类为com.heibaiyin ...
- 最全java多线程总结3——了解阻塞队列和线程安全集合不
看了前两篇你肯定已经理解了 java 并发编程的低层构建.然而,在实际编程中,应该经可能的远离低层结构,毕竟太底层的东西用起来是比较容易出错的,特别是并发编程,既难以调试,也难以发现问题,我们还是 ...
- 【JVM】虚拟机初见-运行时数据区图解
本文是听咕泡XX公开课视频整理的笔记,较书本更为总结,感谢. 计算机模型(汇编知识):数据集(数据).指令集(操作指令,+-等).控制集(分支循环) JVM运行时的数据区: 程序计数器(每个线程都有) ...
- java中关于IO流的知识总结(重点介绍文件流的使用)
今天做软件构造实验一的时候,用到了java文件流的使用,因为之前学的不是很踏实,于是决定今天好好总结一下, 也方便以后的回顾. 首先,要分清IO流中的一些基础划分: 按照数据流的方向不同可以分为:输入 ...
- Linux上安装Nginx依赖环境和库、Nginx安装,Nginx服务命令
安装Nginx依赖环境和库.Nginx安装,Nginx服务命令 因为Nginx官方提供的是C源码,要自己进行编译,所以需要自己拥有编译所依赖的环境和库才可正常编译 安装gcc yum -y insta ...
- [乐意黎原创]Centos 7里apache(httpd)自启动
最近,Aerchi在折腾 ECS服务器 (Centos 7),每次重启后都要手动开启apache服务,好繁琐. 仔细研究了下:Apache 的服务第一.启动.终止.重启systemctl start ...
- iOS 矢量图pdf替换2倍3倍图
一.在开发中矢量图的使用大大提高设计的切图效率! ios 中可以用pdf替换现在的2倍3倍图(1倍图已经忽略) 1.将pdf矢量图拖进工程Assets.xcassets中 2.按照步骤操作 3.矢量图 ...