topcoder srm 662 div1

problem1 link

首先枚举差值$d$，判断是否存在一个序列任意连续两个之间的差值小于$d$。

首先将数字排序，然后从小到大依次放置每一个数字。每个当前的数字有两个位置可以放，当前序列的前面或者后面。设当前序列开始末尾的两个数字为$L,R$，当前数字为$x$。

如果$x-L>d$并且$x-R>d$，那么不存在这样的序列。

如果$x-L\leq d$并且$x-R\leq d$，那么开始末尾都可以放。这时候按照贪心的思路，应该放在$L,R$小的一侧。

否则，只能放在某一侧。

problem2 link

令$f[k][t]$表示$k$个节点构成的树$T_{k}$满足$S(T_{k})$%$m=r$的最小的$S(T_{k})$。合并两棵树时有转移方程:$f[k][t]=f[x][t_{0}]+f[k-x][t_{1}]+x(n-x),t=(t_{0}+t_{1}+x(n-x))(mod)(m)$。

如果对于上图来说，集合$C$中还有的结点数为$n-5$。

那么$f[5][t]=f[3][t_{0}]+f[2][t_{1}]+3(n-3)$。其中$f[5][t]$中包含了内部５个结点任意两个之间的距离，以及每个结点到外面的$n-5$个结点的距离中到结点４的这一段距离。所以$f[5][t]$包含了以下几段：

$1\leftrightarrow 3,1\leftrightarrow 2,1\leftrightarrow 4,1\leftrightarrow 5$
$3\leftrightarrow 2,3\leftrightarrow 4,3\leftrightarrow 5$
$2\leftrightarrow 4,2\leftrightarrow 5$
$4\leftrightarrow 5$
$(n-5)(1\leftrightarrow 4)$
$(n-5)(3\leftrightarrow 4)$
$(n-5)(2\leftrightarrow 4)$
$(n-5)(4\leftrightarrow 4)$
$(n-5)(5\leftrightarrow 4)$

problem3 link

首先定义给定的运算为$g(a,b)=a*b$，另外定义$f(x)=g(0,x)$.所以如果$g(0,0)=3\rightarrow g(3,x)=g(g(0,0),x)=g(0,g(0,x))=g(0,f(x))=f(f(x))=f^{2}(x)$。如果将给定的输入$a[0,1,..,n-1]$看作是一棵树(即如果$a[i]=j$，那么有一条$i$到$j$的有向边),那么$f^{k}(x)$表示从节点$x$向下走$k$步到达的节点。

首先假设有一棵如下的树：

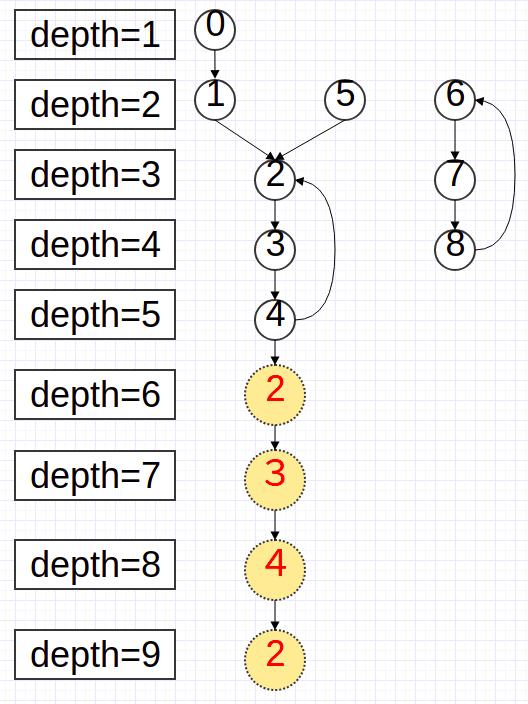
令节点0 到环的距离为$m=2$,０所在的联通分量的环的大小为$c=3$。那么有对于任意的节点$x$，一定满足$f^{k}(x)=f^{k+c}(x),k\geq m+1$

所以以下两种情况是无解的：

（１）存在另外一个大小为$p$的环，但是$p$不能整除$c$。比如下图，有$(0*0)*4=g(1,4)=f^{2}(4)=4,(0*0*0*0*0)*4=g(1,4)=f^{5}(4)=5$，矛盾。

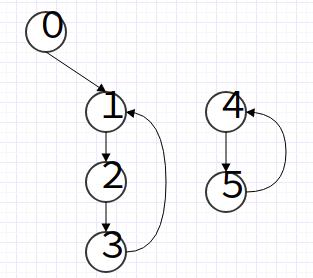
（２　存在一个节点，到达环的距离大于$m+1$.如下图。那么有$(0*0)*4=g(2,4)=0,(0*0*0*0)*4=g(2,4)=3$矛盾。

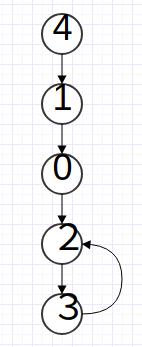
除了以上情况，都是存在解的。解的构造分两种情况：

（１）跟０不在一个联通分量中的节点$x$,有$g(x,t)=x$

（２）跟０在一个联通分量中的节点$x$，首先计算一个深度数组$d$,其中$d_{0}=1$，如果有边$i$到$j$，那么有$d_{j}=d_{i}+1$。那么$g(x,y)=f^{d_{x}}(y)$.

由此得到的转移数组$g$，满足对任意的三个数字$a,b,c$，满足$g(g(a,b),c)=g(a,g(b,c))$

分两种情况说明：

（１）$a,b,c$中前两个数字存在至少一个点跟０不在一个联通分量中，如果是$a$，那么有$g(g(a,b),c)=g(a,g(b,c))=a$,如果是$b$，那么有$g(g(a,b),c)=g(a,g(b,c))=g(a,b)=f^{d_{a}}(b)$
（２）$a,b,c$中前两个数字都跟０在一个联通分量中。那么$g(g(a,b),c)=g(a,g(b,c))=f^{d_{a}+d_{b}}(c)$.最后都会走到一个深度为$d_{a}+d_{b}+d_{c}$的节点.比如在最上面的图中，令$(a,b,c)=(1,2,5)$，那么$g(g(1,2),5)=g(4,5)=3,g(1,g(2,5))=g(1,4)=3$,可以看作是深度为$8$的节点

code for problem1

#include <algorithm>
#include <list>
#include <vector>

class FoxesOfTheRoundTable {
 public:
  std::vector<int> minimalDifference(const std::vector<int> &h) {
    int n = static_cast<int>(h.size());
    std::vector<std::pair<int, int>> a(n);
    for (int i = 0; i < n; ++i) {
      a[i] = {h[i], i};
    }
    std::sort(a.begin(), a.end());
    std::list<int> result;
    auto Check = [&](int kmax) {
      result.clear();
      result.push_back(a[0].second);
      for (int i = 1; i < n; ++i) {
        int first = h[result.front()];
        int last = h[result.back()];
        int current = a[i].first;
        if ((current - first <= kmax) && (current - last) <= kmax) {
          if (current - first > current - last) {
            result.push_front(a[i].second);
          } else {
            result.push_back(a[i].second);
          }
        } else if (current - first <= kmax) {
          result.push_front(a[i].second);
        } else if (current - last <= kmax) {
          result.push_back(a[i].second);
        } else {
          return false;
        }
      }
      return std::abs(h[result.front()] - h[result.back()]) <= kmax;
    };
    for (int d = 0; d < 1000; ++d) {
      if (Check(d)) {
        break;
      }
    }
    return {result.begin(), result.end()};
  }
};

code for problem2

#include <vector>

class ExactTree {
 public:
  int getTree(int n, int m, int r) {
    std::vector<std::vector<int>> f(n + 1, std::vector<int>(m, -1));
    f[1][0] = 0;
    for (int k = 2; k <= n; ++k) {
      for (int x = 1; x < k; ++x) {
        for (int t0 = 0; t0 < m; ++t0)
          for (int t1 = 0; t1 < m; ++t1) {
            if (f[x][t0] != -1 && f[k - x][t1] != -1) {
              int r = (f[x][t0] + f[k - x][t1] + x * (n - x)) % m;
              int s = f[x][t0] + f[k - x][t1] + x * (n - x);
              if (f[k][r] == -1 || s < f[k][r]) {
                f[k][r] = s;
              }
            }
          }
      }
    }
    return f[n][r];
  }
};

code for problem3

#include <vector>

class MultiplicationTable {
 public:
  std::vector<int> getMultiplicationTable(const std::vector<int> &a) {
    int n = static_cast<int>(a.size());
    std::vector<int> result(n * n, -1);
    auto Get = [&](int x, int y) { return result[x * n + y]; };
    auto Set = [&](int x, int y, int t) { result[x * n + y] = t; };

    std::vector<int> d(n, -1);
    for (int x = 0, depth = 1; d[x] == -1; ++depth) {
      d[x] = depth;
      x = a[x];
    }
    bool stop = false;
    while (!stop) {
      bool update = false;
      for (int i = 0; i < n; ++i) {
        if (d[i] == -1 && d[a[i]] != -1) {
          d[i] = d[a[i]] - 1;
          update = true;
          if (d[i] == -1) {
            stop = true;
            break;
          }
        }
      }
      if (!update || stop) {
        break;
      }
    }
    for (int i = 0; i < n; ++i) {
      if (d[i] == -1) {
        for (int j = 0; j < n; ++j) {
          Set(i, j, i);
        }
      } else {
        for (int j = 0; j < n; ++j) {
          int current = j;
          for (int k = 0; k < d[i]; ++k) {
            current = a[current];
          }
          Set(i, j, current);
        }
      }
    }

    for (int i = 0; i < n; ++i) {
      for (int j = 0; j < n; ++j) {
        for (int k = 0; k < n; ++k) {
          if (Get(Get(i, j), k) != Get(i, Get(j, k))) {
            return {-1};
          }
        }
      }
    }
    return result;
  }
};