#2718. 「NOI2018」归程 kruskal重构树

链接

https://loj.ac/problem/2718

思路

我们希望x所在的连通块尽量的大，而且尽量走高处

离线的话可以询问排序，kruskal过程中更新答案

在线就要用kruskal重构树

这kruskal重构树的话，看图就明白了

叶子节点都是原树节点

非叶子节点都是边

按照从大到小的顺序依次加边(是深度不是长度)

如果连通块已经在一起就不联通，其他两个最大节点和这个边(新建节点)连边

看图就是很明白



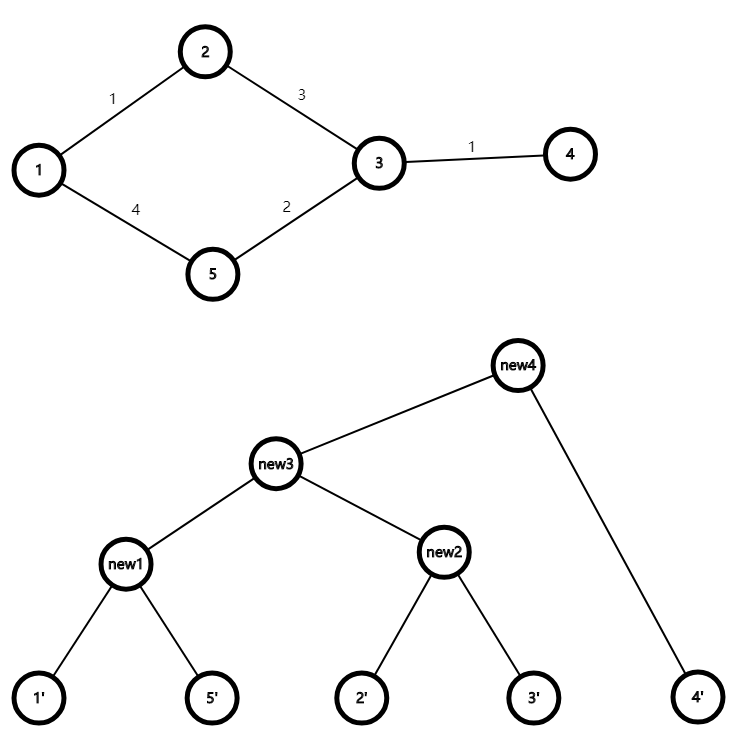
我们发现，重构树的根到任意节点是单调的，也就是说，这是个二叉堆啊

那两点间联通的最小需要深度就是lca(x,y)这条边的深度

询问就是s这个点最远能向上跳到的最远点的子树答案

可能我讲的听不懂，那就看图自己想想吧

复杂度最多一个log

大体流程

多组数据，进入solve

dij预处理dis

kruskal利用并查集重构出树来

lca树剖预处理重构树

再dfs统计子树ans

之后在线查询lca

输出lca这个点的ans

细节

并查集最好优化下，因为他重构出来的树很容易感觉成哈夫曼树的形状

并查集按秩合并和随机rand时间差别不大

树剖链外跳，链内二分

错误

写了比较慢、、(不过一遍60TLE还是很嗨的)

错误只有一个，dij的堆忘记了默认大顶堆，导致复杂度不对，T死了

代码

/*
大体流程：
多组数据，进入solve
dij预处理dis
kruskal重构出树来
lca树剖预处理重构树(其实就是二分)
再dfs统计子树ans
之后在线查询
*/
#include <iostream>
#include <ctime>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <queue>
#include <utility>
#include <algorithm>
using namespace std;
const int N=1e6+7;
int read() {
	int x=0,f=1;char s=getchar();
	for(;s>'9'||s<'0';s=getchar()) if(s=='-') f=-1;
	for(;s>='0'&&s<='9';s=getchar()) x=x*10+s-'0';
	return x*f;
}
int n,m,rt;
int dis[N],w[N<<1],dsr[N<<1];
struct node {
	int u,v,l,a;
	bool operator < (const node &b) const {
		return a>b.a;
	}
} edge[N];
struct noi_2018_t1 {
	int v,nxt;
} e[N<<1];
int head[N<<1],add_tot;
void add(int u,int v) {
//	cout<<u<<" "<<v<<"\n";
	e[++add_tot].v=v;
	e[add_tot].nxt=head[u];
	head[u]=add_tot;
}
namespace bcj {
	int fa[N<<1],siz[N<<1],id[N<<1];
	int find(int x) {
		return fa[x]==x ? x : fa[x]=find(fa[x]);
	}
	void uu(int fx,int fy) {
		fx=find(fx),fy=find(fy);
		id[fx]=id[fy]=max(id[fx],id[fy]);
		if(siz[fx]<=siz[fy]) {
			fa[fx]=fy;
			if(siz[fx]==siz[fy]) siz[fy]++;
		} else {
			fa[fy]=fx;
		}
	}
}
namespace get_lca {
	int fa[N<<1],top[N<<1],siz[N<<1],son[N<<1],dep[N<<1],idx[N<<1],js,frm[N<<1];
	void dfs1(int u,int f) {
		dep[u]=dep[f]+1;
		fa[u]=f;
		siz[u]=1;
		for(int i=head[u];i;i=e[i].nxt) {
			int v=e[i].v;
			dfs1(v,u);
			siz[u]+=siz[v];
			if(siz[son[u]]<siz[v]) son[u]=v;
		}
	}
	void dfs2(int u,int topf) {
		top[u]=topf;
		idx[u]=++js;
		frm[js]=u;
		if(!son[u]) return;
		dfs2(son[u],topf);
		for(int i=head[u];i;i=e[i].nxt) {
			int v=e[i].v;
			if(!idx[v]) dfs2(v,v);
		}
	}
	int lca(int x,int val) {
		int ans=x;
		while(w[top[x]]>val) ans=top[x],x=fa[top[x]];
		int l=idx[top[x]],r=idx[x];
		while(l<=r) {
//			cout<<l<<" "<<r<<"\n";
			int mid=(l+r)>>1;
			if(w[frm[mid]]>val) ans=frm[mid],r=mid-1;
			else l=mid+1;
		}
		return ans;
	}
	void init() {
		dfs1(rt,0);
		dfs2(rt,rt);
	}
}
namespace dij {
	struct node {
		int v,nxt,q;
	}e[N<<1];
	int head[N<<1],tot;
	void add(int u,int v,int q) {
		e[++tot].v=v;
		e[tot].q=q;
		e[tot].nxt=head[u];
		head[u]=tot;
	}
	void dij() {
		priority_queue<pair<int,int> > q;
		q.push(make_pair(0,1));
		dis[1]=0;
		while(!q.empty()) {
			pair<int,int> u=q.top();
			q.pop();
			if(dis[u.second]!=-u.first) continue;
			for(int i=head[u.second];i;i=e[i].nxt) {
				int v=e[i].v;
				if(dis[v]>dis[u.second]+e[i].q) {
					dis[v]=dis[u.second]+e[i].q;
					q.push(make_pair(-dis[v],v));
				}
			}
		}
	}
	void work() {
		memset(dis,0x3f,sizeof(dis));
		memset(head,0,sizeof(head));
		tot=0;
		for(int i=1;i<=m;++i) {
			add(edge[i].u,edge[i].v,edge[i].l);
			add(edge[i].v,edge[i].u,edge[i].l);
		}
		dij();
	}
}
namespace kruskal {
	void work() {
		for(int i=1;i<n+n;++i) bcj::fa[i]=i;
		for(int i=1;i<n+n;++i) bcj::id[i]=i;
		sort(edge+1,edge+1+m);
		for(int i=1;i<=n;++i) w[i]=0x3f3f3f3f;
		for(int i=1,js=n;i<=m;++i) {
			int fx=bcj::find(edge[i].u),fy=bcj::find(edge[i].v);
			if(fx!=fy) {
				rt=++js;
				add(js,bcj::id[fx]),add(js,bcj::id[fy]);
				w[js]=edge[i].a;
				bcj::uu(js,fy);
				bcj::uu(js,fx);
				if(js==n+n-1) return;
			}
		}
	}
}
void clear() {
	add_tot=0;
	dij::tot=0;
	get_lca::js=0;
	memset(dij::head,0,sizeof(dij::head));
	memset(get_lca::siz,0,sizeof(get_lca::siz));
	memset(bcj::siz,0,sizeof(bcj::siz));
	memset(head,0,sizeof(head));
	memset(dis,0x3f,sizeof(dis));
	memset(get_lca::idx,0,sizeof(get_lca::idx));
	memset(get_lca::son,0,sizeof(get_lca::son));
}
void dfs(int u,int f) {
	dsr[u]=dis[u];
	for(int i=head[u];i;i=e[i].nxt) {
		int v=e[i].v;
		dfs(v,u);
		dsr[u]=min(dsr[u],dsr[v]);
	}
}
void solve() {
	dij::work();
	// cout<<"1\n";
	kruskal::work();
	// cout<<"2\n";
	get_lca::init();
	// cout<<"3\n";
	dfs(rt,0);
	int Q=read(),k=read();
	int S=read(),lastans=0;
	while(Q--) {
		int vv=read(),pp=read();
		int v=(vv+k*lastans-1)%n+1;
		int p=(pp+k*lastans)%(S+1);
		int tmp=get_lca::lca(v,p);
		lastans=dsr[tmp];
		printf("%d\n",lastans);
	}
}
int main() {
	freopen("return.in","r",stdin);
	freopen("return.out","w",stdout);
	int T=read();
	while(T--) {
		n=read(),m=read();
		for(int i=1;i<=m;++i) {
			edge[i].u=read(),edge[i].v=read();
			edge[i].l=read(),edge[i].a=read();
		}
		clear();
		solve();
	}
	return 0;
}