bzoj千题计划300：bzoj4823: [Cqoi2017]老C的方块

http://www.lydsy.com/JudgeOnline/problem.php?id=4823

讨厌的形状就是四联通图

且左右各连一个方块

那么破坏所有满足条件的四联通就好了

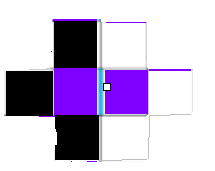
按上图方式染色之后，任意满足要求的四联通块一定可以是

黑色-->紫左-->紫右-->白色

只要破坏三个箭头中的一个即可

所以可以构建最小割模型

1、源点向黑色格连流量为格子代价的边

2、黑色格向相邻的紫色格连inf边

3、与黑色格相邻的紫色格向与白色格相邻的紫色格连 流量 为 两个紫色格较小代价 的边

4、与白色相邻的紫色格向白色格连inf边

5、白色格向汇点连流量为格子代价的边

染完之后长这样：

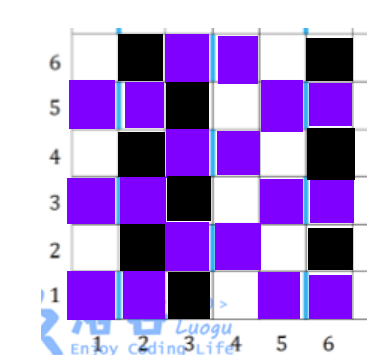
注意：

不要在枚举紫色格子的过程中连源点汇点的边

这样会导致连重边

比如这样黑色格子就会与源点有重边，两个紫色格子各贡献了一条边

但实际我们只能用一条边

所以可以标记哪些格子与源点、汇点有边，最后再连

（再次吐槽一次bzoj的题面~~）

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<map>
#include<queue>
 
using namespace std;
 
typedef long long LL;
 
#define N 100002
#define M 1400001
 
const int inf=2e9;
 
map<LL,int>mp;
 
int n,m,k;
int xi[N],yi[N],zi[N];
 
int front[N],nxt[M<<],to[M<<],cap[M<<],tot=;
int lev[N],cur[N];
int src,decc;
queue<int>q;
 
bool uses[N],uset[N];
 
void read(int &x)
{
    x=; char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)) { x=x*+c-''; c=getchar(); }
}
 
LL turn(int i,int j)
{
    return 1LL*(i-)*m+j;
}
 
void init()
{
    read(m); read(n); read(k);
    int y,x;
    for(int i=;i<=k;++i)
    {
        read(yi[i]); read(xi[i]); read(zi[i]);
        mp[turn(xi[i],yi[i])]=i;
    }
    decc=k+;
}
 
void add(int u,int v,int val)
{
    to[++tot]=v; nxt[tot]=front[u]; front[u]=tot; cap[tot]=val;
    to[++tot]=u; nxt[tot]=front[v]; front[v]=tot; cap[tot]=;
//    printf("%d %d %d\n",u,v,val);
}
 
void Add(int x,int l,int r,int y)
{
    if(y%== || !(y%))
    {
        uses[x]=true;
        add(x,l,inf);
    }
    else
    {
        uset[x]=true;
        add(r,x,inf);
    }
}
 
void build()
{
    int x,y;
    int tmp,l,r;
    int l1,l2,l3,r1,r2,r3;
    for(int i=;i<=k;++i)
    {
        x=xi[i]; y=yi[i];
        if(y==m) continue;
        if(((x&) && y%==) || (!(x&) && y%==))
        {
            tmp=mp[turn(x,y+)];
            if(!tmp) continue;
        }
        else continue;
        if(x>) l1=mp[turn(x-,y)]; else l1=;
        if(x<n) l2=mp[turn(x+,y)];    else l2=;
        if(y>) l3=mp[turn(x,y-)]; else l3=;
        if(!(l1||l2||l3)) continue;
        if(x>) r1=mp[turn(x-,y+)]; else r1=;
        if(x<n) r2=mp[turn(x+,y+)]; else r2=;
        if(y<n-) r3=mp[turn(x,y+)]; else r3=;
        if(!(r1||r2||r3)) continue;
        l=i; r=tmp;
        if(y%==) swap(l,r);
        add(l,r,min(zi[l],zi[r]));
        if(l1) Add(l1,l,r,yi[l1]);
        if(l2) Add(l2,l,r,yi[l2]);
        if(l3) Add(l3,l,r,yi[l3]);
        if(r1) Add(r1,l,r,yi[r1]);
        if(r2) Add(r2,l,r,yi[r2]);
        if(r3) Add(r3,l,r,yi[r3]);
    }
    for(int i=;i<=k;++i)
        if(uses[i]) add(src,i,zi[i]);
    for(int i=;i<=k;++i)
        if(uset[i]) add(i,decc,zi[i]);
}
 
bool bfs()
{
    while(!q.empty()) q.pop();
    for(int i=src;i<=decc;++i) lev[i]=-,cur[i]=front[i];
    lev[src]=;
    q.push(src);
    int now,t;
    while(!q.empty())
    {
        now=q.front();
        q.pop();
        for(int i=front[now];i;i=nxt[i])
        {
            t=to[i];
            if(lev[t]==- && cap[i])
            {
                lev[t]=lev[now]+;
                if(t==decc) return true;
                q.push(t);
            }
        }
    }
    return false;
}
 
int dinic(int now,int flow)
{
    if(now==decc) return flow;
    int rest=,delta,t;
    for(int &i=cur[now];i;i=nxt[i])
    {
        t=to[i];
        if(lev[t]>lev[now] && cap[i])
        {
            delta=dinic(t,min(flow-rest,cap[i]));
            if(delta)
            {
                cap[i]-=delta;
                cap[i^]+=delta;
                rest+=delta;
                if(rest==flow) break;
            }
        }
    }
    if(rest!=flow) lev[now]=-;
    return rest;
}
 
void solve()
{
    int ans=;
    while(bfs()) ans+=dinic(src,inf);
    printf("%d",ans);
}
 
int main()
{
    freopen("data.in","r",stdin);
    freopen("my.out","w",stdout);
    init();
    build();
    solve();
}